Оглавление:
Производная по направлению
Для характеристики скорости изменения поля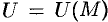 
в заданном направлении введем понятие «производной по направлению».
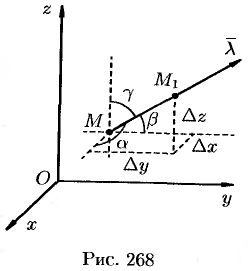
Возьмем в пространстве, где задано поле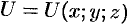 
, некоторую точку 
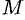и найдем скорость изменения функций 
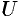при движении точки 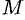в произвольном направлении 
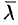. Пусть вектор 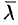имеет начало в точке 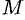и направляющие косинусы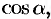 
.
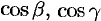Приращение функции 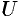, возникающее при переходе от точки 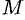к некоторой точке 
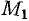в направлении вектора 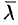определяется как
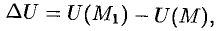
или
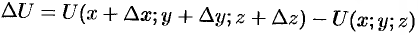
(см. рис. 268). Тогда
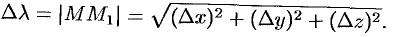
Производной от функции 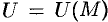в точке 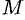по направлению 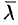называется предел
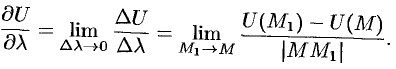
Производная по направлению 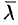и характеризует скорость изменения функции (поля) в точке 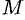по этому направлению. Если 
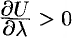, то функция 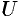возрастает в направлении 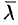, если 
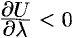, то функция 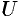в направлении 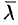убывает. Кроме того, величина 
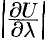представляет собой мгновенную скорость изменения функции 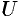в направлении 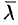в точке 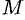: чем больше 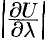, тем быстрее изменяется функция 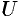. В этом состоит физический смысл производной по направлению.
Выведем формулу для вычисления производной по направлению, считая, что функция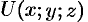 
дифференцируема в точке 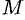. Тогда ее полное приращение в этой точке 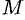можно записать так:
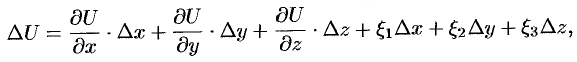
где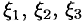 
— бесконечно малые функции при 
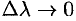(см. п. 44.3).
Поскольку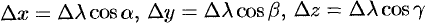 
, то
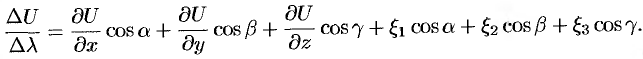
Переходя к пределу при 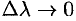, получим формулу для вычисления производной по направлению:
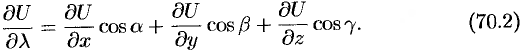
В случае плоского поля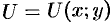 
имеем: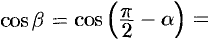 
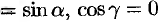. Формула (70.2) принимает вид:
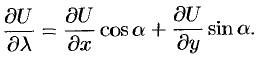
Замечание. Понятие производной по направлению является обобщением понятия частных производных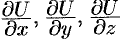 
. Их можно рассматривать как производные от функции 
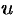по направлению координатных осе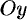й 
, 
и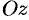 
. Так, если направление 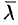совпадает с положительным направлением оси , то, положив в формуле (70.2)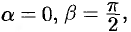 
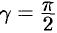, получим 
.
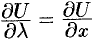Пример №70.1.
Найти производную функции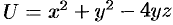 
в точке 
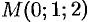в направлении от этой точки к точке 
.
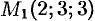Решение:
Находим вектор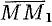 
и его направляющие косинусы:
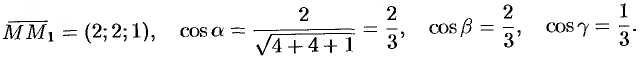
Находим частные производные функции и вычисляем их значения в точке :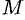
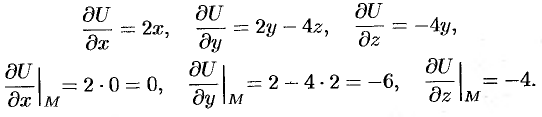
Следовательно, по формуле (70.2) имеем:
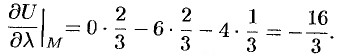
Поскольку 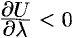, то заданная функция в данном направлении убывает.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Разложение в ряд фурье периодических функций с периодом 2п |
| Поверхности и линии уровня скалярного поля |
| Векторные линии поля |
| Поток векторного поля |
