Пусть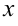 
— начальное значение независимой переменной, 
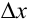— приращение, 
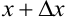— приращённое значение независимой переменной. Тогда 
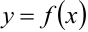— начальное значение функции, 
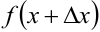— приращённое значение функции, 
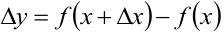— приращение функции, соответствующее приращению аргумента .
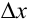Производной функции 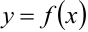называется предел отношения приращение функции к приращению аргумента, при стремлении последнего к нулю:
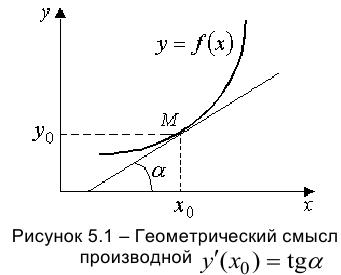
Геометрический смысл производной: производная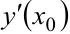 
численно равна тангенсу угла наклона касательной к графику функции, проведенной через точку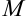 
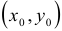, где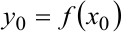 
(см. рисунок 5.1).
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
| Эквивалентные бесконечно малые величины: теоремы и таблица |
| Непрерывность функции |
| Производная. Геометрический смысл производной |
| Правила дифференцирования и таблица производных основных функций |
