Производная суммы, разности, произведения и частного функций
Нахождение производной функции непосредственно по определению часто связано с определенными трудностями. На практике функции дифференцируют с помощью ряда правил и формул.
Пусть функции 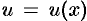 и
и 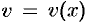 — две дифференцируемые в некотором интервале
— две дифференцируемые в некотором интервале 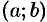 функции.
функции.
Теорема 20.2. Производная суммы (разности) двух функций равна сумме (разности) производных этих функций: 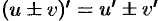 .
.
Обозначим 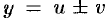 . По определению производной и основным теоремам о пределах получаем:
. По определению производной и основным теоремам о пределах получаем:
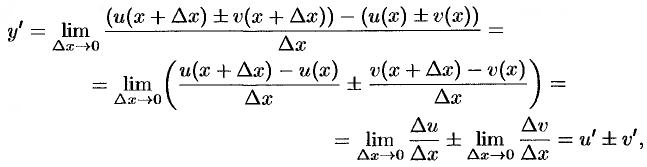
т. е. 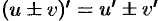 .
.
Теорема справедлива для любого конечного числа слагаемых.
Теорема 20.3. Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго: 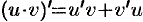 .
.
Пусть 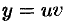 . Тогда
. Тогда
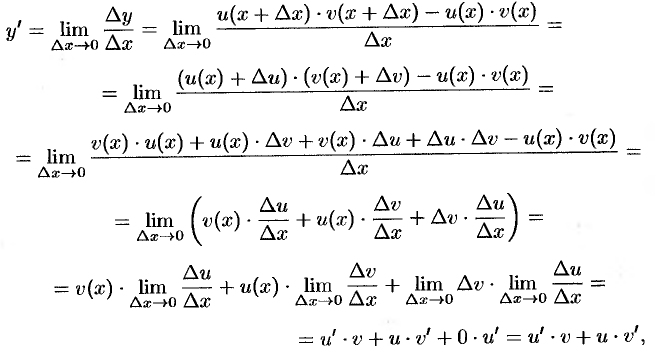
т. е. 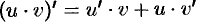 .
.
При доказательстве теоремы использовалась теорема о связи непрерывности и дифференцируемости: так как функции 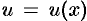 и
и 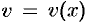 дифференцируемы, то они и непрерывны, поэтому
дифференцируемы, то они и непрерывны, поэтому  и
и 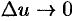 при
при 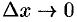 .
.
Можно показать, что:
а) 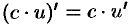 , где
, где 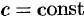 ;
;
б) 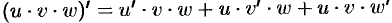 .
.
Теорема 20.4. Производная частного двух функций 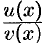 , если
, если 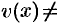
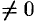 равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя:
равна дроби, числитель которой есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя: 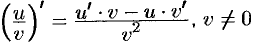 .
.
Пусть 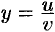 . Тогда
. Тогда
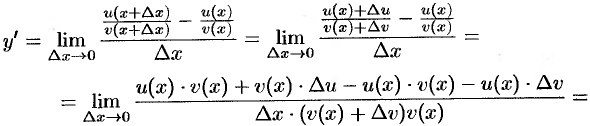
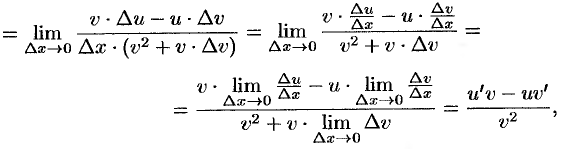
т.е. 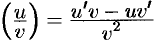 .
.
Следствие 20.1. 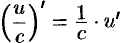 .
.
Следствие 20.2. 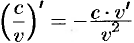 , где
, где 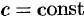 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Касательная к кривой |
| Связь между непрерывностью и дифференцируемостью функции |
| Производная сложной и обратной функций |
| Гиперболические функции и их производные |

