Оглавление:
Производная функции, заданной параметрически
Пусть зависимость между аргументом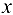 
и функцией 
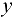задана параметрически в виде двух уравнений
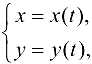
где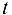 
— параметр.
Найдем производную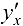 
считая, что функции (5.10) имеют производные и что функция 
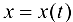имеет обратную 
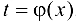. По правилу дифференцирования обратной функции
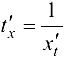
Функцию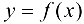 
, определяемую параметрическими уравнениями (5.10), можно рассматривать как сложную 
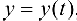функцию , где 
.
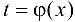По правилу дифференцирования сложной функции имеем
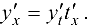
С учетом равенства (5.11) получаем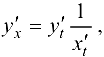 
, т. е.
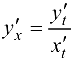
Формула (5.12) позволяет находить производную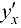 
, от функции заданной параметрически, не находя зависимость 
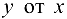в явном виде.
Пример 5.12.
Пусть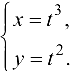 
Найти .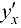
Решение:
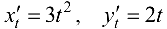
поэтому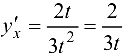 
.
Если непосредственно найти зависимость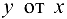 
, то получим
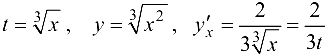
Ответ: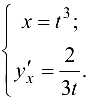 
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:
| Производная обратной функции с примерами решения |
| Производная функции, заданной неявно с примерами решения |
| Логарифмическая производная с примером решения |
| Производные высших порядков с примером решения |
