Оглавление:
Производная, ее геометрический и физический смысл
Пусть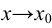 
, тогда 
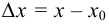— приращение аргумента. Рассмотрим функцию 
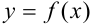, заданную в промежутке 
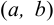. Пусть 
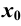и 
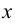принадлежат 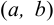, тогда приращение функции в точке 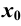выразится формулой:
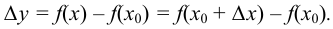
Рассмотрим предел
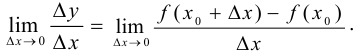
Если он существует и конечен, то его называют производной функции 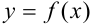в точке .
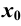Производную функции 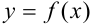в точке 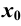обозначают символом 
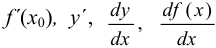. Следовательно, по определению
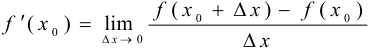или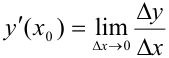 
.
Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Она будет и непрерывной. Операция нахождения производной называется дифференцированием.
Геометрический смысл производной
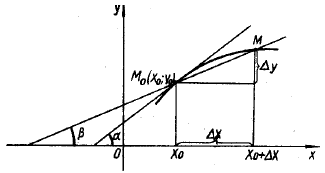
Из рисунка видно, что геометрический смысл производной выражается формулой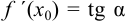 
, т. е. производная от данной функции в данной точке 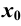равна тангенсу угла между осью 
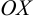и касательной к графику этой функции в соответствующей точке:
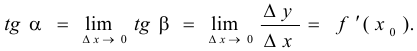
Формула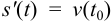 
выражает физический смысл производной: производная от пути по времени равна скорости прямолинейного движения точки.
Правила и формулы дифференцирования. Производная сложной функции
Если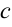 
— постоянное число и 
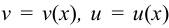— некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
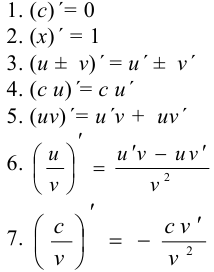
Если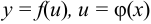 
, т. е. 
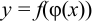— сложная функция, составленная из дифференцируемых функций, то 
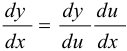или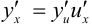 
.
На основании определения производной и правил дифференцирования можно составить таблицу производных элементарных функций:
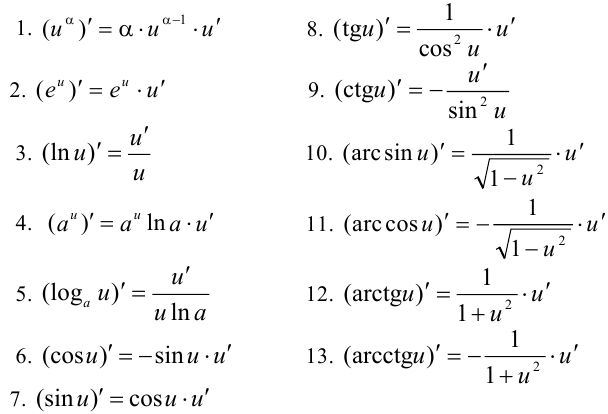
Задача №48.
На основании определения производной вывести формулу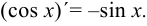 
Решение:
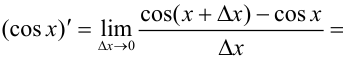
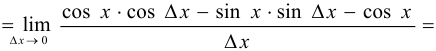
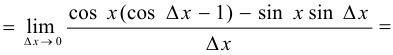
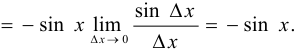
Задача №49.
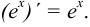
Решение:
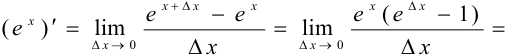
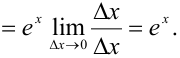
Задача №50.
Найти производную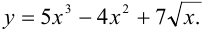 
Решение:
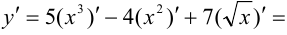
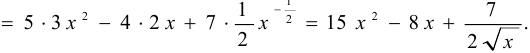
Задача №51.
Найти производную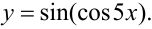 
Решение:
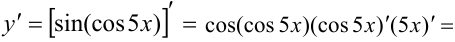
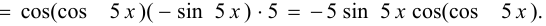
Задача №52.
Найти производную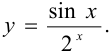 
Решение:
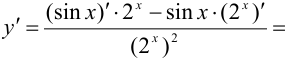
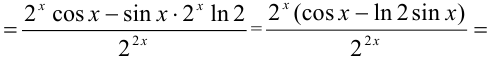
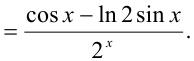
Задача №53.
Найти производную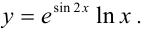 
Решение:
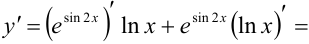
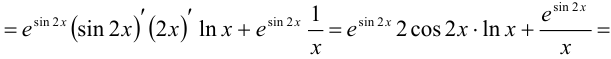
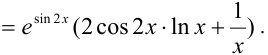
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
