Производная и её вид

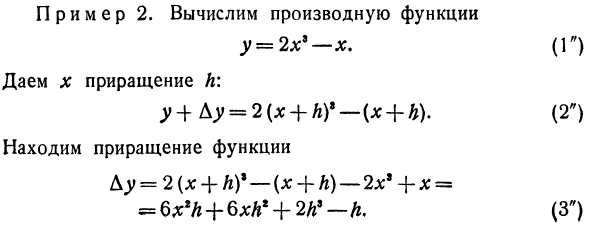
Производная

• производная В предыдущем параграфе мы рассмотрели два разных примера, но между ними есть что-то общее. Чтобы найти его, вам нужно взять функциональную перспективу. Предположим, что задана функция g- * (*). Чтобы получить проблему со скоростью, предположим, что независимой переменной x является время, а y — расстояние точки, движущейся по прямой линии от начала координат. Уравнение y = zf (x) в этом случае htf (x + h) J Чай называется законом движения.

. Для касательных задач это означает, что мы определили координаты точки на кривой, определяемой уравнением y = f (x) (рис. 48). 2. Дайте x приращение h и вычислите соответствующее значение приращения y>. Это разница между исходным значением и значением Du (приращение функции) (гл. V, см. §4). y + by = f (xih).

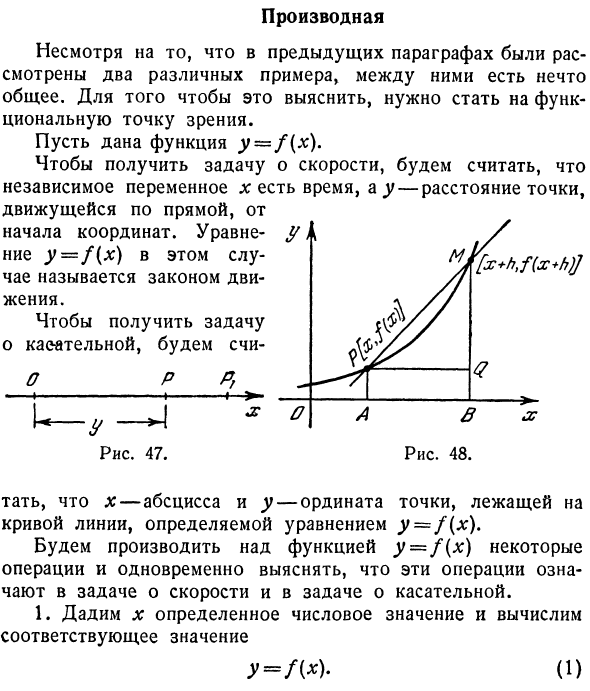
Для вопросов скорости это означает, что в определенный момент x мы нашли расстояние ^ от движущейся точки от начала координат (рисунок 47) Людмила Фирмаль

(2)Рассчитать, чтобы получить касательную проблему р о -h- p, f Рисунок 47. Кроме того, x — абсцисса, а y — ордината точки на кривой, определяемой уравнением y = f (x). Выполните несколько операций с функцией y == / (x) и одновременно выясните, что эти операции означают для задач со скоростью и касательной. 1. Дайте х конкретное число и рассчитайте соответствующее значение Y = f (x). (1)

Для проблемы скорости он определил положение Px движущейся точки в момент времени x-j-h. В касательной задаче получена новая точка G, где AB = PQ = / r, OB = x + h, BM = f (x + h). 3. Найдите приращение функции Du. Поэтому вычтите член (1) из члена (2). D * = / (* + A) — / (*). (3) Для вопросов скорости вычисляется расстояние, пройденное точкой в ​​интервале времени от времени x до времени x + h. Для касательных задач вычисляется отрезок QM-BM — BQ = BM-AP. 4. Разделите Dy на A.

• То есть найдите отношение приращения функции к приращению независимой переменной. Y y_f (x + h) -f (x) h-h ‘w Для вопросов скорости вычисляется средняя скорость для временного интервала h от времени x до времени l + A. В задаче касательной находится тангенс угла QPM, который представляет собой отношение отрезков QM и PQ, то есть коэффициент угла секущей RM. 5. Найти предел в условиях h —► (). ч- * о * л-о ч ^ Для проблем со скоростью обнаруженный предел указывает скорость в определенный момент. Для касательных задач это ограничение дает тангенс угла наклона касательной для оси оса.

Таким образом, последовательность операций 1, 2, 3, 4 и 5, выполняемых над функцией, приводит к двум важным понятиям. 1) Текущая скорость, 2) Угловой коэффициент тангенса. Однако эти два приложения не будут исчерпаны указанной последовательностью операций. Поэтому рекомендуется рассмотреть последовательность операций p, рассмотренную в общем виде. Для этого сначала определите это.

Производная функции определения f (x) является пределом отношения приращения функции к приращению независимой переменной, при условии, что приращение независимой переменной стремится к нулю. Или у, или около того: f (x) = y ′ = dJL = lim lim fJH ± Jpm. J v » d * th-оФft-o h Пример 1. Вычислить производную функции у = (G) Для этого дайте х приращение h. y + & y = {x + hf. (2 ‘)

Производная функции y = f (x) обозначается через f ‘(x). / ду Людмила Фирмаль

Найти приращение функции A y. по = (x + h) t — xt = 2xh + tf. (3 ‘) Я ищу отношение приращения функции к приращению независимой переменной. х + ч (4 ‘) Найти предел этого отношения при условии h —► (). lim lim (2x + h) = 2x. (5 ‘) ч- + оо Таким образом, производная функции jt2 найдена. (Je2) ‘= 2x.Пример 2. Вычисление производной функции у = 2х9 —х. Дайте х приращение h: Найти приращения функции Au = 2 (x + h)% — (x + K) -2x * + l: =

Ищу отношение 22 = 6hg + 6 xh + 2L1-1. (4 «) Найти предел этого отношения, т.е. производную lim ^ = lim (bxr + & xh + 2h * -1) = 6x «-1. (5») X- + ч так (2×9-x) ‘= 6xg-1. Как видно из приведенного выше примера, вычисление производной довольно утомительно, но однообразно. Поэтому мы предпочитаем предварительно вычислять производные часто встречающихся функций, запоминать эти производные и использовать готовые результаты при решении задач.

Смотрите также:

Предмет высшая математика

Скорость	Правила вычисления производных
Касательная	Простейшие применения производной