Произведение множеств. График отображения

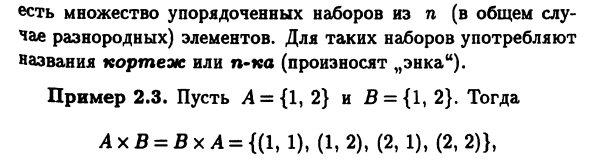
Произведение множеств. График отображения

• Напомним, что эти два перпендикулярны друг другу Оси с одинаковым масштабом Установите y-плоскость для обеих осей Прямоугольный декартов Координатная тема (рисунок 2.7). точка О пересечении координатных осей Называется происхождение. 1P в М Каждая точка М Совпадение пары (w, y) Реальное x, j / 6R, где x — координата точки Mx на оси координат Ox, y — координата точки Mu на оси координат Ox Координатная ось Oy. Точки Mx и Mu являются базами Вертикальные линии опущены из каждой точки М Оси ах и ах.

Числа x и y называются координатами Точка M (в выбранной системе координат) и x называются Абсцисса точки М и ордината у этой точки. Число с координатами. И наоборот, каждая точка М Плоскость соответствует реальной паре (а, 6) а И 6. В общем случае пары (а, б) и (&, а) определяются по-разному Укажите, в основном, какое из двух чисел а и 6 Пара указывается первой. Так что это О модифицированной паре. В связи с этим пара (а, б) и (6, а) Рассмотрим равенство между собой, и они определяют одно и то же Точка на плоскости, если a = b.

Очевидно, каждая пара действительных чисел (а, 6) a, 6 € R соответствует точке M с ними на плоскости. Людмила Фирмаль

Набор всех пар вещественных чисел и Множество точек на плоскости R2. Данная спецификация актуальна Прямая концепция (или Декартово) множество произведений (часто просто говорящих Набор продуктов). Определение 2.2. Произведение множеств A и B Вызывается набор Ах с возможными парами заказа (X, y), потому что первый элемент взят из A, а второй элемент взят из B, какие AxB = {(x, y): xeA, y € B}. Эквивалентность двух пар (x, y) и (xf, y ′) зависит от условия х = х1 и у = у *. Пара (x, y) и (y, x) считаются разными, Для хфу. Это особенно важно иметь в виду, когда: А и Б одинаковы. Так что в общем случае AxBfBxA, то есть Произвольный набор продуктов не является коммутативным,

Распространение о союзах и перекрестках И разница установлена: A x (BBC) = (A x B) D (A x C), O представляет одну из трех названных операций. Продукт набора Эти операции выполняются в двух наборах. результат Элементы, которые выполняют эти операции: Принадлежит одному или обоим оригинала (если не пустой) Set. Элементы набора продуктов Принадлежит к новому набору и является еще одним объектом Род по сравнению с элементом оригинального набора. Вы можете ввести понятия, как в определении 2.2. Более 3 комплектов. Установите (A x B) x C и L-x (B x C) идентифицируется и просто обозначается как A x B x C. Вот так A x B x C = {(i, y, z): x∈A, y∈B, z∈C}.

• Работа ах ах ах ах и другие методы показаны Обычно плоскость R2 четко проходит через A2, A3 и т. Д. Можно рассматривать как произведение двух копий R x R Набор действительных чисел (отсюда Укажите набор точек плоскости как произведение двух Набор числовых линий). Много очков Геометрическое (3D) пространство поддерживается Три копии набора R x R x R продукт-точек Линия обозначена R3. n наборов продуктов Действительное число указывает на Rn. Этот набор набор всех видов из n (xi, Xg »•••» & n) Действительные 2i, & 2, •• >> 2n G R и любая точка x * из Rn такой набор действительных чисел (x |, sj »•••) ^ n) XB X2> * ••) xn € R »произведение любого множества n Есть много упорядоченных множеств из n (как правило,

Для разных элементов). Использование такого набора Название поезда или партии (произносится как энка). Пример 2.3. Пусть A = {1, 2} и B = {1, 2}. тогда AxB = BxA = {(1, 1), (1, 2), (2, 1), (2, 2)}, и набор Ax B можно определить по 4 точкам Плоскость R2, координаты которой указаны в перечислении Элементы этого набора. Если C = {1, 2} и D = {3, 4} = {(L, 3), (1,4), (2,3), (2,4)}, £> xC = {(3,1), (3,2), (4,1), (4,2)}. Пусть пример 2.4 И F = {х: тогда = {(Xyy): Геометрическая интерпретация множеств E x F и F x E 2.8 показано на рисунке. # Mapping /: для X- + Y вы можете создать набор Упорядоченное подмножество (i, y) Прямой продукт X xY.

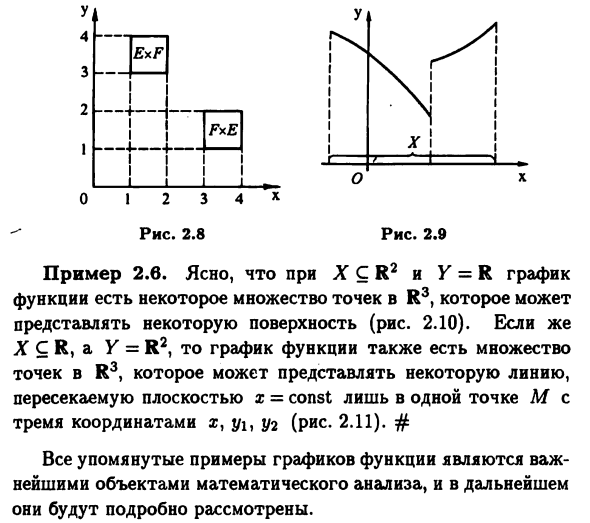
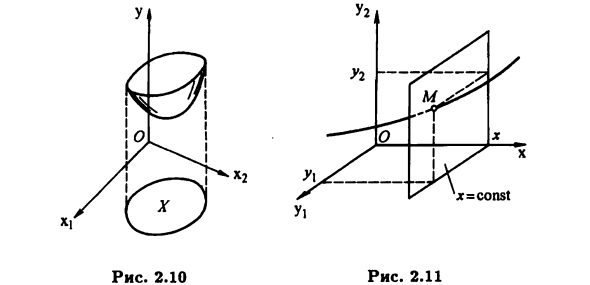
Такое множество Γ Отображение графа f (или граф функции называется Пример 2.5 Когда X C R и Y = R Упорядоченная пара определяет координаты точки на плоскости R2. В случае Этот X является интервалом числовой линии R. Графики функций могут представлять линии (рисунок 2.9).

Смотрите также:

Предмет математика

Обратное отображение	Упорядоченные множества. Элементы комбинаторики
Композиция отображений	Ограниченные множества