Оглавление:



Прохождение переменного тока по плоской шине (электрический поверхностный эффект)
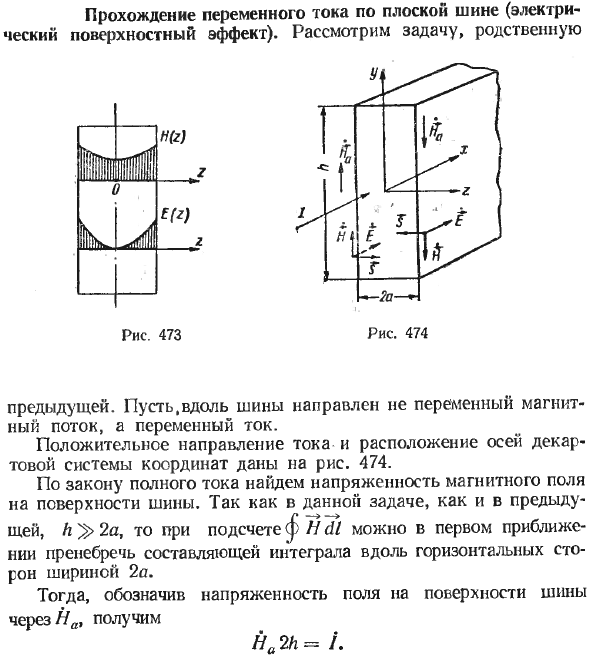
Прохождение переменного тока по плоской ванне (электрический поверхностный эффект). Рассмотрим вопросы, связанные с предыдущей проблемой.
- Вместо переменного магнитного потока он индуцирует переменный ток вдоль шины. На рисунке показано положительное направление тока и положение осей в декартовой системе координат. 474. Согласно закону полного тока,
напряженность магнитного поля на поверхности шины может быть определена. Людмила Фирмаль
В этой задаче h> 2a, как и в предыдущем примере, поэтому при расчете <£ H cP первое приближение может игнорировать интегральную составляющую вдоль горизонтального края ширины 2a. Затем, если напряженность электрического поля на поверхности шины выражается как // d, получается Na 2h = i.
Поэтому при составлении уравнения для определения постоянной интегрирования следует учитывать, что натяжение на левой стороне шины ориентировано вдоль положительного направления оси y и вправо в отрицательном направлении оси y.
- Общее решение для плоских волн d = 0 ^ 4-6 ^ — ^. Константа интегрирования: Когда r == — a ya = C.е ^ + С ^ и r = a, zJk получается путем решения двух последних уравнений одновременно. Замените 2sh pa C2 на общее решение. // _ n sh rg j sh rg 1 a- • sh pa * 2h sh pa
Напряженность поля £ направлена вдоль оси x и в точке пластины плотности тока, равной предыдущему Y dz или р7 chргY 2 / i shra i fc- / chpz 6 = yE = p-. Минимальное значение плотности тока 1 2 / i sh pa находится в центральной плоскости шины при z = 0, и
на графике показано изменение модуля II в зависимости от z. 475. Людмила Фирмаль
Вторая кривая показана на том же рисунке и показывает зависимость коэффициента плотности тока от r. Вы можете видеть, что кривая 473 на рисунке 475, график изменения E и H из-за электрических и магнитных поверхностных эффектов, кажется, меняет местоположение. Чем толще ванна, тем больше y, p и co, и тем сильнее поверхностный эффект.
Другими словами, распределение плотности тока по сечению шины неоднородно. Если частота с очень высока, можно обнаружить, что ток течет только через тонкий поверхностный слой шины. Если шина тонкая и частота относительно низкая, поверхностный эффект будет незначительным.
Рассмотрим числовой пример. Медные шины высотой h = 2 см и толщиной 2a = 0,1 см имеют Y = 5,6 • 107 olg1 • lg1. | lg = 1. Потоки AC / -10 A, угловая частота = 105 рад / с. Вам необходимо определить, сколько раз плотность тока на краю шины превышает плотность тока, соответствующую равномерному распределению (если отсутствует поверхностный эффект).
Определить k = 1870 л / л, k = 1870.0.0005 = 0,935, 2La = 1,87. Является ли плотность тока на поверхности шины O = p, 2L th pa ih pl-sh2 ^ Q4- / sin2Z? Fl 3,167 -f- / 0,956 </ 16 * 25 ‘* ch2ka -J-cos2ka 3,32-0,292. 10 yh_d = 1870 K2 e’CH5 ° = 60,6 • 10 *. e / » 85 ‘a / mg. ~ 2.0.02.1.09. e’16’25’ b = — = = = 50,10 <a / m * равномерно распределенная плотность тока.
h-2a 0,02-0,001 Поэтому рассмотрим В среднем примере было обнаружено, что плотность тока на поверхности шины была только на 20% выше, чем однородная плотность тока 1.2).
Смотрите также:
| Глубина проникновения и длина волны. | Применение теоремы Умова — Пойнтинга для определения активного и внутреннего индуктивного сопротивления. |
| Магнитный поверхностный эффект. | Эффект близости. |

