Оглавление:




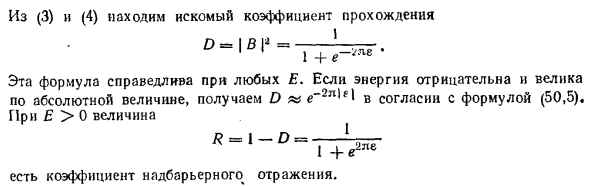

Прохождение через потенциальный барьер
- Преодоление потенциальных барьеров Учитывайте движение частиц в отображаемом типе поля Характеризуется возможностью ввода цифры 13 Барьер, -потенциальная энергия U (пк) Полная энергия E частицы превышена. В классической механике Потенциальный барьер Мы за частицы. В квантовом В механике частицы Вероятно, ненулевой «Пройди барьер» (о Это явление также упоминается как Про туннельный эффект) 1).
- Если Поле U (x) удовлетворяет условию Квазиклассические ямы, затем коэффициенты Коэффициент прохождения через барьер составляет Общая форма. Решите раньше, чтобы не прерывать дальнейшие вычисления Переведите следующие проблемы в переменную: Квазиклассическая волна Точка перегиба x = b (где U {x) Е Я L р / 1 1 г ^ я я 1 1 ^ но Рисунок 13 б Jr dr | 2 y 2 ta _ (s / 2-i) (S-2) ч x)
Эти условия, в частности: Барьер должен быть широким, поэтому фактор Отрывок в полуклассическом случае мал. Людмила Фирмаль
Пример такого типа уже обсуждался в вопросах 2 и 4 §25. § 50P R O X O Z D Y N I E CH E R E Z P O T E N C И A L N N Y B A R E R 227 U (x) 0, Напишите функцию (50.1) в следующем формате х f (x) = (x-V ‘4 e x p {i <2 м F »> 1/4 / В И сделайте круговую развязку справа налево с полукругом Верхняя полуплоскость: х x-b = regsr, i J l / x-bdx = sin ^ + r cos, б Кроме того, фаза <р изменяется от 0 до 7G. Во время функции байпаса Функция φ (x) сначала уменьшается, а затем увеличивается по абсолютной величине.
Равный концу раунда В φ (χ) = / (a m ^ V F ^ + f Следовательно, найдено следующее правило соответствия 1). _C ^ вице-президент Х х ^ e x p {i / p б х <б 1) При повороте справа налево через нижнюю полуплоскость функция f (x) сначала увеличивается, затем уменьшается по модулю и поворачивает налево Сохранить от полуоси (<p —Y —7r) до экспоненциально малых значений Экспоненциально большие функции (50.2) запрещены на «фоне».
В этом участке обхода φ (χ) растет экспоненциально из-за неточностей. Квазиклассическое приближение, экспоненциальное малое сложение потеряно, (P — »- 7G может расти в геометрической прогрессии Член, это было снова потеряно. 228 K V A ZI K L A S S I C H E S K I Y S L U W A H H. VII Подчеркните, что это правило означает определенный вид Классическая волновая функция времени (бежит к правой волне).
Разрешенная область, особенно следует использовать для миграции От последнего до районов, которые классически недоступны. Вернуться к расчету коэффициента передачи За пределами потенциальных барьеров. Падение частиц на барьер Из области I слева направо. Тогда я за барьером Только волны, которые проходят через барьер, распространяются и распространяются Направо.
Написать волновую функцию в этой области В форме F = j P dx + j б (50,3) Где v = p / m — скорость частицы, а D — плотность потока волны. Найти волновую функцию в области по правилу (50.2) Я внутри барьера: / D (1 ‘Φ = \ 71 EXP I T И VH о рйх jОXp d x-i J pd x). (50,4) Наконец, примените правило (47.5) и доберитесь до области I, прежде чем Барьеры: V- = 2, / -e x p- 6 а 1 J H <Jx) coS (i I Если эта функция введена В Д-е х р (- ^ / и дх (50,5)
Принять форму X = cos -2 (i f / VvVйJp d x + -) = 1 exp (i f pdx + 7 + j = v e * p (-U p d x ~ ′ i Первый член (уменьшается до плоской волны с осью X) φ ~ ewx / h ^ представляет волну, падающую на барьер, вторая Разрывная волна. Выбранная нормализация равна 1 Значение плотности магнитного потока падающей волны и, следовательно, значение D Плотность магнитного потока прошедшей волны соответствует желаемой Коэффициент, который проходит через барьер.
- Чтобы подчеркнуть это Формула может быть применена только тогда, когда показатель степени велик. Д м сама 1). Пока что поле U (x) Квазиклассические условия по всей длине барьера ( Только рядом с поворотным моментом Это). На самом деле, часто вам нужно бороться с неудачей Кривая потенциальной энергии с одной стороны Квазиклассическое приближение Применение будет.
Главный экспоненциальный фактор D остается Здесь то же самое, что и уравнение (50.5), но предыдущий показатель Новый элемент (равный единице (50,5)) изменен. Для него Необходимо рассчитать точную волну как принцип расчета Неквазиклассические функции соответствия Определяет внутреннюю квазиклассическую волновую функцию Барьеры. Z a z h 1.
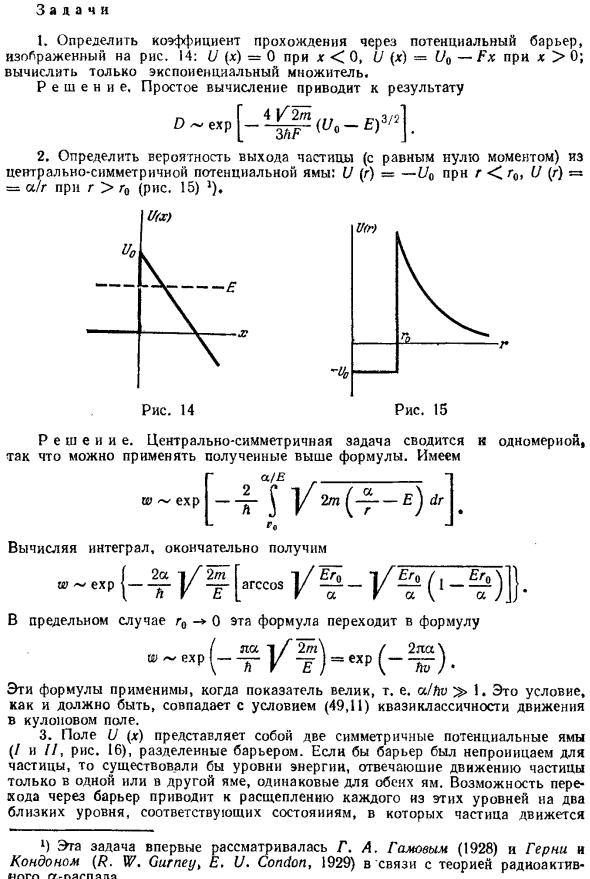
Определить коэффициент прохождения через потенциальные барьеры. 14: U (x) = 0, если x <0, U (x) = Uo-Fx, если x> 0. Людмила Фирмаль
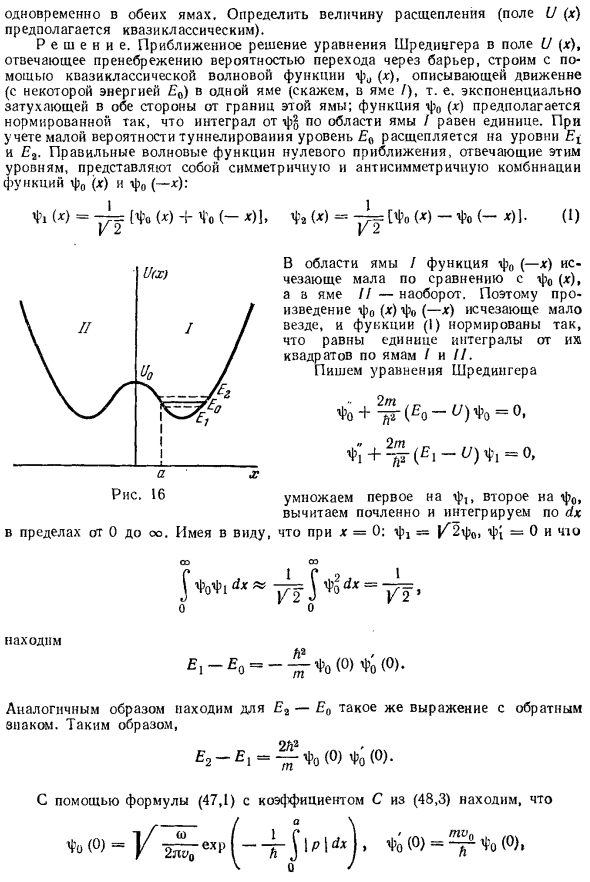
Вычислять только экспоненциальные коэффициенты. Результат получается простым расчетом -S) 3/2 СВЧ К. 2. Определяет вероятность появления частицы (нулевой момент) Из центросимметричной потенциальной ямы: U (r) = -Uo для r r> r (рис. 15) 2). Проблема симметрии центра решений сводится к одному измерению, Так что приведенная выше формула может быть применена.
У нас есть а / е 2P Перейти / ^ 2 м (~ E) др 1) Амплитуда равна Оказалось, что падающая и отраженная волны в Районе I были одинаковыми. Экспо Небольшие различия между ними в квазиклассическом приближении Будет потеряно. 2) Это проблема Г. Впервые рассмотрены Ф. Гамовым (1928) и Герни. Кондон (Р. У. Герни, Э. У. Кондон, 1929) в связи с теорией радиоактивности Collapse. 230 К В А ЗИ К Л А С С И С Х Е С К И Й С Л У Ш А Х Г Л. VII При вычислении интеграла, наконец, E g o _ / E go o L E go o L V (у)
В ограничительном случае go -Y 0 это выражение становится выражением ‘2 TGA \ ехр 7 га h = exp hv) Эти формулы применяются, когда показатель степени велик, т. Е. / Hv 1. Это условие Это должно быть, но согласуется с квазиклассическим условием (49.11) Движение подвесного поля. 3. Поле U (x) представляет две симметричные потенциальные ямы (7 и 77, рис. 16), разделенные барьером.
Когда барьер не может проникнуть Для частиц существует уровень Энергия, соответствующая движению частицы Только в той или иной яме В обе дырки. Возможность повторного Сплит через барьер Каждый из этих уровней близок к двум Уровень, соответствующий состоянию Частицы движутся одновременно В обеих ямах. Определить размер гонки Щепотка (поле U (x) является полу- Неклассическая).
Решение приближенное решение Уравнение Шредингера поля U (x), Игнорировать вероятность При прохождении через барьер он строится с использованием квазиклассической волновой функции Фаза (x), описывающая движение в одной скважине (включая энергию Eo) (Например, 7), т.е. экспоненциально затухают с обеих сторон гра Пространство этой ямы, так как предполагается, что функция φο (χ) нормализована, Святой Грааль из Пхо в области ямы 7 равен 1.
Подумайте о низкой вероятности Туннельный уровень Eo делится на уровень E1 и 7 ^ 2 Приближенные волновые функции нулевого порядка, соответствующие этим уровням Настроить симметричную и антисимметричную комбинацию функций fo (x) и fo (s): Рисунок 16 ФЛХ) = + Фо (-х)], ф2 (х) = -Фо (-х)]. В области скважины I функция φ (-x) очень мала по сравнению с φ0 (x) А я в яме — я наоборот.
Следовательно, произведение oo (x) oo (-x) очень мало Везде функция (1) нормирована, поэтому их интеграл Яма квадратная I I II. Напишите уравнение Шредингера ■ FP + ^ (Е0-и) ф0 = 0, час φ, u ^ (E2 m, 1-u) φ1 = 0, Умножим первое на φ1, умножим второе на φ0, вычтем слагаемые по слагаемым и интегрируем По dx в диапазоне от 0 до sy. χ = 0, φ = / / 2φο, φ [= 0 Joo ooF0Ф1dx «~ ^ = Jф1dx = — ^ = И oV2 J Guy y / 2 ‘ узнать Е1-Е0 = -фо (0) ф’о (0).
T Аналогично, для E 2-Eo противоположная формула находит ту же формулу Знакомый. Вот так 2 /? 2 E2-E 1 = -фо (0) ph’o (0). T Используя коэффициент C в уравнениях (47.1) и (48.3), / —— Fo (0) = J ^^ exp («^ / lpld: r)’ ^ o (0) = 1 ^ фо (0), о Где vo = l / 2 (Uo-Eo) / t, как это E 2-Ex = -exp J \ p \ dx -a (A — это точка поворота, соответствующая энергии Eo, см. Рисунок 16). 4. Определить точное значение коэффициента передачи D (не заранее) (Предполагая небольшой) параболический потенциальный барьер U (x) = = —Kx 2/2 (Е.С. Кете, 1 9 35) х).
Для значений решения k и E движение является квазиклассическим Достаточно долго \ х \, где \ т 1 х Асимптотическая форма решения уравнения Шредингера φ = постоянный £ ± g £ -1 / 2 exp (± g £ 2/2), 1) Решение этой проблемы также может быть применено для доступа Точная близость к вершине барьера U (x) в зависимости от квадратичной функции От х около максимума. 232 K V A ZI K L A S S I C H E S K I Y S L U W A H H.
VII Где введено обозначение: £ = X (H * V / 4e = e.I ™ \ ч 2) от Y до футов Я заинтересован в решении, где х + оо включает только прошлое Волна, распространяющаяся через барьер, то есть волна, распространяющаяся слева направо. Put φ = В £ г £ _ _1 / 2 exp (r 2 2/2) при x-> сю, (1) Φ = (-)) — r e-1/2 exp (-r 2 2/2) + ((-)) r __1 // 2 exp (r 2 2/2) как x- °∞ (2) Первый член в (2) падает, а второй член отражается Волна (направление распространения волны Эта фаза).
Отношения между A и B могут быть найдены на основе следующих фактов: Все асимптотические формулы φ хорошо разделены Плоская площадь комплексной переменной £. Следите за изменениями Функция (1) При движении вверх по полукругу с большим радиусом p Его полуплоскость £: £ = pe *, r £ 2 = p2 (-sin 2 ^ + r cos2φ), И <р варьируется от 0 до 7G.
Функция (1) заканчивается в результате обхода Используя коэффициент во втором члене (2) A = B (e «) ~ 1/2 = -rB e ~ L £; (3) Сечение пути (π / 2 <(p <τm), где модуль | exp (r £ 2/2) | экспоненциально Если оно большое, экспоненциально малая сумма теряется. (2) Дайте первый член х).
При нормализации падающей волны, выбранной в (2), условия хранения Количество частиц составляет И | 2 + | B | 2 = 1 (4) Найти нужный коэффициент передачи из (3) и (4) D = \ B \ 2 = 1 / (1 + e ~ 2x £). Это выражение действительно для всех E. Энергия отрицательна, Абсолютный размер, получи D ~ e-27Г1 £ 1 по форме Рой (50,5). Значение, если E> 0 R = l-D = 1 / (1 + е2же) Коэффициент отражения барьера.
Смотрите также:
| Правило квантования Бора-Зоммерфельда | Вычисление квазиклассических матричных элементов |
| Квазиклассическое движение в центрально-симметричном поле | Вероятность перехода в квазиклассическом случае |
Если вам потребуется заказать решение по физике вы всегда можете написать мне в whatsapp.

