Оглавление:









Прогрессивные волны
Вместе с потенциалом скорости гидромеханики или это движение представляет собой стоячую волну, которая отличается от предыдущей. Во-первых, есть узел в том месте, где была волна живота, и наоборот. Во-вторых, когда частица предыдущего движения находится в крайнем положении, частица будет находиться в равновесии с текущим движением, и наоборот, потому что фаза колебания текущего движения и предыдущего движения отличается от минуте цикла.
Далее мы суммируем возможности обоих. Поскольку сумма решений системы из-за линейности этих уравнений также является решением системы, эта возможность определяет невращательное волновое движение. И снова стоячие волны задают тот же вопрос.
- Каков внешний вид свободных поверхностей, скорость и траектория движения отдельных частиц?
- Тип свободной поверхности определяется по формуле: если ввести обозначение еще раз, то уравнение переписывается следующим образом. Профиль волны получается в виде косинусной волны, а амплитуда волны снова находится на длине волны.
Однако принципиальное отличие этой волны от стоячей заключается в том, что форма свободной поверхности движется в определенном направлении без изменения формы. Людмила Фирмаль
На самом деле свая и дно профиля волны расположены в своих точках. То есть в разные моменты, в разное время.
Вы можете видеть, что все пики волн и вся волна смешиваются со скоростями в направлении отрицательной оси. С тех пор для скорости распространения волны, можно использовать следующую формулу. Опять же заметим, что движется только форма свободной поверхности, а сами частицы жидкости совершают лишь небольшие колебания вблизи положения равновесия.
- Скорость движения отдельных частиц определяется по формуле Упрощенные уравнения легче найти, построив функции потока. Возможности соответствуют текущему функционалу.
- Таким образом, текущая функция желаемого. Итак, уравнение линии потока имеет вид.
Поэтому обтекаемая линия имеет ту же форму, что и в случае стоячих волн. Однако из-за времени в уравнении обтекания обтекание не является стационарным. Поэтому траектории движения частиц жидкости не совпадают с траекториями движения частиц жидкости.
To выведя приближенную траекторию движения этих частиц, мы поступим так, как описано выше, то есть с помощью формулы, устанавливающей эти переменные равными значению, которое они имеют для положения равновесия. Людмила Фирмаль
Когда вы интегрируете эти уравнения прогрессивных волн к установившемуся движению , это выглядит так. Чтобы исключить время получения уравнения орбиты частицы, приближенная траектория движения жидкой частицы равна радиусу, тем меньшему, чем глубже окружность, в которой находится рассматриваемая частица.
Для поверхностных жидких частиц этот радиус равен амплитуде. При глубине, равной длине волны, этот радиус в несколько раз меньше. Каждая частица представляет собой круг по часовой стрелке и наоборот. Дело в том, что если обозначить углы, составляющие радиус-вектор с отрицательной осью через и соединить центр окружности точкой, то очевидно.
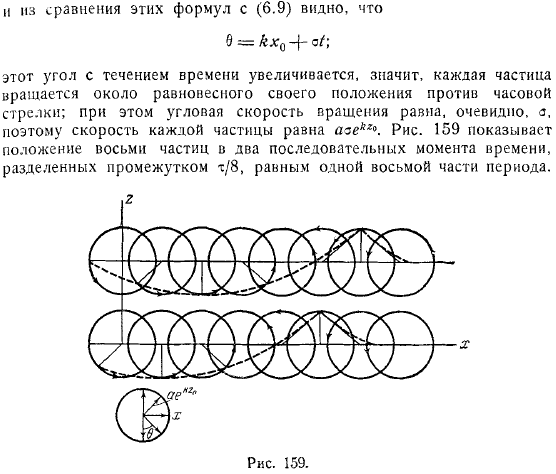
Из сравнения этих выражений получается. Этот угол увеличивается с. Другими словами, каждая частица вращается против часовой стрелки вокруг своего положения равновесия. Между тем, угловая скорость вращения очевидна. Таким образом, скорости каждой частицы будут равны.
Показано расположение частиц в последовательных точках, разделенных промежутком, равным минуте периода. За определенный промежуток времени профиль волны переместился на минут на левую длину волны, не меняя своего внешнего вида, то есть профиль волны перемещается влево вместе со скоростью. Кроме того, частицы в верхней части волны четко проходят верхнюю часть своей траектории, поэтому они движутся влево.
То есть она движется в том же месте, где распространяется волна (конечно, с меньшей скоростью). В депрессии направление движения частиц противоположно направлению распространения волны . Также рассчитайте давление по формуле.
Потому что разница бесконечно мала. Если вы замените его на первый член справа, вы увидите следующее: это означает, что частицы, находящиеся в одной горизонтальной плоскости в состоянии равновесия, каждый раз, когда они движутся, давление остается постоянным, и кроме того, они образуют ту же поверхность, что и равновесное состояние. Частицы свободной поверхности жидкости отличаются только своими частицами от остальных.
Из этого можно сделать вывод, что за свободную поверхность жидкости можно принять поверхность, образованную частицами, что одно и то же. Таким образом, можно удалить слой жидкости, не нарушая волну оставшейся жидкости. Поэтому каждый слой жидкости колеблется независимо от каждого.
При необходимости можно заменить снятый слой жидкости таким же слоем другой жидкости разной плотности. Вы можете рассматривать потенциальную скорость движения точно так же, как и в предыдущем методе. Профиль волны для него представляет собой косинус, который движется в направлении положительной оси с той же скоростью.
Траектория движения частиц снова становится кругом того же радиуса, только эти круги выполняются по часовой стрелке. Он обеспечивает пластину, которая показывает, как скорость распространения бегущей волны и ее период изменяется в зависимости от. Этот случай, он очень глубок по сравнению с этой длиной волны жидкости .

