Оглавление:
Прогнозирование с использованием показателей средних характеристик ряда динамики
Одним из наиболее распространенных методов краткосрочного прогнозирования социально-экономических явлений и процессов является экстраполяция, т. е. распространение прошлых и настоящих закономерностей, связей, соотношений на будущее. Наиболее простым методом экстраполяции одномерных рядов динамики является использование средних характеристик: среднего уровня, среднего абсолютного прироста и среднего темпа роста.
При использовании среднего уровня ряда динамики в прогнозировании социально-экономических явлений прогнозируемый уровень принимается равным среднему значению уровней ряда в прошлом:

Прогноз вычисляется на 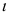 моментов времени вперед (период упреждения), т. е. до момента
моментов времени вперед (период упреждения), т. е. до момента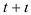 (горизонт прогнозирования). Получается прогностическая точечная оценка, которая, вообще говоря, не совпадает с фактическими данными. Поэтому для средней указывается доверительный интервал прогноза
(горизонт прогнозирования). Получается прогностическая точечная оценка, которая, вообще говоря, не совпадает с фактическими данными. Поэтому для средней указывается доверительный интервал прогноза
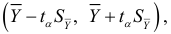
где 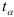 табличное значение
табличное значение 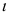 -критерия Стьюдента с
-критерия Стьюдента с 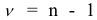 степенями свободы и уровнем доверия
степенями свободы и уровнем доверия 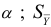 — средняя квадратичная ошибка средней:
— средняя квадратичная ошибка средней:
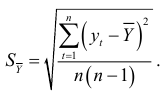
Применение доверительного интервала для прогнозирования увеличивает степень надежности прогноза, но, тем не менее, прогнозируемый показатель равен среднему уровню. Чтобы учесть вариацию показателя вокруг средней в прошлом и будущем, для прогностической величины вычисляют доверительный интервал:
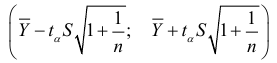
так как общая дисперсия, связанная с колебаемостью выборочной средней и варьированием уровней ряда вокруг средней, будет равна 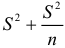 , где
, где
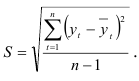
Если общая тенденция развития динамического ряда является линейной или выполняется неравенство:
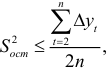
где 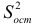 — остаточная дисперсия, не объясненная экстраполяцией по среднему абсолютному приросту;
— остаточная дисперсия, не объясненная экстраполяцией по среднему абсолютному приросту; 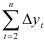 — общий прирост показателя от начального уровня до конечного, то выполняется экстраполяция по среднему абсолютному приросту. Прогнозное значение уровня
— общий прирост показателя от начального уровня до конечного, то выполняется экстраполяция по среднему абсолютному приросту. Прогнозное значение уровня 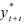 определяют по формуле:
определяют по формуле:
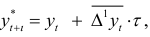
где 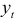 — уровень ряда динамики, принятый за базу экстраполяции;
— уровень ряда динамики, принятый за базу экстраполяции; 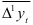 -средний абсолютный прирост;
-средний абсолютный прирост; 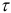 — период упреждения.
— период упреждения.
Если развитие ряда динамики списывается геометрической прогрессией или показательной кривой, то экстраполяция выполняется по среднему темпу роста. Прогнозируемый уровень ряда определяется по следующей формуле:
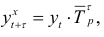
где 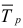 — средний темп роста;
— средний темп роста; 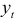 — уровень ряда динамики, принятый за базу экстраполяции.
— уровень ряда динамики, принятый за базу экстраполяции.
В качестве базового уровня для экстраполяции берется последний уровень ряда уп, так как будущее развитие начинается именно с этого уровня. В некоторых случаях в качестве базового уровня лучше брать расчетный уровень, соответствующий тренду, описывающему динамический ряд. Для этого определяют экспоненциальную кривую и на ее основе находят базовый уровень. Для выбора базового уровня можно прибегнуть к усреднению нескольких последних уровней, т. е. вычислить экспоненциальную или геометрическую среднюю нескольких последних уровней.
Отметим, что если уровни ряда динамики непрерывно возрастают за рассматриваемый период, то средний темп роста вычисляют по формуле
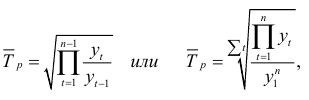
где 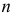 — число цепных темпов роста;
— число цепных темпов роста; 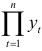 — произведение уровней динамического ряда;
— произведение уровней динамического ряда; 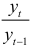 — цепной темп роста;
— цепной темп роста; 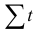 — сумма порядковых номеров уровней динамического ряда; ух — начальный уровень ряда.
— сумма порядковых номеров уровней динамического ряда; ух — начальный уровень ряда.
Если же уровни ряда динамики в одни годы растут, а в другие снижаются, то для вычисления среднего темпа роста можно воспользоваться следующей формулой:
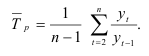
Доверительный интервал прогноза по среднему темпу роста может быть построен в случае, когда средний темп роста определяется по экспоненциальной функции.
Указанные способы экстраполяции тренда динамического ряда являются весьма приближенными.
Пример 9.1.
Выпуск цемента за период с 1975 по 1990 г. характеризуется динамическим рядом, представленным в табл. 9.1.
Проиллюстрируем построение прогнозов с использованием средних характеристик данного ряда динамики: среднего уровня, среднего абсолютного прироста и среднего темпа роста.
При экстраполяции на основе среднего уровня ряда используется принцип, при котором прогнозируемый уровень принимается равным среднему значению уровней в прошлом:
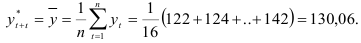

Доверительный интервал прогноза для средней вычислим по формуле (9.1):
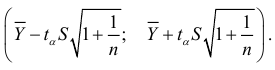
Табличное значение 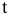 -статистики Стьюдента
-статистики Стьюдента 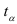 с
с 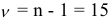 степенями свободы при уровне доверия
степенями свободы при уровне доверия 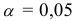 равно
равно 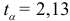 . Среднее квадратичное отклонение, связанное с выборочной средней и варьированием уровней ряда вокруг средней,равно:
. Среднее квадратичное отклонение, связанное с выборочной средней и варьированием уровней ряда вокруг средней,равно:
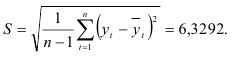
Подставив найденные значения в формулу (9.1), получим доверительный интервал (116,1639; 143,9561), который с доверительной вероятностью 0,95 включает прогнозируемое значение производства цемента равно: 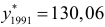 млн.т.
млн.т.
Считая, что общая тенденция производства цемента является линейной, прогноз производства цемента на 1991г. вычислим по среднему абсолютному приросту: 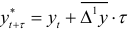 . За базу экстраполяции примем среднее арифметическое трех последних уровней исходного динамического ряда:
. За базу экстраполяции примем среднее арифметическое трех последних уровней исходного динамического ряда:
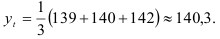
Средний абсолютный прирост
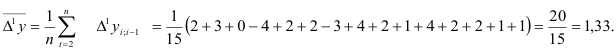
Тогда прогнозное значение уровня на 1991г.
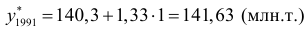
Экстраполяция по среднему темпу роста осуществляется по формуле
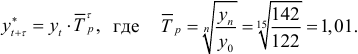
За базу экстраполяции примем среднее арифметическое трех последних уровней, т. е. 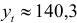 . В этом случае прогнозируемый уровень ряда равен:
. В этом случае прогнозируемый уровень ряда равен:
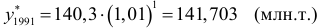
Доверительные интервалы прогноза по среднему абсолютному приросту и среднему темпу роста могут быть получены в том случае, когда общая тенденция развития является линейной или когда средний темп роста определяется с помощью статистического оценивания параметров экспоненциальной кривой.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

