Оглавление:
Прогнозирование с использованием авторегрессионных моделей
В основе метода прогнозирования с использованием авторегрессионых моделей лежит гипотеза о стационарности изучаемого явления, т.е. о сохранении статистических характеристик явления без изменения на ретроспективном промежутке времени, в настоящем и будущем.
При прогнозировании важен выбор модели авторегрессии наименьшего порядка с целью обеспечения требуемой точности описания данных.
При использовании модели авторегрессии порядка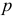 
нужно проверить существенность автокорреляции остатков в этой модели, применив критерий Дарбина-Уотсона. Затем проверяется условие нормальности распределения случайной компоненты 
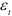путем исследования показателей асимметрии 
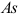и эксцесса 
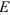, а также их средних квадратичных ошибок 
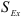и 
.
И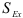так, прежде чем использовать при прогнозировании авторегрессионую моделью, нужно убедиться в следующем.
- Случайная компонента динамического ряда представляет собой стационарности в широком смысле случайный процесс. Для определения ее стационарности находят значения автокорреляционной функции для случайной компоненты, используя
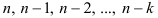уровней динамического ряда. В результате получают 
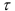групп коэффициентов автокорреляции, в каждую из которых будет входить 
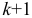коэффициентов. Затем, используя 
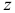— критерий Фишера, устанавливают однородность коэффициентов автокорреляции, входящих в одну и ту же группу. Если гипотеза об однородности не отвергается для всех групп, можно сделать вывод о том, что отклонения 
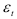представляют собой стационарный в широком смысле случайный процесс. - Случайная компонента 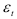является случайной величиной, не зависящей от времени.
- Отклонения от расчетных значений, полученных по авторегрессионой модели, являются выборкой нормально распределенной случайной величины с математическим ожиданием, равным нулю.
- Отклонения от расчетных значений, полученных по авторегрессионой модели, не содержат автокорреляции.
Если при проверке установлено, что для динамического ряда не выполняется хотя бы одно из перечисленных выше условий, то авторегрессионая модель не применяется для описания исследуемого динамического ряда.
Установив выполнимость указанных условий, вычисляют коэффициенты авторегрессионой модели и определяют, насколько точно можно оценить эти коэффициенты по имеющейся выборке. Оценки коэффициентов авторегрессии
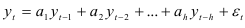
являются случайными величины со средними, равными, и дисперсиями, вычисляемыми по формулам
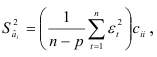
где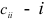 
-и диагональный элемент матрицы, обратной матрице системы нормальных уравнений для определения коэффициентов 
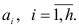. Величина 
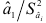имеет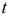 
-распределение Стьюдента с 
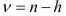степенями свободы. После вычисления коэффициентов авторегрессионой модели прогнозируют значения 
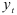, на период 
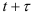по авторегрессионой модели следующим образом.
Сначала вычисляют значение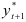 
по формуле
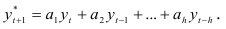
Вычисленное значение 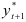подставляют в модель
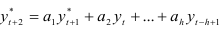
и находят значение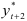 
и т.д.
Важную роль играет оценка погрешности прогноза, полученного с помощью авторегрессионой модели. Для построения доверительного интервала прогноза используется тот факт, что остатки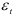 
в уравнении авторегрессии распределены нормально с нулевым математическим ожиданием и дисперсией 
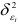. Если коэффициенты авторегрессионой модели известны из других выборок или из априорных соображений, то оценка дисперсии случайной величины 
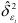вычисляется по формуле
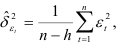
где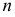 
— число уровней динамического ряда; 
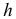— порядок авторегрессионой модели.
Случайная величина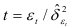 
имеет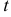 
— распределение Стьюдента 
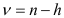степенями свободы. Тогда вероятность того, что величина 
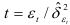не превосходит, можно определить по формуле 
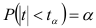, откуда следует, что
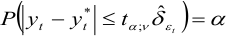
или
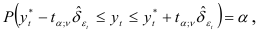
где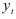 
— истинное значение исследуемого параметра, 
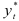— предсказанное значение.
Если же коэффициенты авторегрессионой модели вычислены на основании исследуемого динамического ряда, то оценка дисперсии остатков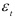 
вычисляется по формуле
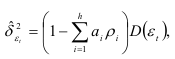
где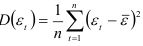 
— дисперсия динамического ряда 
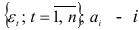-й коэффициент авторегрессии; 
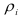— коэффициент автокорреляции 
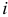-го порядка.
Доверительный интервал прогноза будет аналогичным:
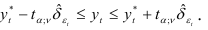
Пример 9.8.
Рассмотрим динамический ряд, характеризующий объем производства фирмы «Эврика» (табл.9.10).
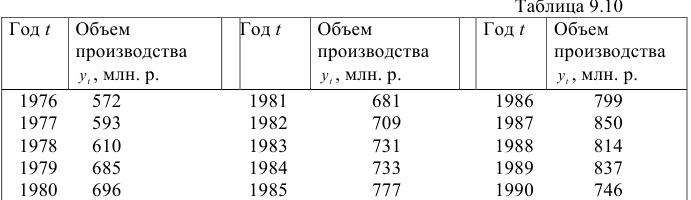
Для описания тренда данного ряда динамики выберем линейную функцию
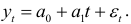
Решив систему нормальных уравнений
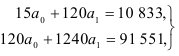
получим:
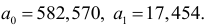
Тогда уравнение тренда будет иметь вид:
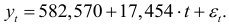
Проверим выполнимость предпосылок возможности использования авторегрессионых моделей для прогнозирования.
Прежде всего проверим гипотезу о случайном характере отклонений от тренда с помощью критерия серий:
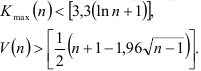
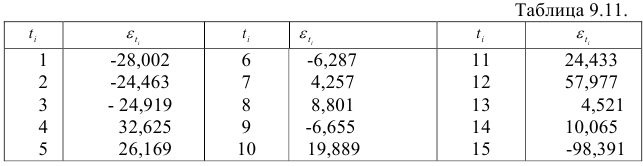
Построив вариационный ряд -98,391; -28,002; -24,919; -24,463; -6,655; -6,287; 4,257; 4,521; 8,801; 10,065; 19,889; 24,433; 26,169; 32,625; 57,977, определим медиану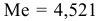 
и образуем последовательность из плюсов и минусов по следующему правилу. На 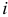-м месте ставим плюс, если 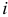-й уровень динамического ряда остатков превосходит медиану, и минус, если он меньше медианы. Получим последовательность знаков:
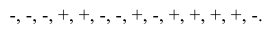
Отсюда найдем протяженность самой длинной серии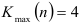 
и общее число серий 
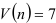. Тогда из неравенств
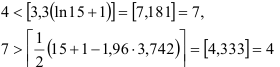
следует, что отклонения от тренда носят случайный характер.
Далее проверяем гипотезу о том, что случайная компонента представляет собой стационарный случайный процесс. Для этого находим значения автокорреляционной функции соответственно для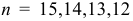 
уровней динамического ряда, т.е. из расчетов последовательно исключаются первый, второй, третий и четвертый уровни. Большее число уровней исключать нецелесообразно, так как ряд отклонений слишком короток. Для всех значений коэффициентов автокорреляции вычислены значения 
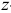-критерия Фишера:
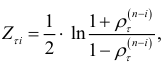
средние для каждой группы
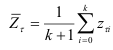
и величина
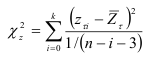
для каждого сдвига 
. Результаты расчетов приведены в табл.9.12.
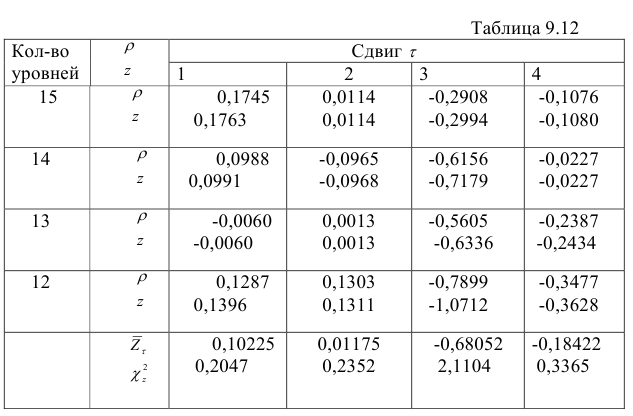
Вычисленные значения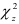 
представленные в последней строке табл.9.12, сравниваем с квантилем 
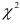-распределения для уровня значимости 
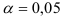и числа степеней свободы 
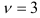, т.е. с 
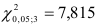. Из таблицы видим, что фактические значения 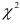меньше . Следовательно, гипотеза об однородности коэффициентов автокорреляции для каждого сдвига не отвергаются и отклонения от линейного тренда являются стационарным в широком смысле случайным процессом.
Для выбора порядка авторегрессионой модели рассмотрим значения автокорреляцио ной функции, представленные в табл.9.13, и построим коррелограмму (рис.9.2).
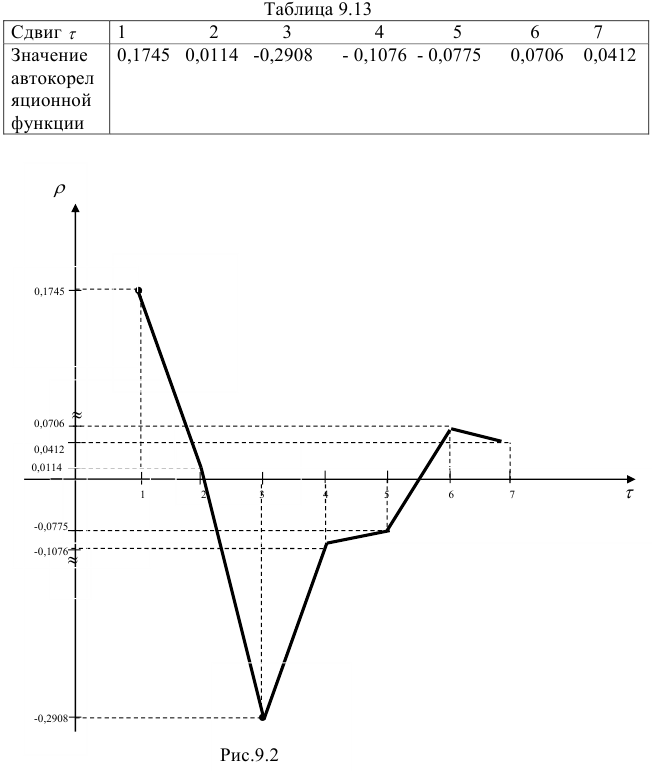
На рис. 9.2 видно, что, начиная с третьего сдвига, происходит затухание коррелограммы, т.е. связь с прошлым ослабевает. Это свидетельствует о том, что нужно строить авторегрессионые модели не выше третьего порядка. Так как для отклонений от линейного тренда автокорреляционная функция достигает наибольшего значения на первом сдвиге, то строим три модели соответственно 1-го, 2-го и 3-го порядков:
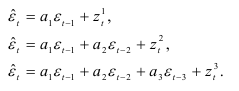
Единственный коэффициент модели первого порядка равен коэффициенту автокорреляции первого порядка:
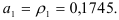
Коэффициенты авторегрессионой модели второго порядка находим из соотношений:
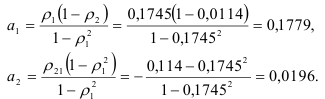
Используя коэффициенты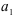 
и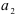 
модели авторегрессии второго порядка и коэффициенты автокорреляции 
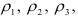находим коэффициенты модели третьего порядка:
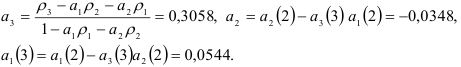
Применим критерий Бартлетта для определения порядка авторегрессионой модели. Для этого вычислим сумму квадратов остатков для моделей:
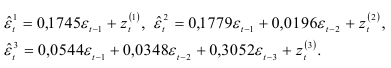
Значения критерия Бартлетта для сравнения моделей первого и второго, первого и третьего, второго и третьего порядков соответственно равны:
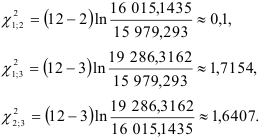
Табличные значения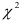 
. Для уровня значимости
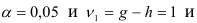
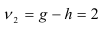
степени свободы равны:
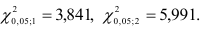
Следовательно, гипотеза о том, что авторегрессионые модели второго и третьего порядков дадут лучшие результаты, отвергается, т.е. для прогнозирования можно применять авторегрессионую модель первого порядка. Этот вывод подтверждается и сравнением финальных ошибок прогноза на текущий момент времени:
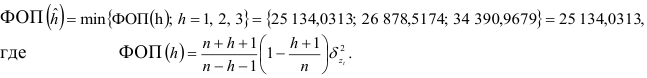
Для выбранной авторегрессионой модели первого порядка проверим существенность автокорреляции остатков, пользуясь критерием Дабрина-Уотсона. Для рассматриваемого примера
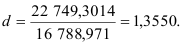
Так как при уровне значимости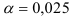 
выполняется неравенство
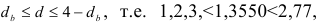
то с вероятностью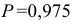 
можно утверждать, что автокорреляция в отклонениях от авторегрессионой модели первого порядка отсутствует.
Проверим условие нормальности распределения величины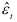 
, используя показатели асимметрии и эксцесса:
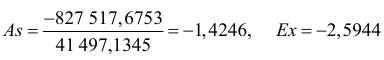
и средние квадратичные ошибки коэффициентов асимметрии и эксцесса:
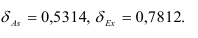
Из значений асимметрии и эксцесса и их ошибок следует, что неравенства
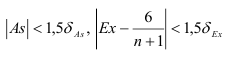
не выполняются, т.е. отклонения от авторегрессионой модели первого порядка не подчиняются нормальному закону распределения.
Учитывая результаты проверок основных предпосылок, делаем вывод о том, что отклонения от линейного тренда могут быть аппроксимированы авторегрессионой моделью
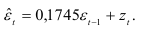
Из уравнения тренда (9.18) выразим случайную компоненту
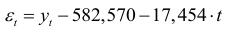
и подставим это значение в авторегрессионую модель (9.19) первого порядка:
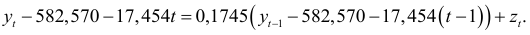
в результате преобразований получим следующую модель прогноза объема производства фирмы «Эврика»:
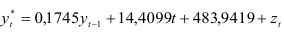
Прогноз объема производства на 1991 г. по этой модели
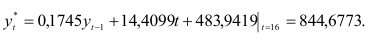
Доверительный интервал прогноза построить нельзя, так как вероятностные оценки прогноза предполагают нормальное распределение случайной величины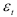 
что для рассматриваемого примера не подтверждается.
Проверка условий 1—4, приведенных в начале параграфа, для данного примера показал, что не выполняется условие 3. Это означает, что рассматриваемый процесс может описываться авторегрессией более высокого порядка. Такой вывод можно сделать, и рассматривая табл. 9.13 значений автокорреляционной функции.
Таким образом, оценка порядка авторегрессионой модели являются очень «тонким» вопросом. Определяя порядок авторегрессионой модели, нужно учитывать внутреннюю структуру экономических процессов за прошлые периоды времени. Небольшое число уровней динамического ряда также сказывается при выборе порядка авторегрессионой модели.
Некоторую помощь в решении этого вопроса может оказать исследование конкретных процессов авторегрессии, которым соответствуют авторегрессионые модели различного порядка. Тогда возможный порядок авторегрессии можно оценить путем сопоставления с некоторыми стандартными моделями.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:
