Оглавление:
Прогнозирование методом гармонических весов
Автор метода гармонических весов польский статистик 3. Хевиг предложил проводить экстраполяцию по скользящему тренду. При этом отдельные точки ломаной линии взвешиваются с помощью гармонических весов, что позволяет более поздним уровням динамического ряда придавать больший вес.
Рассмотрим временной ряд 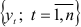 , математическая модель которого имеет вид
, математическая модель которого имеет вид 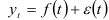 ,
,
где 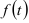 — неслучайная функция времени (тренд);
— неслучайная функция времени (тренд); 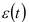 — стационарная случайная компонента.
— стационарная случайная компонента.
Если нет достаточно достоверной априорной информации о закономерностях изменения изучаемого экономического явления, то простая экстраполяция по тренду может привести к существенным ошибкам. Поэтому условно можно предположить, что некоторым приближением фактического тренда 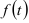 — является ломаная линия, каждое звено которой сглаживает заданное число уровней динамического ряда
— является ломаная линия, каждое звено которой сглаживает заданное число уровней динамического ряда 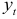 . Таким образом, ломаную линию можно представить как скользящий тренд. Проводя экстраполяцию по скользящему тренду и взвешивая при этом отдельные точки ломаной линии, с тем чтобы более поздним наблюдениям придать больший вес, получаем прогноз. Доверительный интервал для прогнозируемых показателей строится с использованием неравенства Чебышева.
. Таким образом, ломаную линию можно представить как скользящий тренд. Проводя экстраполяцию по скользящему тренду и взвешивая при этом отдельные точки ломаной линии, с тем чтобы более поздним наблюдениям придать больший вес, получаем прогноз. Доверительный интервал для прогнозируемых показателей строится с использованием неравенства Чебышева.
Для применения метода гармонических весов ряд динамики разбивается на интервалы, каждый из которых содержит 3-5 уровней. Число интервалов 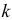 меньше
меньше 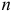 . Для каждого интервала определяется линейный тренд
. Для каждого интервала определяется линейный тренд
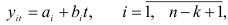
Причем для

для
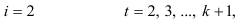
для
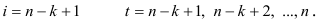
Оценивание параметров скользящего тренда осуществляется методом наименьших квадратов. Вычислив оценки параметров 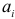 и
и 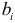 , получим
, получим 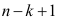 уравнение. Вычислим далее значение
уравнение. Вычислим далее значение 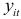 в точках
в точках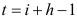 , где
, где 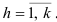 . Для каждого уравнения
. Для каждого уравнения 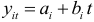 получим число значений функции
получим число значений функции 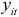 , равное числу уровней, содержащихся в интервале скольжения. Образуем множества
, равное числу уровней, содержащихся в интервале скольжения. Образуем множества 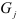 значений функции —
значений функции — 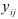 для которых
для которых 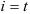 . Эти функции обозначим
. Эти функции обозначим 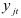 , а число таких функций —
, а число таких функций — 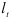 . Вычислим средние функций, содержащихся в построенных множествах:
. Вычислим средние функций, содержащихся в построенных множествах:
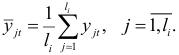
Соединив точки 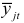 отрезками прямой, получим тренд исследуемого динамического ряда в виде ломаной линии.
отрезками прямой, получим тренд исследуемого динамического ряда в виде ломаной линии.
Затем проверим гипотезу о том, что отклонения 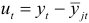 от скользящего тренда имеют случайный характер. Для проверки гипотезы
от скользящего тренда имеют случайный характер. Для проверки гипотезы 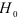 , состоящий в том, что отклонения от скользящего тренда образуют стационарный процесс, строится автокорреляционная функция, которая представляет собой множество коэффициентов корреляции между динамическим рядом, состоящим из отклонений
, состоящий в том, что отклонения от скользящего тренда образуют стационарный процесс, строится автокорреляционная функция, которая представляет собой множество коэффициентов корреляции между динамическим рядом, состоящим из отклонений 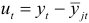 , и этим же рядом, сдвинутым относительно первоначального положения на
, и этим же рядом, сдвинутым относительно первоначального положения на 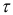 моментов времени. Нормированная автокорреляционная функция отклонений вычисляется по формуле
моментов времени. Нормированная автокорреляционная функция отклонений вычисляется по формуле
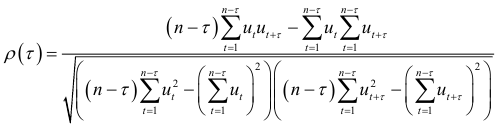
где
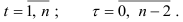
Величину 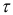 называют сдвигом. Сдвиг, которому соответствует наибольший коэффициент автокорреляции, называют временным лагом. График нормированной автокорреляционной функции назы вают коррелограммой.
называют сдвигом. Сдвиг, которому соответствует наибольший коэффициент автокорреляции, называют временным лагом. График нормированной автокорреляционной функции назы вают коррелограммой.
Для построения коррелограммы на оси абсцисс откладывают значения 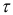 , а на оси ординат — значения коэффициентов автокорреляции
, а на оси ординат — значения коэффициентов автокорреляции 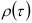 . Затем точки с координатами
. Затем точки с координатами 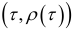 соединяют отрезками прямой. В результате получают ломаную линию, которая и называется коррелограммой.
соединяют отрезками прямой. В результате получают ломаную линию, которая и называется коррелограммой.
При вычислении коэффициентов автокорреляции с ростом 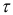 число коррелируемых пар уменьшается, а известно, что при небольшом числе наблюдений существенными оказываются лишь большие коэффициенты. Поэтому наибольшее значение
число коррелируемых пар уменьшается, а известно, что при небольшом числе наблюдений существенными оказываются лишь большие коэффициенты. Поэтому наибольшее значение 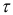 должно быть таким, чтобы число пар наблюдений оказалось достаточным для вычисления коэффициентов автокорреляции
должно быть таким, чтобы число пар наблюдений оказалось достаточным для вычисления коэффициентов автокорреляции 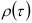 . На практике ориентируются на правило, из которого следует, что
. На практике ориентируются на правило, из которого следует, что 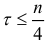 .
.
Значения автокорреляционной функции образуют ряд
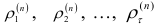
(верхний индекс означает число наблюдений, для которого вычисляется автокорреляционная функция). Затем исключают из динамического ряда первый или последний уровень и вычисляют значения автокорреляционной функции
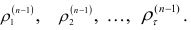
Продолжая указанный процесс, исключают 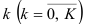 уровней динамического ряда и вычисляют значения
уровней динамического ряда и вычисляют значения 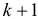 автокорреляционных функций. Таким образом, получают
автокорреляционных функций. Таким образом, получают 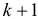 групп коэффициентов автокорреляции, в каждой из которых будет
групп коэффициентов автокорреляции, в каждой из которых будет 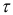 коэффициентов. Отклонения от скользящего тренда образуют стационарный в широком смысле процесс, если коэффициенты автокорреляции, входящие в одну и ту же группу, однородны. Проверка на однородность коэффициентов автокорреляции производится следующим образом. Для каждого
коэффициентов. Отклонения от скользящего тренда образуют стационарный в широком смысле процесс, если коэффициенты автокорреляции, входящие в одну и ту же группу, однородны. Проверка на однородность коэффициентов автокорреляции производится следующим образом. Для каждого 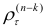 входящего в
входящего в 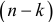 — ю группу, вычисляют
— ю группу, вычисляют 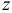 критерий:
критерий:
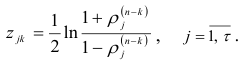
Затем для этой группы находят среднюю
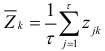
и вычисляют величину
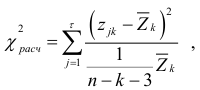
которая распределена по закону хи- квадрат с 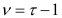 степенями свободы.
степенями свободы.
Тогда, сравнивая вычисленное значение величины (9.13) с табличным, при 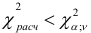 с вероятностью
с вероятностью 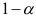 принимаем гипотезу об однородности рассматриваемой группы коэффициентов автокорреляции. Аналогичную проверку однородности проводим для всех групп коэффициентов автокорреляции. Если гипотеза об однородности принимается для всех групп, то делаем вывод о том, что отклонения от скользящего тренда образуют стационарный в широком смысле случайный процесс. Кроме того, если значения автокорреляционной функции, вычисленные для ряда отклонений от скользящего тренда, уменьшаются, это значит, что более поздняя информация сильнее отражается на прогнозируемой величине, чем более ранняя.
принимаем гипотезу об однородности рассматриваемой группы коэффициентов автокорреляции. Аналогичную проверку однородности проводим для всех групп коэффициентов автокорреляции. Если гипотеза об однородности принимается для всех групп, то делаем вывод о том, что отклонения от скользящего тренда образуют стационарный в широком смысле случайный процесс. Кроме того, если значения автокорреляционной функции, вычисленные для ряда отклонений от скользящего тренда, уменьшаются, это значит, что более поздняя информация сильнее отражается на прогнозируемой величине, чем более ранняя.
Установив, что отклонения образуют стационарный процесс, вычисляем приросты, равные разностям средних значений скользящих трендов:
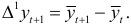
Средняя приростов вычисляется по формуле
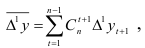
где 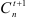 гармонические коэффициенты, удовлетворяющие следующим условиям:
гармонические коэффициенты, удовлетворяющие следующим условиям:
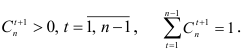
Гармонические коэффициенты 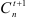 определяем так, чтобы более поздним наблюдениям придавались большие веса. Для этого полагаем
определяем так, чтобы более поздним наблюдениям придавались большие веса. Для этого полагаем
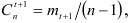
где
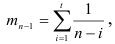
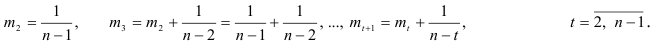
Следовательно,
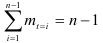
и гармонические коэффициенты 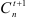 удовлетворяют условиям (9.14).
удовлетворяют условиям (9.14).
Предположим, что приросты 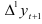 являются значениями случайной величины
являются значениями случайной величины 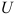 с математическим ожиданием
с математическим ожиданием 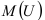 и дисперсией
и дисперсией 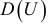 . Тогда их оценками будут средняя приростов
. Тогда их оценками будут средняя приростов 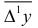 у и статистическая дисперсия
у и статистическая дисперсия
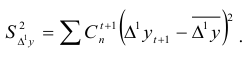
Применив неравенство Чебышева, можно записать:
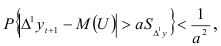
где 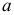 — заданное положительное число;
— заданное положительное число;
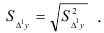
Так как значения 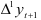 коррелированны между собой, то а в неравенстве Чебышева является величиной переменной, вычисляемой по формуле
коррелированны между собой, то а в неравенстве Чебышева является величиной переменной, вычисляемой по формуле
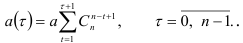
Прогнозирование методом гармонических весов производится путем прибавления к последнему значению ряда динамики 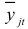 среднего прироста
среднего прироста
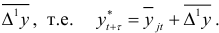
Доверительный интервал прогноза имеет вид:

Пример 9.5.
Рассмотрим динамический ряд, характеризующий производство цемента (см. таблицу 9.5). Этот динамический ряд не имеет скачкообразных изменений и достаточно хорошо описывается линейным трендом. Поэтому для дисконтирования уровней ряда динамики с целью определения прогноза производства цемента в 1991 г. применим метод гармонических весов. Построим вначале скользящий тренд. Для этого разобьем исходный ряд динамики на интервалы, каждый из которых содержит 5 уровней. Для каждого интервала скольжения строим методом наименьших квадратов линейный тренд
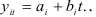
Так, первый интервал скольжения состоит из уровней 122, 124, 127, 127, 123, то система нормальных уравнений для оценки параметров, имеет вид
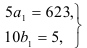
откуда находим
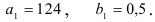
Следовательно, линейный тренд для первого интервала скольжения выражается уравнением

Аналогично определяем параметры уравнений для всех
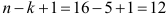
интервалов скольжения:

С помощью построенных уравнений определим значения 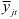 скользящего тренда по формуле (9.11).
скользящего тренда по формуле (9.11).
При 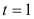 имеем
имеем
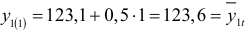
При 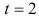 имеем два значения функций, для которых:
имеем два значения функций, для которых:
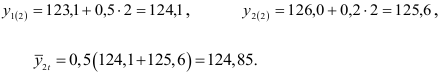
Аналогично находим все остальные значения 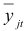 :
:
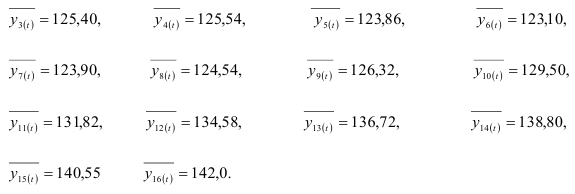
Проверим теперь гипотезу о том, что отклонения 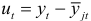 от скользящего тренда имеют случайный характер. Для этого вычислим нормированную автокорреляционную функцию (9.12) для
от скользящего тренда имеют случайный характер. Для этого вычислим нормированную автокорреляционную функцию (9.12) для 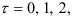 Значения автокорреляционной функции для
Значения автокорреляционной функции для 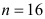 равны:
равны:
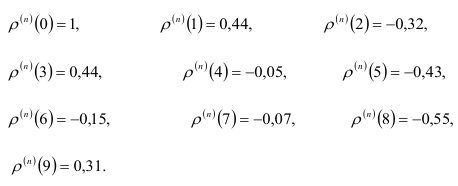
Значения автокорреляционной функции для 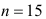 после исключения первого отклонения будут равны:
после исключения первого отклонения будут равны:
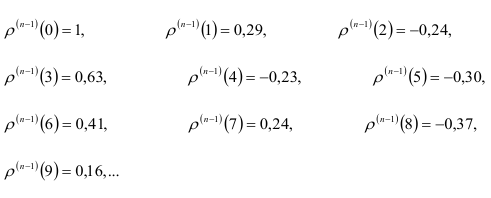
Пусть 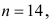 тогда:
тогда:
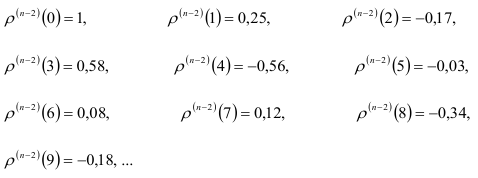
Отметим, что для 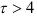 значения коэффициентов автокорреляции можно подвергать сомнению. Но для подтверждения убывания коэффициентов автокорреляции вычисление проводилось до значения
значения коэффициентов автокорреляции можно подвергать сомнению. Но для подтверждения убывания коэффициентов автокорреляции вычисление проводилось до значения 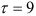 . И тогда, с уверенностью, можно утверждать, что значения автокорреляционной функции постоянно затухают. Проверим однородность коэффициентов автокорреляции. Для этого вычислим
. И тогда, с уверенностью, можно утверждать, что значения автокорреляционной функции постоянно затухают. Проверим однородность коэффициентов автокорреляции. Для этого вычислим 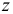 критерий:
критерий:
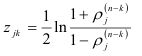
и 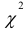 по формуле (9.13). Значения
по формуле (9.13). Значения 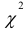 для трех групп коэффициентов автокорреляции равны:
для трех групп коэффициентов автокорреляции равны:
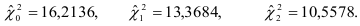
Вычисленные значения меньше табличного 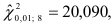 , следовательно, с вероятностью
, следовательно, с вероятностью 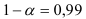 можно утверждать, что отклонения от тренда образуют стационарный в широком смысле случайный процесс. Затем вычисляем приросты по формуле
можно утверждать, что отклонения от тренда образуют стационарный в широком смысле случайный процесс. Затем вычисляем приросты по формуле 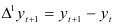 :
:

и гармонические веса 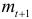 :
:
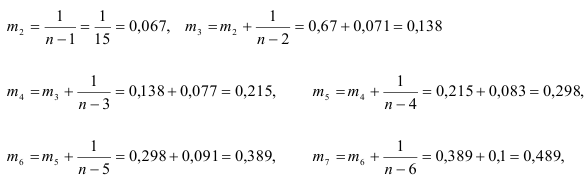
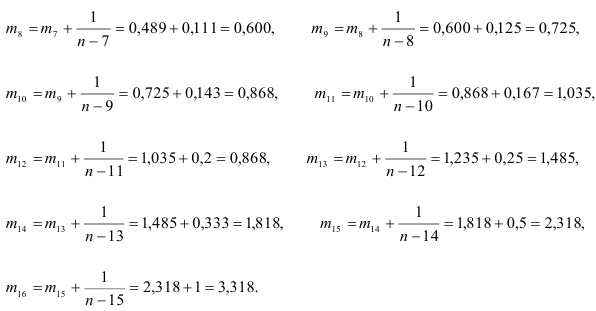
Гармонические коэффициенты вычисляем по формуле 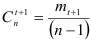 :
:
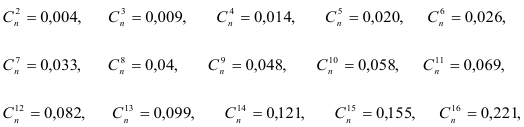
Все эти коэффициенты положительны, их сумма равна единице. Найдем средний прирост:

Тогда прогноз производства цемента на 1991 г. равен:
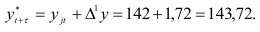
Для построения доверительного интервала вычислим среднее квадратичное отклонение:
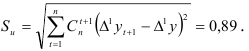
Найдем функцию
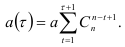
Так как
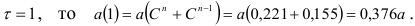
Произведение
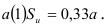
Пусть
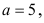
тогда вероятность того, что прогноз производства цемента выйдет за пределы доверительного интервала, не превосходит 0,04, что следует из неравенства Чебышева 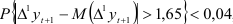 , так как
, так как 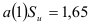 . Доверительный интервал имеет вид:
. Доверительный интервал имеет вид:
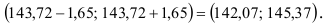
Еще раз подчеркнем, что метод гармонических весов применяется, когда в ряду динамики отсутствуют сезонные и циклические колебания.
Следовательно, мы спрогнозировали только значение детерминированной компоненты динамического ряда.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

