Оглавление:
Прогнозирование динамики социально-экономических явлений по трендовым моделям
Прогнозирование с помощью трендов — также один из простейших и распространенных методов статистического прогнозирования. Суть этого метода заключается во временной экстраполяции. При этом предполагается, что:
- период, для которого построен тренд, достаточен для выявления тенденции;
- анализируемый процесс устойчив и обладает инерционностью;
- не ожидается сильных внешних воздействий на изучаемый процесс, которые могут серьезно повлиять на тенденцию развития.
При соблюдении этих условий экстраполяция осуществляется путем подстановки в уравнение тренда значения независимой переменной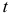 
, соответствующей периоду упреждения (прогноза). Получается точечная оценка прогнозируемого показателя (в конкретном году, квартале, месяце, дне) по уравнению, описывающему тенденцию. Полученный прогноз является средней оценкой для прогнозируемого интервала времени, так как тренд характеризует некоторый средний уровень на каждый момент времени. Отдельные наблюдения, как правило, отклоняются от него в прошлом. Естественно ожидать, что подобные отклонения будут происходить и в будущем. Поэтому определяется область, в которой с определенной вероятностью следует ожидать прогнозируемое значение, т. е. вычисляется доверительный интервал:
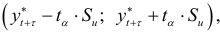
где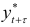 
— точечный прогноз на момент 
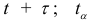— табличное значение 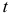-критерия Стьюдента с 
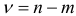степенями свободы при уровне доверия 
; 
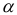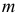— число параметров тренда; 
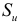— средняя квадратичная ошибка тренда:
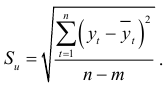
В основу расчета доверительного интервала прогноза положен показатель, определяющий колеблемость ряда заданных значений признака. Чем выше эта колеблемость тем менее определено положение тренда и тем уже должен быть интервал для вариантов прогноза при одном и том же уровне доверия. В качестве такого показателя ряда наблюдаемых значений признака обычно рассматривается среднее квадратичное отклонение фактических наблюдений от расчетных, полученных при выравнивании динамического ряда, т. е. средняя квадратичная ошибка тренда.
Доверительный интервал (9.1) учитывает неопределенность, связанную с положением тренда. Но он должен учитывать также и возможность отклонения от тренда, т. е. среднюю квадратичную ошибку прогноза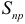 
.
Тогда доверительный интервал прогноза будет иметь вид
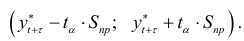
Стандартная ошибка прогноза, когда тренд описывается прямой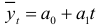 
, вычисляется по формуле:
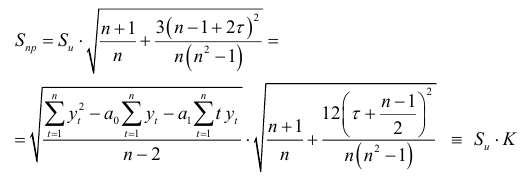
и доверительный интервал (9.2) примет вид
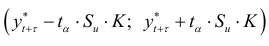
где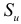 
— среднее квадратичное отклонение фактических уровней динамического ряда от расчетных, называемая стандартной ошибкой тренда; 
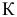— величина, зависящая только от длины динамического ряда и периода упреждения 
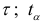— табличное значение 
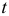— критерия Стьюдента с 
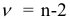степенями свободы при уровне доверия 
.
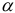С увеличением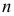 
значения 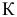уменьшаются, а с увеличением 
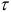-увеличиваются. Поэтому достаточно надежный прогноз получается при относительно большом числе наблюдений (для линейного тренда 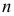= 6, для параболического второй степени 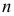= 13, для кубического 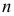= 23), когда период упреждения не очень большой. При одном и том же 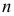с ростом 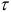доверительный интервал прогноза увеличивается. Кроме того, доверительный интервал прогноза при одной и той же величине средней квадратичной ошибки 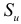будет тем шире, чем выше степень полинома, характеризующего тренд.
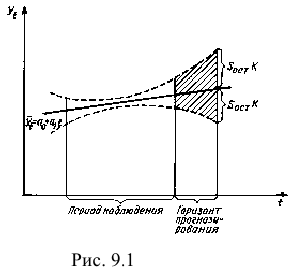
Доверительные интервалы для линейного тренда, изображены на рис. 9.1.
Проиллюстрируем нахождение прогноза по уравнению тренда и построение доверительного интервала на примере.
Пример 9.2.
Рассмотрим динамический ряд, характеризующий производительность труда с февраля 1988г. по апрель 1989г. (см. пример 3.7). Для данного ряда наилучшей функцией, характеризующей тренд, была признана прямая
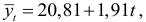
поэтому прогностическая модель имеет вид
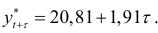
Прогнозирование с помощью этой модели осуществляется весьма просто: необходимо вместо 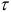в уравнение подставить нужное значение и найти прогноз. Так, для прогнозирования производительности труда в апреле 1989г. нужно подставить 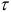= 15, вследствие чего
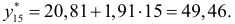
Если прогноз необходимо сделать в году 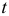, а период упреждения равен 
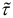, то в прогностическую модель подставляется значение 
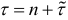, где 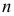= 14 соответствует марту 1989г. Доверительные интервалы найдем, используя выражение (9.3). Необходимые для этого значения 
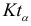можно определить из соответствующей таблицы (см. [19,прил. 7]). Результаты вычислений сведены в табл. 9.2.
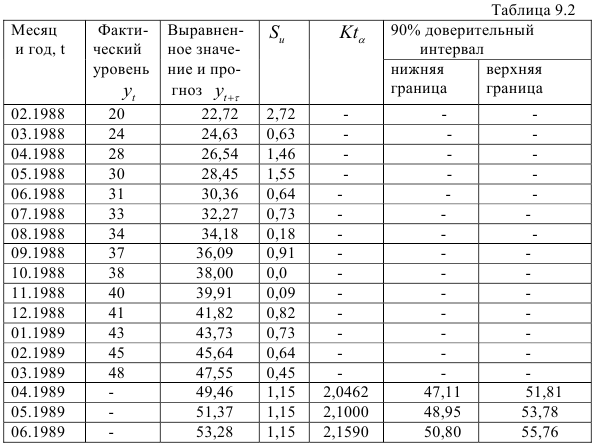
Среднее квадратичное отклонение равно 1,15. Из таблицы видим, что доверительные интервалы оказались достаточно широкими — свыше 9% прогнозируемого уровня.
Этот пример показывает, что экстраполяция по тренду — достаточно грубая операция, основывающаяся на целом ряде допущений.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:
