Оглавление:
Проекции вектора на ось и на плоскость
Аналитический способ решения задач статики основан на применении метода проекции, знакомого студентам из векторной алгебры. Ввиду особой важности этого метода для дальнейшего, напомним его основы.
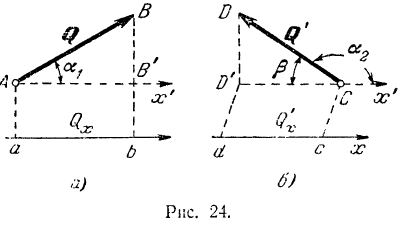
Проекцией вектора на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка оси проекций, заключенного между проекциями на нее начала и конца данного вектора (рис. 24).
Проекция считается положительной, если переход от ее начала к концу совпадает с заданным положительным
направлением оси, и отрицательной — если с противоположным.
Проекцию вектора на ось принято обозначать теми же буквами, что и вектор, но обычного шрифта, указывая нижним индексом ось проекций.
Проекции вектора на две параллельные и одинаково направленные оси равны между собой. Этим особенно удобно бывает пользоваться в тех случаях, когда вектор не лежит в одной плоскости с осью (рис. 24,(5). Из рис. 24, а и б имеем:
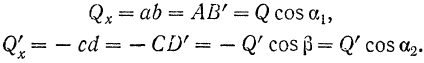
Проекция вектора на ось равна модулю вектора, умноженному на косинус угла между направлением вектора и положительным направлением оси проекций
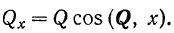
Проекция будет положительной, если направление вектора составляет с положительным направлением оси острый угол, н отрицательной — если тупой.
Проекцией вектора на плоскость называется вектор, заключенный между проекциями на эту плоскость начала и конца данного вектора.
Так, например, проекцией_вектора 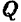 на плоскость
на плоскость 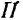 (рис. 25) будет вектор
(рис. 25) будет вектор 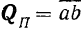 .
.
По модулю проекция вектора на плоскость:
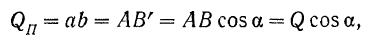
где 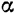 — угол между направлением вектора
— угол между направлением вектора  и направлением его проекции
и направлением его проекции 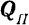 на плоскость.
на плоскость.
Для нахождения проекции вектора на ось, не лежащую с ним в одной плоскости, иногда бывает удобно
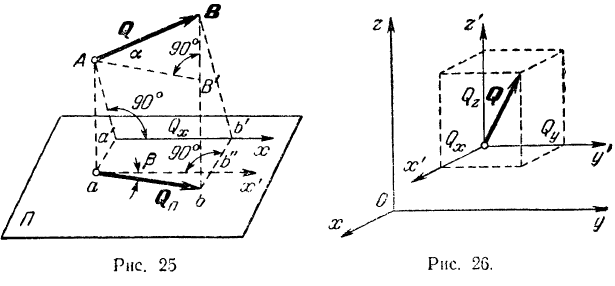
спроектировать сначала вектор на плоскость, в которой лежит эта ось, а затем уже проекцию вектора на плоскость спроектировать на данную ось.
Так, проекция вектора 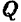 на ось
на ось 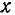 (рис. 25):
(рис. 25):
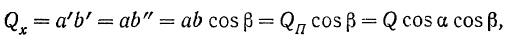
где 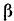 — угол между направлениями вектора
— угол между направлениями вектора 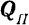 и оси
и оси 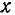 .
.
Зная проекции вектора па оси прямоугольной декартовой системы координат, легко найти и модуль и направление вектора.
Так как модуль вектора равен диагонали прямоугольного параллелепипеда (рис. 26), ребра которого равны абсолютным значениям проекций вектора на оси координат, то модуль вектора
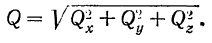
Модуль вектора равен квадратному корню из суммы квадратов его проекций на три любые взаимно перпендикулярные оси.
Направление вектора определяется из равенств:
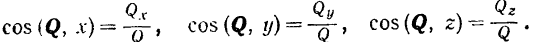
Косинус угла между вектором и положительным направлением оси проекции называется направляющим косинусом. Он равен отношению проекции вектора на соответствующую ось к модулю вектора.
Заметим, что в формуле (4) надо брать арифметическое значение корня.
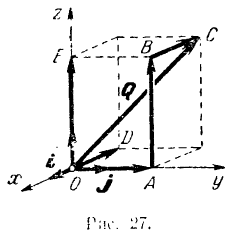
Вектор 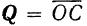 (рис. 27) является замыкающем стороной векторного многоугольника
(рис. 27) является замыкающем стороной векторного многоугольника 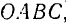 , следовательно его можно рассматривать как геометрическую сумму составляющих векторов, расположенных па координатных осях
, следовательно его можно рассматривать как геометрическую сумму составляющих векторов, расположенных па координатных осях
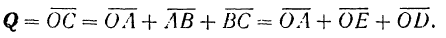
Век горы 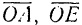 и
и 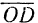 называются составляющими вектора
называются составляющими вектора 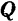 но осям координат (или его компонентами).
но осям координат (или его компонентами).
Векторы 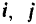 и
и 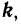 совпадающие с положительными направлениями координатных осей и равные по модулю единице, называются единичными координатными векторами или координатными ортами соответствующих осей.
совпадающие с положительными направлениями координатных осей и равные по модулю единице, называются единичными координатными векторами или координатными ортами соответствующих осей.
Составляющая вектора по оси координат равна проекции вектора на данную ось, умноженной на соответствующий координатный орт:
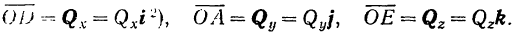
Подставляя последние выражения в предыдущее равенство. получаем весьма важную формулу разложения вектора по осям координат
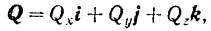
где коэффициенты 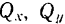 и
и 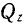 при координатных ортах представляют собой проекции данного вектора на соответствующие координатные оси.
при координатных ортах представляют собой проекции данного вектора на соответствующие координатные оси.
Пример задачи:
Даны проекции силы на оси прямоугольной системы координат
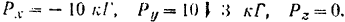
Написать формулу разложения заданной силы по осям координат, а также найти ее модуль и направление.
Решение:
По формуле 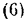 находим
находим
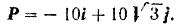
Модуль силы
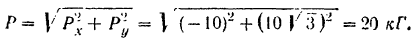
Направляющие косинусы
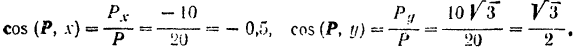
Отсюда, углы между направлением силы и положительными направлениями осей координат:
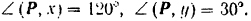
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

