Проекции ускорения на оси естественного трехгранника

Проекции ускорения на оси естественного трехгранника

Как мы уже заметили, при движении точки по окружности ее ускорение может быть представлено в виде двух составляющих, одна из которых направлена по касательной к окружности, а другая к центру окружности. При движении точки по произвольной кривой в каждый момент времени достаточно малый участок траектории можно рассматривать как часть дуги окружности соответствующего радиуса, а непрерывное движение точки по траектории можно представить как некоторую последовательность движений по дугам соответствующих окружностей.

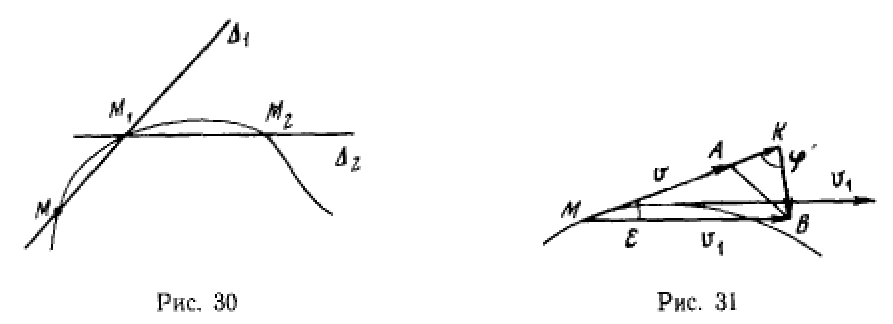
Рассмотрим три последовательных положения точки на траектории: 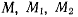(рис. 30). Если точка 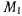занимает бесконечно близкое положение по отношению к точке М, то отрезок 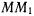в пределе определит положение касательной к кривой в
точке М. Если траектория не является прямой линией, то три точки 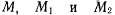определят некоторую плоскость. Предельное положение этой плоскости, когда точки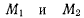

неограниченно стремятся к точке М будем называть соприкасающейся плоскостью в точке М. Касательная к кривой, построенная в точке М, лежит в этой плоскости. В общем случае три точки 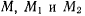однозначно определяют окружность

лежащую в соприкасающейся плоскости. Предельная окружность, получающаяся при неограниченном приближении точек 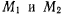к точке М, называется окружностью кривизны, или кругом кривизны. Радиус этой окружности называют радиусом кривизны. Круг кривизны всегда находится в соприкасающейся плоскости. Хорды 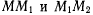в пределе, при неограниченном приближении точек 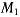к точке 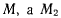к точке 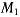определят касательные к кривой в точках 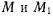соответственно (рис. 30), а следовательно, и направление скоростей в этих точках.

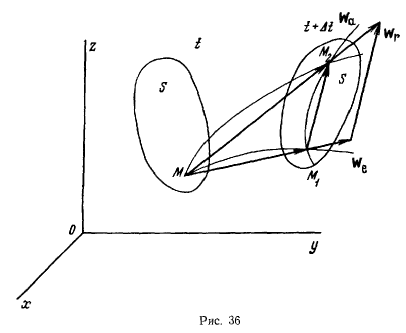
Обозначим скорости точки в положениях 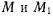соответственно через 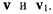Перенесем 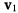в точку М (рис. 31).
Два вектора 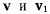определят плоскость. Предельное положение этой плоскости, когда точка 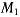неограниченно приближается к точке М, будет определять соприкасающуюся плоскость. Вектор 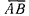определяет перемещение индекса скорости по годографу. Геометрическая величина вектора 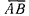определится из равенства

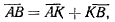
где точки 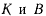лежат на одной и той же окружности с центром
в точке М (рис. 31). Разделим это равенство на

Отношение 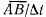равно среднему ускорению точки М за время 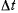Ускорение точки М является предельным значением среднего ускорения, когда интервал времени 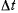неограниченно стремится к нулю.

Рассмотрим вектор 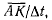который всегда направлен по касательной к траектории. Предельное значение модуля этого вектора будет иметь вид

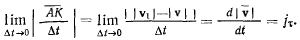
Производную по времени от модуля скорости точки назовем касательной, или тангенциальной, составляющей ускорения точки. Можно еще ввести в рассмотрение вектор касательного ускорения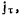

положительное направление которого совпадает с направлением скорости точки, а величина равна производной от модуля скорости точки. Обозначив через 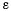угол между направлениями скоростей 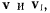назовем этот угол углом смежности (рис. 32). Тогда для предельного значения модуля вектора 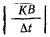получим

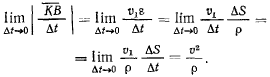
Здесь как это видно из чертежа, представляет собой длину дуги траектории, соединяющей точки Предельное значение величины отрезка когда точка неограниченно приближается к М, назовем радиусом кривизны траектории в точке М

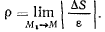
Обозначив через 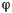угол 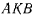(рис. 31), получим

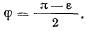
Предельное значение этого угла, когда 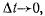равно 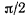следовательно,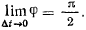

Предельное значение вектора 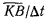обозначим через 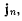т. е.

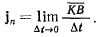
Величина этого вектора равна отношению квадрата скорости точки
к радиусу кривизны траектории, 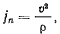сам вектор лежит в соприкасающейся плоскости и направлен ортогонально к скорости точки в сторону вогнутости траектории. Та нормаль 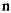к траектории, которая лежит в соприкасающейся плоскости и направлена в сторону вогнутости траектории, называется главной нормалью, а вектор направленный по главной нормали к траектории, называется нормальным ускорением точки (рис. 33).

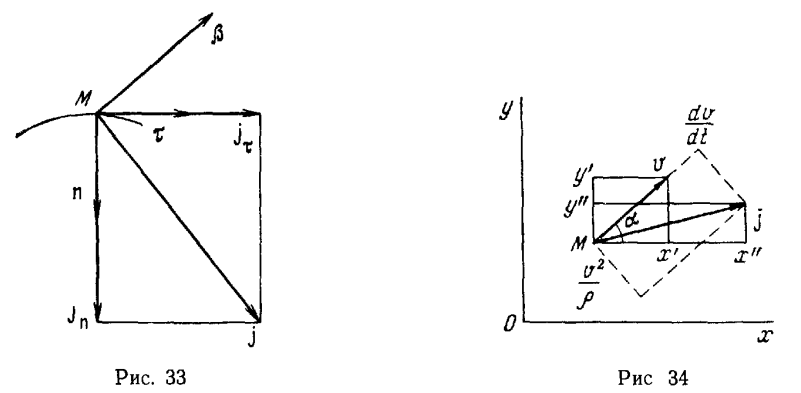
Рассмотрим систему осей координат с началом в точке ось 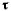направим по касательной к траектории точки, ось 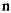по направлению главной нормали, а третью ось 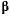(по бинормали) направим так, чтобы тройка векторов 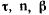образовала правую систему.
Выбранные так оси представляют собой сопровождающий трехгранник, который еще называют естественным трехгранником. Проекции ускорения на оси естественного трехгранника равны

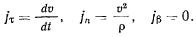
Модуль ускорения определяется равенством

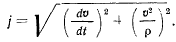
Пример:

Точка движется по плоскости по закону

Определить радиус кривизны траектории точки.

Решение:

Величины скорости и ускорения определяются из формул

Касательную составляющую ускорения найдем, дифференцируя квадрат скорости точки

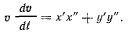
Вычислим радиус кривизны траектории точки по формуле

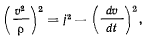
или

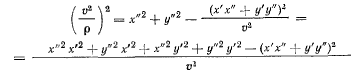
Приводя подобные члены и умножая на 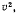получим

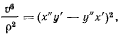
откуда

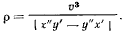
Можно дать и геометрическое решение этой задачи. Как видно из рис. 34, проекция ускорения на нормаль к траектории равна

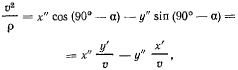
откуда сразу же следует выведенная выше формула для радиуса кривизны траектории.

Пример:

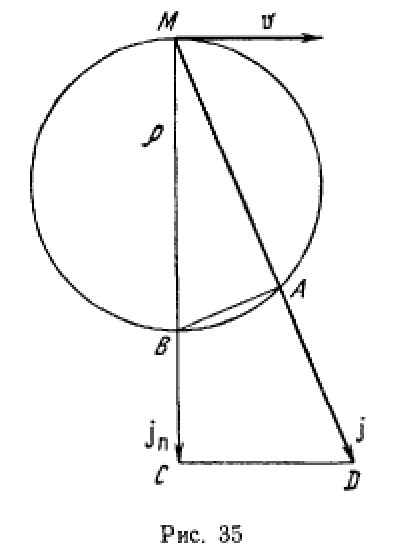
Точка описывает плоскую траекторию. Линия действия ее ускорения в пересечении с кругом кривизны образует хорду 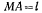(рис. 35). Выразить величину ускорения точки через величину ее скорости и длину этой хорды

Решение:

Из подобия треугольников 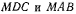следует

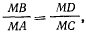
откуда получим

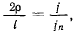
или

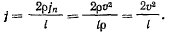
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:

Предмет теоретическая механика

Эти страницы возможно вам будут полезны:

Скорость и ускорение точки в полярных координатах

Движение точки по окружности

Теорема о сложении скоростей в сложном движении точки

Метод Роберваля построения касательных к плоским кривым