Проекции

Проекции

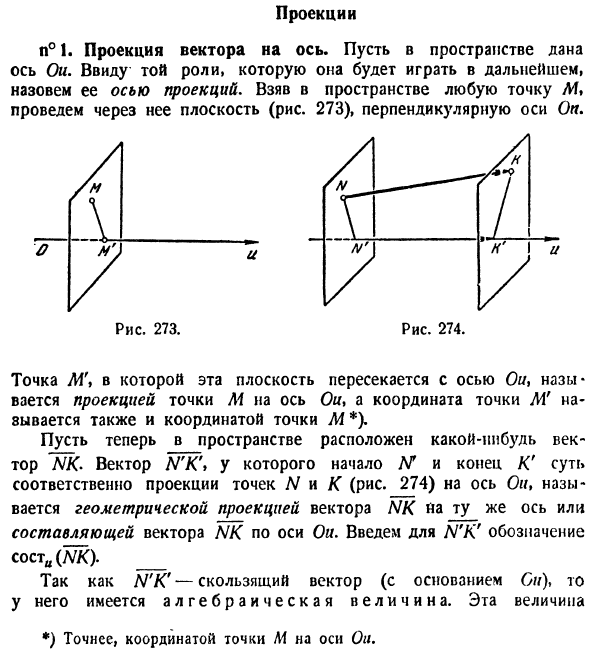
• проекция n ° 1. Проекция вектора на ось. Отдайте ось Oi в пространстве. Учитывая роль, которую он будет играть в будущем, мы называем это осью прогнозирования. Получите произвольную точку / Vf в пространстве и нарисуйте плоскость, перпендикулярную оси On (Рисунок 273). и Рисунок 274. Рисунок 273. Точка M \, где эта плоскость пересекает ось Oi>, называется проекцией точки M на ось He, а координаты точки M также называются координатами точки M ). Теперь предположим, что некоторые векторы NK находятся в пространстве.

Вектор N’K ‘, чьи начало N и конец K’ являются проекциями точек N и K на ось He (рис. 274) соответственно, является геометрией компонентов вектора NK вдоль той же оси или оси He, что и вектор NK Это называется статической проекцией. N’K ‘Введено обозначение кости (NK). _ N’K ‘имеет алгебраическую величину, потому что имеет скользящий вектор (основание Ои . Эта величина *) Точнее, координаты точки М на оси He.

Называется алгебраической проекцией вектора NK на ось Oy. Отныне мы будем называть только эту проекцию Для проекции вектора NK на ось O и геометрической проекции № K сохраняется только имя компонента. Итак, для нас: Проекция вектора NK на ось Oy показывает числовое значение. 0) // Если C = al. Это привело. (Comp ^ L / K). Понятно, что , и 2) проекции векторов на две параллельные и одинаковые оси направления равны. № 2. Самое важное свойство проекции. Теорема.

проекции двух равных векторов на одну и ту же ось равны Людмила Фирмаль

Умножение числа на вектор умножит эту проекцию на это число. (2) Когда (Па) = р То есть числовой коэффициент может быть создан как третий признак проекции. На самом деле, пусть а = нк. Если p> 0, умножение NK на p сохраняет направление вектора NK и расширяет его в p раз ^ Если p <1, оно увеличивается в p раз *, сокращается до | Из чертежа *) ясно, что то же самое происходит с компонентом № K ‘= cocruNK *. То есть умножение вектора на число p> 0 также умножит этот компонент на это число. То же самое верно для р <0. Вот так Состояние (pa) = p, но затем (по теореме 2 § 1 № 6) Водоросли Вел. [sost (ra)] = R. alg. Скорость (Компаратор)

Это определение самой проекции [Ref (1) из n ° 1] является точным доказанным уравнением (2). Теорема 2. Проекция вектора на оси координат равна координатам конечной точки, исключая координаты начальной точки. (3) Pr TU K = ir ~ -и l’- *) Предоставьте читателям это сделать.

• Фактически, если coctuNK = LTK ‘, _ существует по теореме 3§1 из n ° 6. PrM (= alg. Vel. N ‘K’ = и / c- «lg. Определяя точно координаты точки, которая не находится на оси, ik> = ik> и n, = un- Теорема 3 * Проекция суммы нескольких векторов на ось равна сумме проекций слагаемых на одну ось. (4) Prv (fli + … + ap) = Pr. *, + … + пр. Например, докажем теорему о = 4. Определив векторную сумму, построим любую точку в пространстве A0, затем положим вектор A0AX = ai, затем A в A \ Ai = ab, затем положим L3 = a3 и ArAk = a ^ Вектор s = A ^ Ak и общее число ++

Предполагая, что ось проекции Oy является координатной осью (то есть предполагается, что существует числовая метка), координаты точек A & A \ и A * Ai обозначены как u0, Hi »uit,% и w4 соответственно. Далее, согласно предыдущей теореме, npttfli = wi и » PraA3 = «3- Великий «4-UK для UIF Откуда Прая, + Pral * + Praa3 + Pr, 4aA = uL-u0. Также обратите внимание, что Prl «равен UL- Теорема 4. Проекция разности двух векторов на любую ось равна разности их проекций на одну ось.

Прямой (a- *) = Прва-ПрА Пусть a-b = r. Тогда a = b + j и (4) Пуллер = Pr / <6 + Pr1.l Это эквивалентно (5). Теорема 5. Проекция вектора равна длине, умноженной на косинус угла между вектором и осью проекции. Доказательство. Параллельная передача проецируемых векторов не меняет проекцию. Таким образом, мы можем предположить это (5)

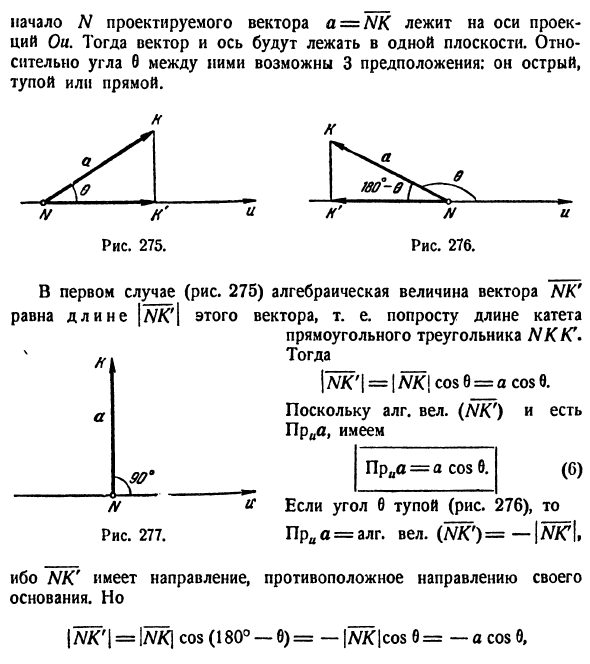
. Во-вторых, вектор и ось находятся в одной плоскости. Что касается угла 0 между ними, возможны три предположения: оно острое, тусклое или прямое. В первом случае (рис. 275) алгебраическая величина вектора NK Длина этого вектора \ NK ‘\, то есть просто равна длине ноги Прямоугольный треугольник NK / C тогда \ U ‘\ — \ NK \ cos B-cos 6. H / V Рисунок 277. С тех пор.

Начало N вектора проекции a = NK находится на оси проекции Oi Людмила Фирмаль

Это привело. (NK ‘) это Приа. (С) Praa = a cos b. # Когда угол e тупой (рис. 276), когда a = al. Это привело. (НК ‘) = — | Л7С |, НК имеет противоположное направление к своей базе. но jyvK’l = | 7V / q cos (180 ° -6) = — | N / C | cos0 = -a cosО,И снова перейдите к (6). Наконец, уравнение (6) также применимо, когда 6 = 90 ° (рис. 277). В этом случае обе части равны нулю. Теорема полностью доказана.

Смотрите также:

Предмет высшая математика

Решение систем линейных уравнений	Координаты в пространстве
Векторы	Скалярное произведение векторов