Оглавление:


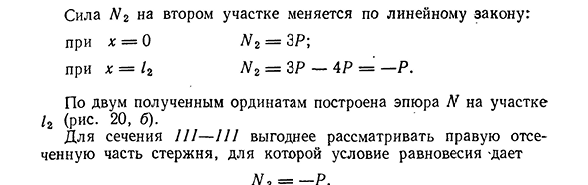

Продольные силы и их эпюры
- Продольная сила и ее контур Растяжение и сжатие очень распространены в строительных конструкциях и механических элементах. Например, происходит натяжение троса — подъемный трос (рис. 16, а), буксирный трос — при буксировке автомобиля, вес заводской трубы (рис. 16, б), колонна, поддерживающая потолок, и т.
Д. В зависимости от того, как зафиксирован шток и от характера влияния нагрузки, могут возникать различные типы растяжения или сжатия. Если внутренняя сила поперечного сечения стержня уменьшается только до одного фактора силы —
продольной силы N (также называемой нормальной силой, потому что она Людмила Фирмаль
перпендикулярна поперечному сечению стержня), и О) б) Рисунок 16 А Поскольку оставшаяся внутренняя сила равна нулю, происходит чистое (центральное) расширение или сжатие. В этой главе рассматривается только центральное действие продольных сил. Другие более сложные случаи расширения или сжатия описаны в разделе. Xi. Внешние силы, которые вызывают растяжение или
сжатие, приложенные к концу или середине стержня, также должны быть направлены вдоль этой оси или уменьшены до результата, направленного вдоль этой оси. Чтобы определить продольную силу, стержень мысленно рассекают плоскостью, перпендикулярной оси стержня, и заменяют двумя продольными силами N, а две части из равновесия являются значениями этой силы Это зависит от Мы
- согласны думать, что сила N положительна, если она вызывает натяжение (ведущее от сечения), и отрицательна, если она вызывает сжатие (ведущее к сечению). Части. Часть взаимодействия между Рисунок 17 А Если направление силы N неизвестно, мы рекомендуем положительное значение. Если при решении уравнения равновесия сила N получена со знаком плюс, стержень в этом разделе будет растянут, а при наличии знака минус он будет сжат. Так, например, чтобы определить нормальную силу сечения стержня m-n, показанного на рисунке, рассмотрите баланс левой части зажима 17а (рис. 17, б). Создание уравнения £ X = 0, D ‘-P = 0; N = + P Знак плюс
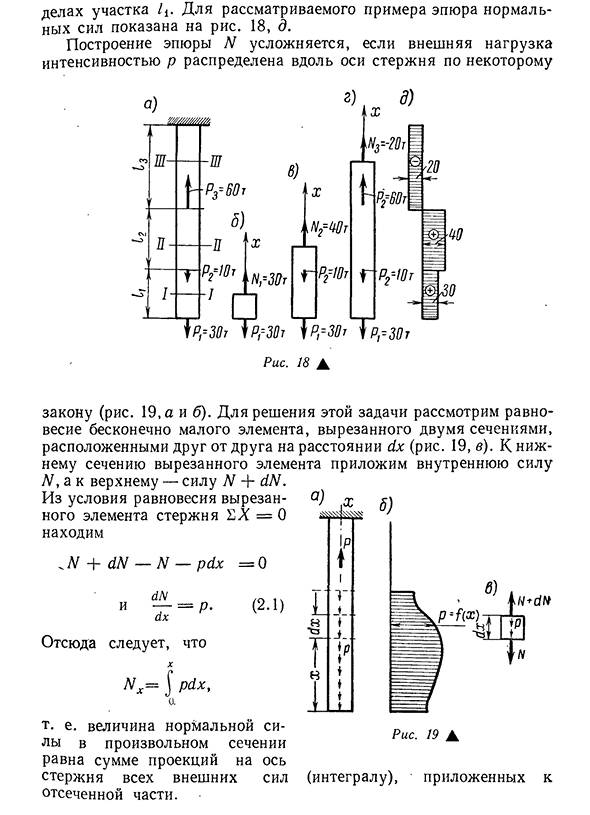
означает, что вал выдвинут. Если сложно, рекомендуется построить прозрение внутренне и в х с и л. Диаграмма продольной силы N представляет собой график, где каждая ордината равна значению продольной силы для определенного сечения. Сюжет обычно строится на базовой линии, проведенной параллельно оси стержня. Чтобы построить кривую N, необходимо установить закон изменения продольной силы вдоль длины стержня и определить значение N нескольких поперечных сечений. Поэтому для стержня, показанного на рисунке 18a, нормальные силы в сечениях / b / 2 и / 3 различны
на рисунке 18a. Это установлено с учетом равновесия отсечки, показанного на рисунке 18. 18, b, c, d Применение статическог Людмила Фирмаль
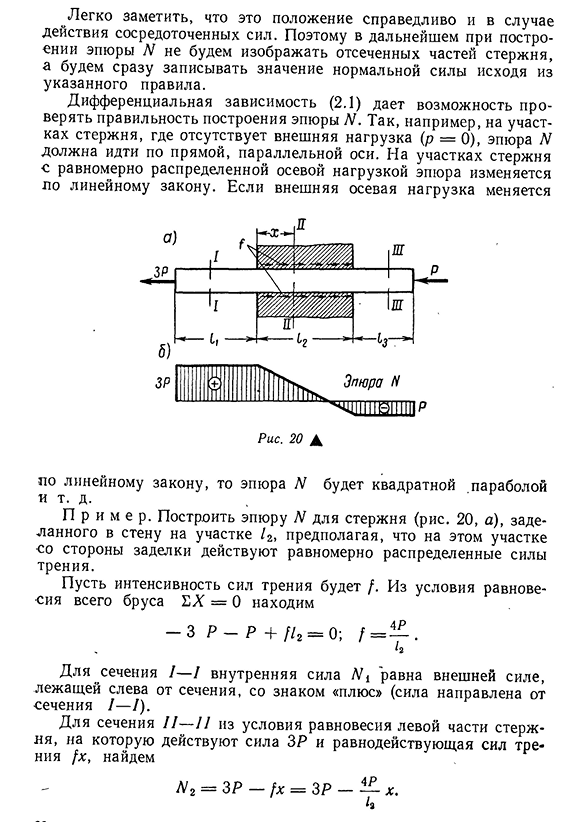
о уравнения EL = O к этим частям дает Nt-30 T, N 2 = 40T и N 3–20 T. Поскольку нормальная сила не изменяется по длине каждого участка, условие равновесия отрезанной части, значение нормальной силы Ni, например, сечение I — I График нормальной силы показан на рисунке для примера, который рассмотрел 20 случаев / Р на графике. 18, д. График N является сложным, если внешняя нагрузка с силой р распределена вдоль оси стержня. Закон (рис. 19, а и б). Чтобы решить эту проблему, рассмотрим равновесие микроэлементов, разрезанных двумя сечениями на расстоянии dx друг от друга (рис. 19, в). Внутренняя сила N прикладывается к нижней части режущего элемента, а сила N + dN применяется к верхней части. Из состояния равновесия S X = О элемента выреза стержня, + dN-N-pdx = O о, о И- = р. (2.1) о X N x-J pdx, ок. Другими словами, величина нормальной силы в любом сечении равна сумме проекций всех внешних сил в отсечной части на ось стержня. Рисунок 19 А Применяется к (интеграция) 21
Легко видеть, что это верно даже в случае концентрации. Поэтому в будущем, когда вы будете наносить N, вы не увидите отрезанную часть стержня, а сразу запишите значение нормальной силы, основанное на указанных правилах. Точность графика N можно проверить с помощью дифференциальной зависимости (2.1). Например, в секции стержня без внешней нагрузки (p = 0) участок N должен быть прямой линией, параллельной оси. На участке стержня, где осевая нагрузка равномерно распределена, график изменяется
линейно. Когда внешняя осевая нагрузка изменяется Рисунок 20 А [-F H | «Я 1LG к-т (- * + * тг * ■ * 1 А • Вт / Согласно линейному закону диаграмма N представляет собой квадратную параболу. Создайте схему N стержня (рис. 20, а), встроенную в стену в П р и м е р с. / 2. В этом разделе предполагается, что сила трения равномерно распределена на стороне погружения. Сила силы трения равна /. CA EX = 0-3 P-P + [12 = 0; 2 Для секции / -1 внутренняя сила равна внешней силе на левой стороне секции со знаком плюс (сила направлена от
секции I- /). В случае с разделом f / — // N2 = 3P-fx = 3P-˜x. ^ 2 22 Сила второго сечения / V2 изменяется линейно. х = ОН 2-ЗР ´, х = l2 Н 2-3П-4Р = —Р. Используя две полученные ординаты, график IV был построен на графике / 2 (рис. 20, б). В разделах 111-111 выгодно рассмотреть отрезанную часть на правой стороне стержня, заданную условиями равновесия. N 3 = -P-
Смотрите также:

