Оглавление:






Процессы, связанные с изменением агрегатного состояния или химической природы вещества
- Предварительные замечания. Когда свободная поверхность воды охлаждается до 0°C, из-за аномального температурного хода плотности воды получается стабильное распределение. Вода при 0°с легче, чем — + 4°С, и поэтому слой имеет разную температуру. Поэтому нет никаких оснований для конвекции и, соответственно, образования льда в будущем. Термическое удаление можно рассматривать как процесс с помощью чистой теплопроводности. Другие процессы затвердевания и любое замораживание 2 > растворить с ингредиентами.*). Кроме того, сюда следует добавить процессы, связанные с химическими реакциями(например, сжигание извести). Наконец, проблема, диффузия веществ в твердых телах с химическими реакциями.
Когда достигается определенная концентрация, молекулы диффузии химически Он связывается и, следовательно, блокируется от процесса диффузии⁶). Для наших целей существенные особенности этих процессов можно свести к следующим 4 функциям: 1)происходит изменение химических свойств среды в соответствии с агрегатным состоянием или полем. 2) в результате выделяется (поглощается) тепло фазы теплового или химического превращения. 3) в месте, где происходит фазовое или химическое превращение, значения физических констант X, c и p резко меняются. 4) конвекция отсутствует вообще. B. замораживание влажной почвы. 。Влажная почва в первый момент процесса имеет температуру БТС по всему своему объему.
В области пузырчатого кипения было принято, что движение пузырьков является доминирующим фактором для процесса теплообмена. Людмила Фирмаль
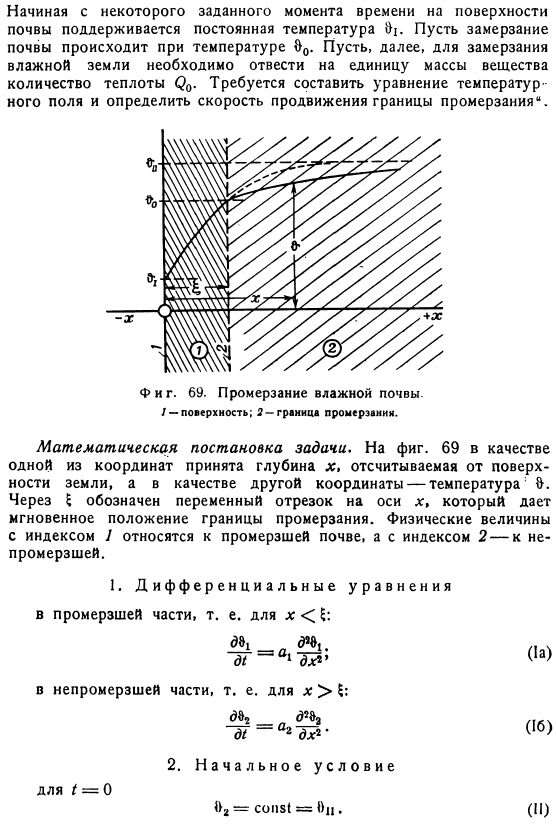
Эти соображения нельзя считать строгими. При рассмотрении теплового коэффициента как переменной величины описываются основные члены, определяющие теплопередачу по проводимости. див(х град 9)= ХV * 9 + х Град Град 9. Начиная с заданного момента времени, на поверхности почвы поддерживается постоянная температура 9j. Замораживают почву при температуре 8°С. Далее、 Необходимо принять мерзлоту влажного грунта, количество теплоты Qₒ на единицу массы вещества. Вам нужно создать уравнение температуры- Математическая постановка задачи. Рис.
координаты берутся как 69, измеренная глубина x от поверхности Земли, а в качестве другой координаты-температура b E обозначает переменный сегмент на оси x и мгновенное расположение замороженной границы. Физическая величина индекса 1 относится к мерзлой почве, индексируемой 2 — не замораживать. 1.Дифференциальное уравнение Для замороженной части, а именно x E: 4.Процесс замораживания Согласно наблюдениям, если за время dt замерзшая граница продвигается на интервал di, следовательно, объем замерзшей массы Земли увеличивается на Fdi. Где F-это Заморозить границу section. In этот процесс, количество qtf> zfdi жары выпущен.
Очевидно, это и есть количество тепла-с теплом, исходящим от еще не замерзшего Грунт — надо брать через мерзлую землю. Следовательно, уравнение В полученном наборе условий (I) — (VI) температурная функция определяется однозначно. Решение проблемы problem. In Задача 5, Интеграл гауссовой ошибки оказался решением дифференциального уравнения. Если, C], Oc₁ и Cr, Dₜ — 4 произвольные константы、 Уравнение Является конкретным решением Формулы (1a)、 — Конкретное решение уравнения (16). 。 Если выполняются следующие условия, то выполняются условия (III) и (IV). 。 А потом наши личные решения Уравнение (1) дает значение 8r = «•при t =0, поэтому условие (II) также выполняется.
- Ток соответствует требованиям (V)для определения температуры замерзшей границы. если x = E, то уравнения (Vila) и (Villa) имеют вид. Это двойное уравнение должно быть выполнено для произвольно выбранного значения T. Однако О и О₂ являются константами, поэтому Интеграл ошибки Гаусса равен Постоянное значение. Однако это возможно только в том случае, если аргументы функции O остаются постоянными при изменении$с течением времени t. следовательно, сумма c Он должен меняться пропорционально Вт.
Если q-коэффициент пропорциональности、 Итак, если мы сделаем дифференциал относительно Γ、 Замораживание границ Получить скорость продвижения по службе Поначалу нетрудно заметить, что скорость продвижения очень велика (сначала она бесконечно велика), но затем она быстро уменьшается.
Небольшое увеличение теплового потока сверх этой величины, однако, заставляет подниматься температуру до тех пор, пока устанавливается новое условие равновесия немного выше точки С. Людмила Фирмаль
Далее, из двойного уравнения После подстановки значений как конкретного решения (Vila), так и (Villa), выберите формулу (1Xa) / care Для определения последней, которая является неизвестной константой, используйте условие (VI).У нас есть После подстановки этих значений производной выражения (VI) Используя уравнение (1X6) и b = Y Xer, получаем: Скорость проходки Таким образом, мы достигли трансцендентального уравнения с 1 неизвестным q. To решить ее лучше всего с помощью графических методов. Перепишите исходное уравнение в виде const q = function (q).Левая сторона определяет прямую линию через начало координат. Правая сторона показывает трансцендентальную кривую.
Свойства рассматриваемых линий таковы, что они всегда пересекаются в точке 1 point. So уравнение (X)всегда имеет 1 корень, и оно представлено корнем Q. присваивая формуле (1Xa) значение»q», находим мгновенное расположение замороженной границы. При введении ₀₀ в уравнения (vi16) и (vh16) определяется формат температурного поля. С помощью простых математических расчетов можно легко найти приближенные решения, которые могут помочь в количественной оценке. Предположим, что температура меняется. Замороженный слой по линейному закону.
Кроме того, в начале процесса замораживания предположим, что значение температуры всего объема было & had. In этот случай, только Теплота затвердевания по уравнению Напротив, E = 0 при t = 0 в начальном условии Для воды используют значения следующих физических констант: теплопроводность льда при 0°с= 1,9 ккал / М * время * °С. теплота плавления Qₒ= 79,4 ккал! плотность воды p,= 1000 кг / мг. Затем__________ Значение е выражается в метрах, которые должны заменить время Заметим, что приближенное решение по выражению (XI) содержит функцию времени точно такого же вида, как и точное решение (1Xa).Оба решения просто разные Количество постоянный вопрос.
Смотрите также:

