Проблема идентифицируемости модели. Необходимое и достаточное условие идентифицируемости
Изменение формы уравнений модели позволяет устранить проблему коррелированности факторных признаков и случайных отклонений, но может привести к другой проблеме -проблеме идентификации. Под идентификацией понимается возможность численной оценки параметров структурных уравнений по оценкам коэффициентов приведенных уравнений.
Исходную систему уравнений называют идентифицируемой (точно определенной), если по коэффициентам приведенных уравнений можно однозначно определить значения коэффициентов структурных уравнений. Однозначно определить коэффициенты структурных уравнений по коэффициентам приведенных уравнений можно в том случае, если количество уравнений, связывающих коэффициенты, равно количеству коэффициентов. Так, например, в модели Кейнса (6.6) — (6.7):
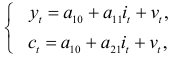
где
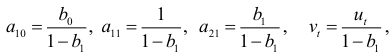
объем инвестиции 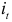 является экзогенной переменной и она не коррелирует со случайной составляющей. Это означает, что для случайной составляющей выполняются предпосылки МНК и оценки параметров
является экзогенной переменной и она не коррелирует со случайной составляющей. Это означает, что для случайной составляющей выполняются предпосылки МНК и оценки параметров 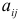 будут статистически значимыми. Зная
будут статистически значимыми. Зная 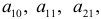 находим значения коэффициентов
находим значения коэффициентов 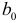 и
и 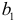 :
:
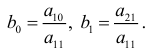
Следовательно, система (6.6) — (6.7) идентифицируема.
Исходную систему уравнений называют неидентифицируемой (недоопределеннойесли по коэффициентам приведенных уравнений можно получить несколько вариантов значений коэффициентов структурных уравнений. Это случай когда число уравнений, связывающих коэффициенты, меньше числа определяемых коэффициентов.
Исходную систему уравнений называют сверхидентифицируемой (переоопределенной), если по коэффициентам приведенных уравнений невозможно определить значения коэффициентов структурных уравнений. В этом случае система, связывающая коэффициенты, несовместна. Рассмотрим модель «спрос — предложение»
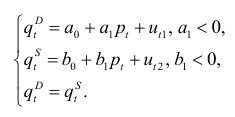
Построим приведенные уравнения, воспользовавшись условием равновесия (6.3):
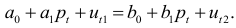
Последовательно разрешаем данное уравнение относительно 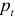 :
:
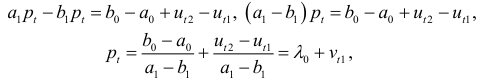
где 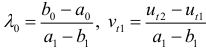 — случайный член. Подставив найденное значение
— случайный член. Подставив найденное значение 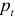 в одно из уравнений (6.1) или (6.2), найдем
в одно из уравнений (6.1) или (6.2), найдем 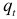 :
:
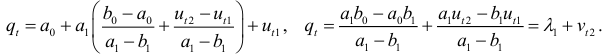
Система уравнений
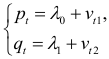
является приведенной. Применив МНК, найдем оценки параметров 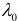 и
и 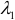 . Система (6.1) — (6.3) имеет четыре неизвестных параметра
. Система (6.1) — (6.3) имеет четыре неизвестных параметра 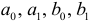 . Для определения неизвестных параметров
. Для определения неизвестных параметров 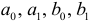 мы можем составить два уравнения
мы можем составить два уравнения 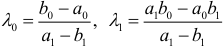 и, следовательно, мы не сможем однозначно определить параметры
и, следовательно, мы не сможем однозначно определить параметры 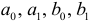 . Это означает неидентифицируемость исходной системы уравнений.
. Это означает неидентифицируемость исходной системы уравнений.
Рассмотрим эту же модель «спрос — предложение». Добавим в функцию спроса экзогенные переменные: 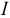 — доход потребителей и
— доход потребителей и 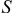 — объем сбережений, а в функцию предложения — цену
— объем сбережений, а в функцию предложения — цену 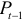 в предшествующий период. Получим модель с числом экзогенных переменных, превышающих количество структурных уравнений:
в предшествующий период. Получим модель с числом экзогенных переменных, превышающих количество структурных уравнений:
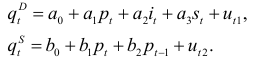
Воспользовавшись условием рыночного равновесия, можно преобразовать уравнения к системе приведенных уравнений
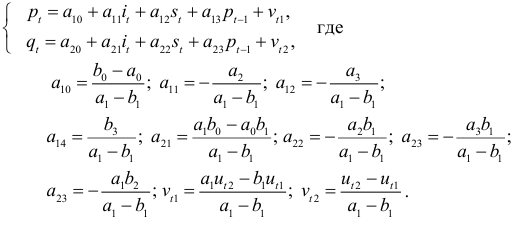
В системе (6.18), связывающей коэффициенты приведенных и структурных уравнений, восемь уравнений и семь коэффициентов
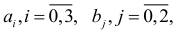
структурных уравнений. Поскольку соотношения (6.18) противоречивы, то однозначное определение структурных коэффициентов невозможно. В данном случае имеет место сверхидентифицируемость (переоопределенность).
Для определения идентифицируемости структурных уравнений применяются необходимые и достаточные условия. Прежде чем их сформулировать введем следующие обозначения:
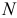 — число одновременных уравнений относительно
— число одновременных уравнений относительно 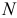 эндогенных переменных;
эндогенных переменных;
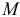 — число экзогенных или предопределенных переменных в системе;
— число экзогенных или предопределенных переменных в системе;
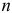 и
и 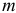 — количество эндогенных и экзогенных переменных в проверяемом на идентифицируемость уравнении;
— количество эндогенных и экзогенных переменных в проверяемом на идентифицируемость уравнении;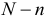 и
и 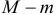 количество эндогенных и экзогенных переменных не входящих в проверяемое уравнение, но входящих в другие уравнения системы (исключенные переменные из данного уравнения).
количество эндогенных и экзогенных переменных не входящих в проверяемое уравнение, но входящих в другие уравнения системы (исключенные переменные из данного уравнения).
Первое необходимое условие. Уравнение идентифицируемо, если оно исключает, по крайней мере, 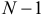 переменную (эндогенную или экзогенную), присутствующую в .модели: (N -/?) + (М — т )> N —
переменную (эндогенную или экзогенную), присутствующую в .модели: (N -/?) + (М — т )> N —
Второе необходимое условие. Уравнение идентифицируемо, если количество исключенных из уравнения экзогенных переменных не меньше количества эндогенных переменных в этом уравнении, уменьшенного на единицу:
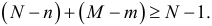
Знаки равенства в необходимых условиях соответствуют точной идетификации уравнения.
Необходимое и достаточное условия идентифицируемости. В модели, содержащей 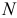 уравнений относительно
уравнений относительно 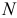 эндогенных переменных, условие идентифицируемости выполняется тогда и только тогда, когда ранг матрицы, составленной из исключенных из данных уравнений переменных, но входящих в другие уравнения системы, равен
эндогенных переменных, условие идентифицируемости выполняется тогда и только тогда, когда ранг матрицы, составленной из исключенных из данных уравнений переменных, но входящих в другие уравнения системы, равен 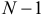 .
.
Рассмотрим применение данных условий для определения идентифицируемости структурных управлений.
В модели «спрос — предложение»
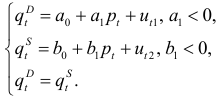
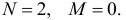
Для каждого из уравнений число эндогенных и экзогенных переменных равно:
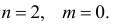
Так как
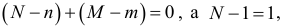
то не выполняется первое необходимое условие:
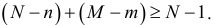
Следовательно, оба уравнения неидентифицируемы.
В модели
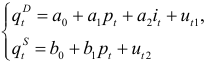
В функцию спроса добавлена экзогенная переменная 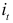 — доход потребителей, и в этой системе
— доход потребителей, и в этой системе
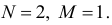
Для первого уравнения
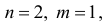
а для второго
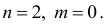
Тогда для первого уравнения
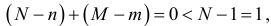
а для второго
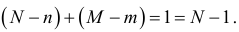
Это значит, что первое уравнение неидентифицируемо, а второе идентифицируемо. Следовательно, функция предложения определяется однозначно.
В модели
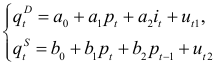
оба уравнения точно идентифицируемы, так как
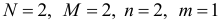
и выполняется необходимое условие
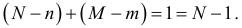
В модели
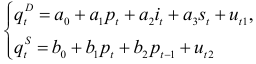
первое уравнение точно идентифицируемо, так как
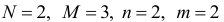
и выполняется равенство
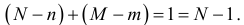
Второе уравнение является переопределенным, поскольку
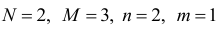
и
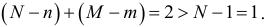
Оценим уравнения следующей структурной модели на идентифицируемость:
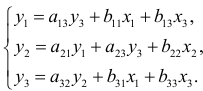
В данной модели три эндогенные переменные — 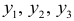 и три экзогенные переменные —
и три экзогенные переменные — 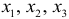 , т.е.
, т.е. 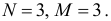 В первом уравнении
В первом уравнении 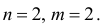 Тогда
Тогда
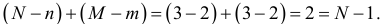
Следовательно, первое уравнение точно идентифицируемо. Построим матрицу из коэффициентов при переменных 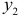 и
и 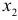 , отсутствующих в данном уравнении:
, отсутствующих в данном уравнении:
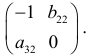
Ранг этой матрицы равен 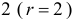 , следовательно, выполняется достаточное условие идентифицируемости. Подтверждается вывод сделанный по необходимому условию.
, следовательно, выполняется достаточное условие идентифицируемости. Подтверждается вывод сделанный по необходимому условию.
Для второго уравнения 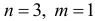 и выполняется равенство:
и выполняется равенство:
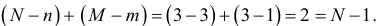
Данное уравнение также точно идентифицируемо. Проверим выполнимость достаточного условия. Для этого построим матрицу из коэффициентов при неизвестных 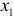 и
и 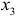 отсутствующих во втором уравнении:
отсутствующих во втором уравнении:
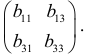
Ранг этой матрицы равен 2, следовательно, выполняется достаточное условие идентифицируемости, что подтверждает точную идентифицируемость уравнения.
Для третьего уравнения выполняется равенство
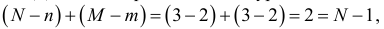
так как 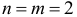 и ранг матрицы
и ранг матрицы
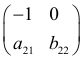
равен 2, что определяет точную идентифицируемость уравнения.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:

