Признаки существования пределов функции
Не всякая функция, даже ограниченная, имеет предел. Например, функция 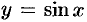 при
при 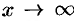 предела не имеет. Во многих вопросах анализа бывает достаточно только убедиться в существовании предела функции. В таких случаях пользуются признаками существования предела.
предела не имеет. Во многих вопросах анализа бывает достаточно только убедиться в существовании предела функции. В таких случаях пользуются признаками существования предела.
Теорема 17.10 (о пределе промежуточной функции). Если функция  заключена между двумя функциями
заключена между двумя функциями 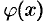 и
и 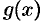 , стремящимися к одному и тому же пределу, то она также стремится к этому пределу, т. е. если
, стремящимися к одному и тому же пределу, то она также стремится к этому пределу, т. е. если
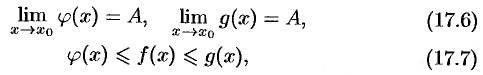
то
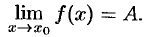
Из равенств (17.6) вытекает, что для любого 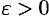 существуют две окрестности
существуют две окрестности 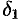 и
и 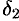 точки
точки  , в одной из которых выполняется неравенство
, в одной из которых выполняется неравенство 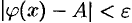 , т. е.
, т. е.

а в другой 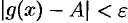 , т. е.
, т. е.

Пусть 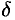 — меньшее из чисел
— меньшее из чисел 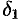 и
и 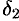 . Тогда в
. Тогда в 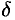 -окрестности точки
-окрестности точки  выполняются оба неравенства (17.8) и (17.9).
выполняются оба неравенства (17.8) и (17.9).
Из неравенств (17.7) находим, что
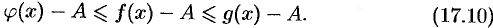
С учетом неравенств (17.8) и (17.9) из неравенства (17.10) следуют неравенства 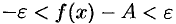 или
или 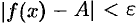 .
.
Мы доказали, что
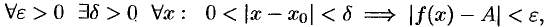
то есть 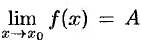 .
.
Теорему 17.10 иногда шутливо называют «принципом двух милиционеров». Роль «милиционеров» играют функции 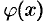 и
и 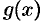 , функция
, функция  «следует за милиционерами».
«следует за милиционерами».
Теорема 17.11 (о пределе монотонной функции). Если функция  монотонна и ограничена при
монотонна и ограничена при 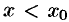 или при
или при 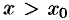 , то существует соответственно ее левый предел
, то существует соответственно ее левый предел 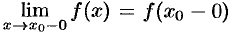 или ее правый предел
или ее правый предел 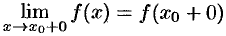 .
.
Доказательство этой теоремы не приводим.
Следствие 17.6. Ограниченная монотонная последовательность 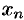 ,
, 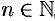 , имеет предел.
, имеет предел.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Бесконечно малые функции |
| Основные теоремы о пределах |
| Обратная функция |
| Сложная функция |

