Оглавление:
Необходимый признак сходимости как первый из специальных признаков, вообще говоря, не даст возможности судить о том, сходится данный ряд или нет. В этом мы убедились, рассматривая в лекции 32 ряд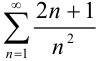 
(пример 32.6.). Необходимый признак для него выполняется, но исследование сходимости требует дополнительной проработки. В решении вопросов исследования сходимости данного ряда и других рядов хорошим аппаратом являются так называемые достаточные признаки сходимости. К ним относятся признаки сравнения, Даламбера, радикальный и интегральный Коши.
Рассмотрим их для положительных числовых рядов. Числовой ряд с неотрицательными членами называется положительным (знакоположительным). Заметим, что исследование сходимости отрицательных рядов (рядов с не положительными членами) осуществляется с помощью тех же достаточных признаков. Это связано с тем, что отрицательный ряд переходит в положительный путем умножения его на (-1), что в силу известного свойства (свойство 2 лекции 32), не влияет на сходимость ряда.
Признак сравнения позволяет исследовать положительный ряд на сходимость путем сравнения его с другим («эталонным») рядом, о котором известно, сходится он или нет.
Сформулируем признак без доказательства.
Признак сравнения: Пусть даны два положительных ряда 
и 
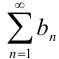. Если, начиная с некоторого номера, выполняется неравенство 
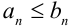, то
- из сходимости ряда 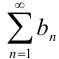следует сходимость ряда ;
- из расходимости ряда следует расходимость ряда .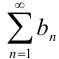
Другими словами,
- если общий член исследуемого ряда меньше общего члена сходящегося ряда, то исследуемый ряд сходится;
- если общий член исследуемого ряда больше общего члена расходящегося ряда, то исследуемый ряд расходится.
Обратимся к примерам использования признака сравнения для исследования сходимости положительных рядов.
Пример №33.1.
Исследуйте ряд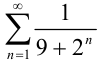 
на сходимость, применяя признак сравнения.
Решение:
Сравним данный ряд с рядом геометрической прогрессии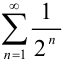 
, сходимость которого мы установили в примере 32.3. лекции 32. Имеем: 
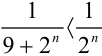. Таким образом, общий член нашего ряда меньше общего члена сходящегося ряда. Следовательно, по признаку сравнения, ряд 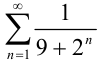сходится.
Ответ: 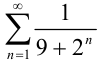сходится.
Пример №33.2.
Исследуйте ряд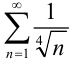 
на сходимость, применяя признак сравнения.
Решение:
Сравним данный ряд с гармоническим рядом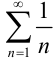 
, который расходится (лекция 32). Имеем: 
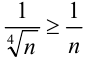. Таким образом, общий член нашего ряда больше общего члена расходящегося ряда. Следовательно, по признаку сравнения, ряд 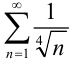расходится.
Ответ: 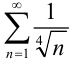расходится.
Признак сравнения позволяет исследовать сходимость положительных рядов, если удастся сравнить их с «эталонными» рядами, поведение которых в смысле сходимости известно.
В качестве «эталонных» обычно используют следующие ряды:
1. 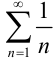— расходящийся гармонический ряд;
2. 
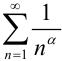, если 
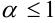— расходящийся обобщенный гармонический ряд,
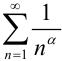, если 
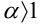— сходящийся обобщенный гармонический ряд;
3. 
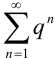, если 
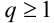— расходящийся ряд геометрической прогрессии,
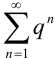, если 
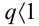— сходящийся ряд геометрической прогрессии.
Пример №33.3.
Исследуйте ряд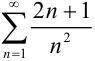 
на сходимость.
Решение:
Рассмотрим ряд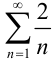 
. Поскольку он получается из расходящегося гармонического ряда 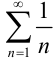умножением на 2, то, согласно свойству 2 числовых рядов (лекция 32), он расходится. Сравним исследуемый ряд с рядом 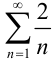. Имеем: 
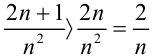, т.е. 
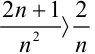. Таким образом, общий член исследуемого ряда больше общего члена расходящегося ряда. Следовательно, по признаку сравнения, ряд 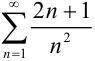расходится.
Ответ: 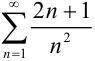расходится.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Свойства числовых рядов. |
| Необходимый признак сходимости ряда. |
| Признак Даламбсра. |
| Признак Коши (радикальный). |
