Оглавление:
Признак Даламбера
В отличие от признаков сравнения, где все зависит от догадки и запаса известных сходящихся и расходящихся рядов, признак Даламбера (1717-1783, французский математик) позволяет часто решить вопрос о сходимости ряда, проделав лишь некоторые операции над самим рядом.
Теорема 60.3. Пусть дан ряд (59.1) с положительными членами и существует конечный или бесконечный предел 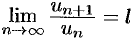 . Тогда ряд сходится при
. Тогда ряд сходится при 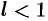 и расходится при
и расходится при 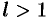 .
.
Так как 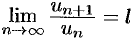 , то по определению предела для любого
, то по определению предела для любого 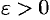 найдется натуральное число
найдется натуральное число 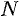 такое, что при
такое, что при 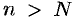 выполняется неравенство
выполняется неравенство
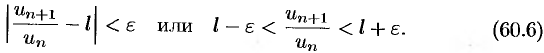
Пусть 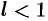 . Можно подобрать
. Можно подобрать 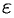 так, что число
так, что число 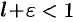 . Обозначим
. Обозначим 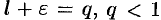 . Тогда из правой части неравенства (60.6) получаем
. Тогда из правой части неравенства (60.6) получаем 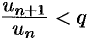 , или
, или 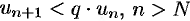 . В силу свойства 3 числовых рядов можно считать, что
. В силу свойства 3 числовых рядов можно считать, что 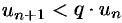 для всех
для всех 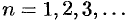 Давая номеру
Давая номеру 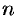 эти значения, получим серию неравенств:
эти значения, получим серию неравенств:
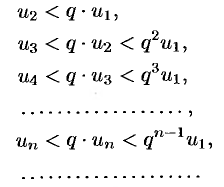
т. е. члены ряда 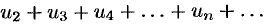 меньше соответствующих членов ряда
меньше соответствующих членов ряда 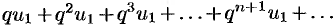 , который сходится как ряд геометрической прогрессии со знаменателем
, который сходится как ряд геометрической прогрессии со знаменателем 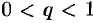 . Но тогда, на основании признака сравнения, сходится ряд
. Но тогда, на основании признака сравнения, сходится ряд  , следовательно, сходится и исходный ряд (59.1).
, следовательно, сходится и исходный ряд (59.1).
Пусть 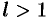 . В этом случае
. В этом случае 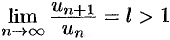 . Отсюда следует, что, начиная с некоторого номера
. Отсюда следует, что, начиная с некоторого номера 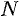 , выполняется неравенство
, выполняется неравенство 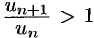 , или
, или 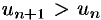 , т. е. члены ряда возрастают с увеличением номера
, т. е. члены ряда возрастают с увеличением номера 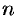 . Поэтому
. Поэтому 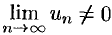 . На основании следствия из необходимого признака (см. п. 59.3) рад (59.1) расходится.
. На основании следствия из необходимого признака (см. п. 59.3) рад (59.1) расходится.
Замечания.
- Если
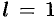 , то рад (59.1) может быть как сходящимся, так и расходящимся.
, то рад (59.1) может быть как сходящимся, так и расходящимся. - Признак Даламбера целесообразно применять, когда общий член ряда содержит выражение вида
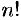 или
или 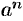 .
.
Пример №60.4.
Исследовать на сходимость ряд 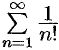 .
.
Решение:
Находим
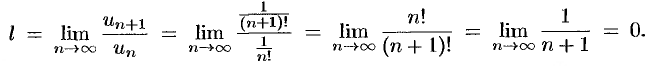
Так как 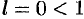 , то данный ряд по признаку Даламбера сходится.
, то данный ряд по признаку Даламбера сходится.
Дополнительный пример №60.5.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Необходимый признак сходимости числового ряда |
| Достаточные признаки сходимости знакопостоянных рядов |
| Радикальный признак Коши |
| Интегральный признак Коши |

