Признак Даламбера

В отличие от признака сравнения, где многое зависит от догадки и запаса “эталонных” рядов, признак Даламбера часто позволяет исследовать сходимость ряда, проделав лишь некоторые операции над ним. Сформулируем признак без доказательства.

Признак Даламбера: Пусть дан положительный числовой ряд , и существует конечный или бесконечный предел 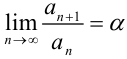. Тогда:

• если 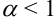, то ряд сходится;
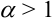• если , то ряд расходится;
• если 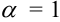, то признак не применяется (вопрос о сходимости ряда остается открытым).

Исследовать ряд на сходимость по признаку Даламбера удобно по следующему алгоритму:

1) найти ;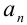

2) найти ;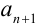

3) найти ;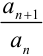

4) найти предел отношения на бесконечности 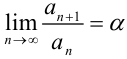и проанализировать полученное значение:

• если 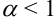, то ряд сходится;
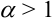• если , то ряд расходится;
• если 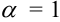, то признак Даламбсра ответа не дает (требуется дополнительное исследование).

Обратимся к примерам использования признака Даламбсра для исследования сходимости положительных рядов.

Пример №33.4.

Исследуйте ряд 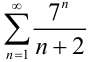на сходимость, применяя признак Даламбера.

Решение:

Для исследования сходимости ряда по признаку Даламбера воспользуемся алгоритмом:

1) найдём : ;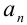

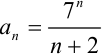2) найдём : ;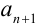

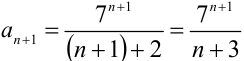3) найдём :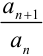

;

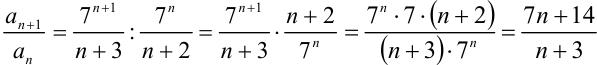4) найдём :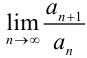

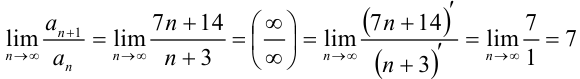(при раскрытии неопределенности 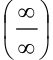использовали правило Лопиталя). Получили, что .

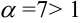Значит, по признаку Даламбера ряд 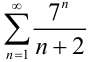расходится.

Ответ: 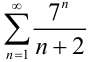расходится.

Пример №33.5.

Исследуйте ряд 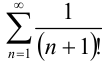на сходимость, применяя признак Даламбера.

Решение:

Для исследования сходимости ряда по признаку Даламбера воспользуемся алгоритмом:

1) найдём : ;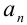

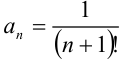2) найдём : ;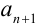

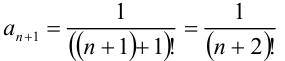3) найдём :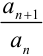

;

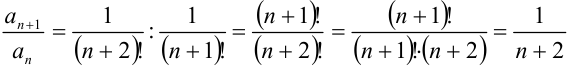4) найдём : .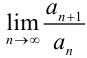

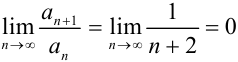Получили, что 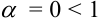. Значит, по признаку Даламбера ряд 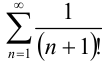сходится.

Ответ: 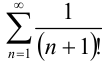сходится.

Заметим, что признак Даламбера целесообразно применять в том случае, когда общий член ряда содержит выражение вида 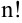или .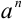

Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:

Предмет высшая математика

Другие лекции по высшей математике, возможно вам пригодятся:

Необходимый признак сходимости ряда.

Признак сравнения.

Признак Коши (радикальный).

Интегральный признак Коши.