Приведение системы сил, действующих на твердое тело, к динаме. Уравнения равновесия твердого тела
Пусть система сил, действующих на твердое тело, приведена к началу координат и пусть R — результирующая сила, а m — момент результирующей пары. Из теории скользящих векторов известно, что для такой системы сил всегда найдется такая точка 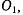 при приведении к которой момент результирующей пары
при приведении к которой момент результирующей пары 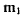 будет коллинеарен результирующему вектору силы (рис. 98). Новая пара имеет момент
будет коллинеарен результирующему вектору силы (рис. 98). Новая пара имеет момент
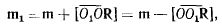
а условие коллинеарности векторов R и 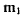 аналитически представится в виде равенства
аналитически представится в виде равенства
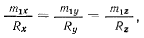
или после подстановки значений 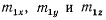 в виде
в виде
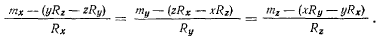
Последние уравнения определяют прямую линию, при приведении ко всем точкам которой момент результирующей пары будет коллинеарен результирующему вектору. Эта прямая называется динамой.
Когда на оси динамы момент результирующей пары равен нулю, система сил, действующих на твердое тело, становится эквивалентной одной результирующей силе, направленной вдоль оси динамы. Такая результирующая сила, эквивалентная всей системе сил, действующих на твердое тело, называется равно действу ющей силой системы. Очевидно, что необходимым условием существования равнодействующей силы будет равенство
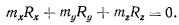
Могут представится следующие четыре различных случая приведения системы:
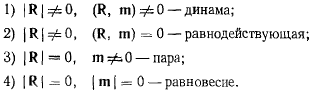
В последнем случае два векторных уравнения равновесия
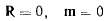
дают шесть скалярных уравнений в проекциях на декартовы оси координат
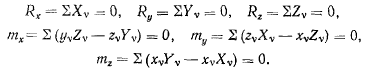
Уравнения будут иметь более или менее сложный вид в зависимости от выбора точки приведения системы сил и успех в решении задачи о равновесии до некоторой степени будет зависеть от выбора точки приведения системы сил.
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:
Предмет теоретическая механика
Эти страницы возможно вам будут полезны:
| Произвольная система сил, действующих на твердое тело |
| Условия равновесия системы сил, действующих на твердое тело |
| Условия равновесия системы твердых тел |
| Плоская система сил |

