Оглавление:



Приведение к двум векторам
- Система движущихся векторов может быть заменена 2 векторами бесчисленными способами, 1 из которых пройдет через любую точку. Во первых, система Pp P2…, Pn это 3 произвольно взятые точки O, а не Op O2 1 вектор на прямой линии рис. 17. Разложим вектор A1P1 на 3 составляющие вектора, ориентированные вдоль линий OAi и OXAi O2A1 соответственно. Затем переместите точку приложения каждого компонента вектора вдоль его линии действия, переместите первый компонент вектора в точку O, второй компонент в точку O1, а третий компонент в точку O2. Аналогично разложим вектор на 3 составляющие. Перенесите вектор x, направленный вдоль прямой OA2, OGA2, O2L2 в точку O, Op O2 и т. д.
Вектор приложенный к точке o имеет вектор ПП результата, вектор приложен к точке ФП имеет Р2 результат, а вектор приложен к точке O2 имеет 3 результата. Итак, даны системы векторов, 3 произвольные точки o, эквивалентные системы векторов 3 в случае ОП О2 Заменено на 2×3. Вектор P oa1r O2 1 разложен на 3 вектора вдоль линии. Такое разложение возможно каждый раз. Если точка равна 3 точкам O, Op O2 не находится в plane. In в таких случаях эти линии образуют трехгранное тело. Если точка Ar находится в плоскости OGO2, но вектор Px в ней отсутствует, то точку приложения этого вектора можно переместить вдоль его линии действия так, чтобы она не находилась в указанной плоскости.
Чтобы такое определение имело смысл, необходимо показать, что значение момента не зависит от выбора точки на оси. Людмила Фирмаль
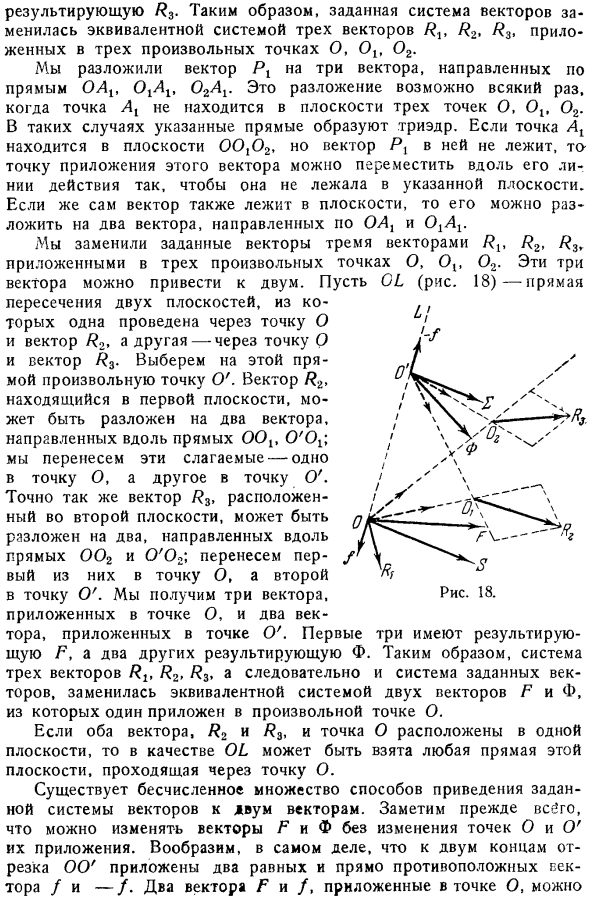
Если сам вектор также находится в плоскости, его можно разложить на 2 вектора, ориентированных вдоль OAG и O1A1. Я заменил данный вектор на 3 вектора fp P2, примененные к любым 3 точкам O, O , O2.Эти 3 вектора можно свести к 2. Прямая Обь рис. 18 2. пересечение двух плоскостей.1 плоскость проходит через точку O и вектор 2, а другая 1 плоскость проходит через точку O и вектор P3.Выберите любую точку O на этой линии. Вектор H2 в первой плоскости можно разложить на 2 вектора вдоль прямой OOR O X.
Передайте эти члены 1 в точку O, другой в точку O .Аналогично вектор P3, расположенный во 2 й плоскости, может быть разложен в 2 х направлениях вдоль линий OO2 и O O2.Перенесите первый из них в точку O, а второй в точку O .Получаем 3 вектора и 2 вектора приложенных к точке O Тор, приложенный в точке O. первые 3 Это P результата, другие 2 F результата. result. So, система из 3 векторов fp P2, P3, и поэтому система данного вектора заменяется эквивалентной системой из 2 векторов P и, 1 из которых применяется к любой точке O. Если оба вектора P2 и P3, а также Точка O находятся в одной плоскости, то любая линия этой плоскости, проходящая через точку O, может считаться OB.
- Существует бесчисленное множество способов свести систему данного вектора к 2 векторам. Во первых, обратите внимание, что вы можете изменить вектор P и Phi без изменения точек O и O в вашем application. Таким образом, фокус плоскости, проходящей через вектор P или, находится в другом векторе, и эти векторы находятся в 2 сопряженных линиях O и D.
Фактически, представьте, что 2 равных противоположных вектора и применяются к 2 ребрам сегмента OO .2 вектора P и, примененные в точке O, являются исходными системами основного вектора и основными системами 2 векторов в тех же точках рис.19.Если вы берете что то в векторной линии P Добавьте 1 вектор 5 и 2 вектора Phi , примененные точкой O к 1 вектору 2.Таким образом, система из 2 векторов P и Phi заменяется системой эквивалентности 2 векторов 5 и E. плоскость в плоскости, проходящей через точку O и вектор F. точка приложения вектора 5 O является необязательной.
Момент не изменяется, когда вектор Рг перемещается вдоль своей линии действия, или когда точка В перемещается вдоль прямой, параллельной этому вектору. Людмила Фирмаль
Так как модуль вектора O произволен, то точку O можно перемещать по прямой O e любым способом, а следовательно, и по всей плоскости OO F. В общем случае 2 вектора P и Phi, соответствующие всем заданным векторам, не находятся в одной плоскости. Главный вектор и главный момент относительно произвольной точки равны на данный момент, например, вектор АП точки, то есть точки А, получается путем добавления геометрически равных вектора АП и вектора F к геометрически равных вектора ад на вектор АП. Главным моментом в точке А является момент вектора, поскольку момент вектора P равен нулю. Вектор AO будет перпендикулярен плоскости AO F, и точка A будет его фокусом пункт 17.
Линия, которая пересекает векторы P и Phi одновременно, явно является линией нулевого момента. И наоборот, если линия нулевого момента пересекает линию действия вектора P, она также пересекает линию действия вектора на конечных или бесконечных расстояниях. Это связано с тем, что момент вектора P относительно этой линии равен нулю, поэтому момент вектора Phi относительно нее также равен нулю. В разделе упражнений указано, что векторная система всегда может быть сведена к 2 таким векторам.
Смотрите также:
Предмет теоретическая механика
| Определение эквивалентности | Геометрическое истолкование инварианта |
| Элементарные операции | Приведение двух эквивалентных систем друг к другу |

