Оглавление:





Приведение двойного интеграла к повторному в случае криволинейной области.
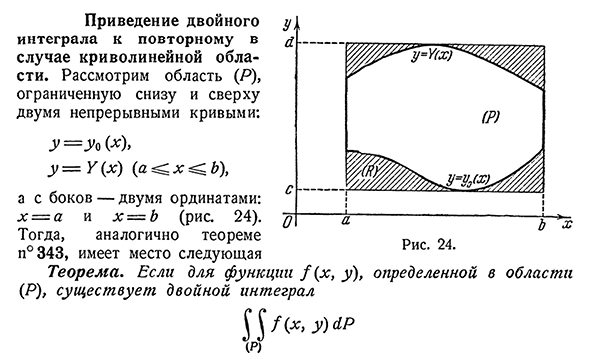
- В случае области кривой, чтобы повторить двойное интегрирование. Y=y (x), y=Y (x) (a^x^B\a двумя ориентациями в поперечном направлении: x=a и x=B (рис. 24). Тогда, подобно теореме n°343, возникают следующие теоремы. Если существует двойной Интеграл для функции/(x, y), определенной в области (P)) /(х,г)р Ага. Рис 24.252 глава XX1-двойной Интеграл[344 А для каждого постоянного значения x из[a, B] — простой Интеграл Г(H) Я(Х)=§/(Х,у)Лу, В примерно *)( *) Его значение на границе этой области не играет роли(см. n°341, G). Тогда
есть и повторный Интеграл В7{х) §/(х,г)С1, И о том, что )( И справедливость уравнения B(х) У/(Х,у)Лу. (6) U вых и) Это доказательство основано на сведении этого случая к тому, который учитывается в n°343. Чтобы быть точным, вы можете использовать область (P) как прямоугольник(/?)=[А,B;С,], /(икс., год|=) Предполагая, что C=PIP_u0 (x), tah U (x) (рис. 24), и определение а^х^г^х^г В этом прямоугольнике функция/(x, y) будет выглядеть так:/(x, y),
если точка (x, y) принадлежит области (P), то O в другой точке (P) прямоугольника. Указывает, что эта функция удовлетворяет Людмила Фирмаль
условию теоремы n°343. Прежде всего, она интегрируема в области (P), где она совпадает с условной интегрируемой функцией/(x, y). /(х, г) (1П=г г / {х, у)<1Р. (Р)(Р)) С другой стороны,/(x, y)=0 находится вне (P) и, следовательно, может быть интегрируемо с остальной частью прямоугольника (<2)=(P)—(P))、 / * (х,г)СШ=0. «?») 344]§2. Вычисление двойного интеграла 253 Тогда, благодаря n°341,2°, функция/является интегрируемым прямоугольником(C)、 С(/(х, Г) Л С — §§/(х,г)^р. (Я) (П) В общем (7) Постоянное значение X на [А,B]является неотъемлемой
У0(х)г(х)г)Лу — §/<1У+г/<г+г/ * (1У, S U o (X)U (x) Для каждого из трех интегралов это правильно. Фактически, интервал[C, y(x) и(K(x), C1]изменяет функцию y/(x,_u)=0, так что первый и последний Интеграл существуют и равны нулю. Второй Интеграл совпадает с Интегралом функции/(x, y): Г (х) г(х} Г г(х, г) г г=г/{х,г)г, УО (х) так как/(x,y)=/(x, y) [_u0 (x), Y (x)] для y. наконец, Y (x)^ / (x,y)<1U=y/(x, y) O y. (8) 3 ‘ 0(X) Благодаря вышеприведенной теореме функция/также имеет
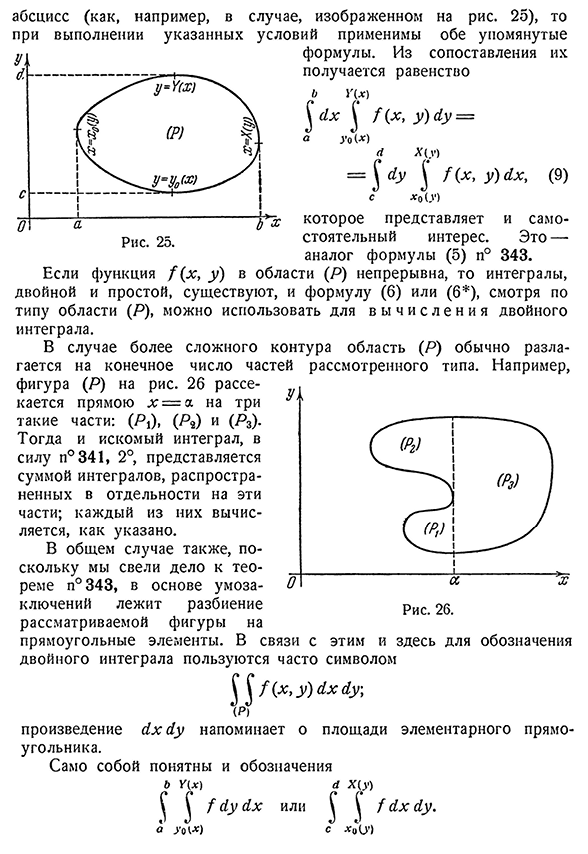
- повторяющийся Интеграл, равный двойному [n°343, (4)см.]: b A{x,.х) ар=у U(х, у) АУ. (Я)С Между тем, (7) и(8). как правило, мы видим, что это выражение эквивалентно выражению(6). Если область (P) является трапецией другого типа кривой, а кривая x=x0 (y), x=X (y) (C^y^C1) и прямая Y=C, Y=C1, то вместо (6) выражение a x (y)/(x, y) заключено в виде трапеции.)) (П)с х0(г)) В предположении, что существует более простое интегрирование, чем x, наряду с двойным интегралом _u=SOP$1. Z если контур (P) области Амазонки пересекается только в двух точках, то вертикальная ось параллельна прямой и osi254 глава XXI. обе параллельные линии двойного
интеграла[344 Для риса. 25), а затем оба упомянули свои сравнения Горизонтальной оси(например, как и в случае, когда выполняются вышеуказанные условия, применяется формула. Равенство Что?(икс) У (1х/(х, 3) Лу= А у О (х) (Я Х (В) =Лу/(х,г)ЛК,(9) В X$(в) Это независимая забота. Это аналог формулы (5) n°343. Функции в области/(x, y) (P) непрерывны, интегральны, есть простые, формула (6) или (6) является V y h и s l e n и I, в зависимости от случая типа
двойной области (P). Для более сложных контуров область (P) обычно разлагается на конечное число частей рассматриваемого типа. Людмила Фирмаль
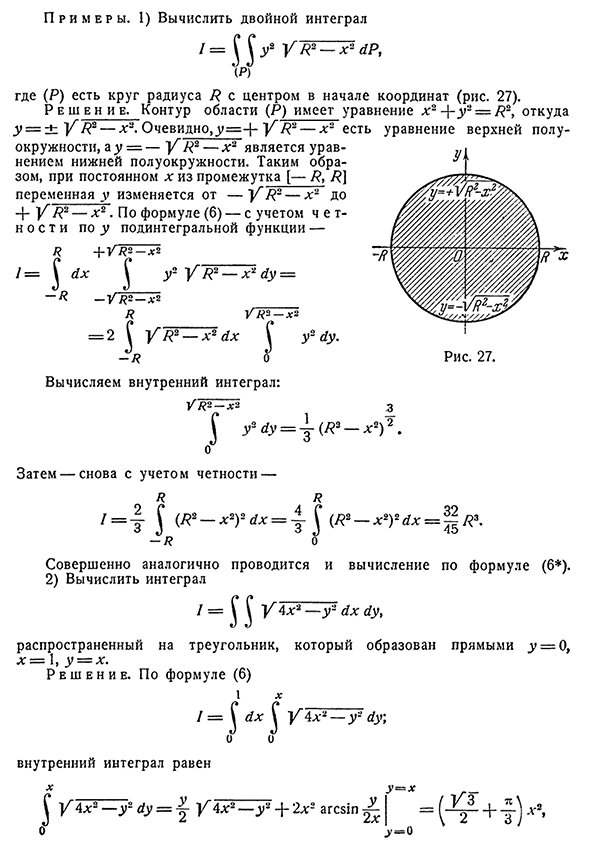
Например, он показывает рисунок (P). 26 рассекается на три такие части прямолинейно x=a: (RD (P2) и (P3). В свою очередь, искомый Интеграл представляется суммой интегралов, которые раздельно распределены в этих частях, для n°341,2°. Даже в общем случае, сведя дело к теореме № 343, в основе вывода лежит деление рассматриваемой фигуры на четырехугольные элементы. В связи с этим и для обозначения двойного интеграла здесь часто используется знак (Y/(X’y) Ah4U) ; (П) произведение y Hyu напоминает площадь основного прямоугольника. Самоочевидны и символы Б г(х) /Ю-ых И сердце тоже ) х(г} Или U/YH Yu. С x^y}344]§2. Вычисление двойного интеграла 255 P Lee MA 1) вычислить двойной Интеграл Где (P) — окружность радиуса#, центрированная в начале координат(рис. 27). Контур области (P) вычисляется по уравнению x2 — [- Y2 — # 2,y=±yg^2-x2. Очевидно, что^= — / — Y2-x2 имеет верхнюю половину
уравнения, а y= — Y P2-x2 является нижней половиной уравнения. Таким образом, в константе x из интервала[—P, P] переменная y изменяется от-Y P2-x2 до+Y P2-x2. В соответствии с формулой, принимать во внимание (6)-ч ет Н О С Т и г subintegral функции — Вычислить внутренний Интеграл: Затем снова примите во внимание паритет — Я Я Я Я Я / =4Г(2-* 2)2^= 4У(У2 — * Т^==|яз- — / ? расчет по формуле o (6) осуществляется совершенно аналогично. 2) вычислить Интеграл Я Х2-У2 yx4u, Прямая линия Y=09p вытянулась в треугольник, образованный esh. По формуле(6) 1X Я=§ух u4x2-группы U2 и U\и о Внутренний Интеграл равенY=~ ~ XX Y4x2-y2=Y4x2-Y+2L2ags81p^ / = O
u=0256 глава XXI. двойной Интеграл (344 И напоследок (, 6 но в этом случае мы столкнемся с Б О Л е е т р у д н ы К В а д р а т р ы. в таких случаях, когда вы выбираете путь, вычислите его. *) Этот предел здесь установлен только для того, чтобы избежать инвертирования подфункций до бесконечности;4) ниже он будет слабее. 3) вычислить Интеграл Л в, Y в В предположении, что p1,<7 1*). Мы имеем формулу (5) 1\ — x1 Наконец-то!: G (R)) l ‘ ^0, y>0x+Y1 это выражение принадлежит Дирихле. 4) p<1 (или (?< 1) функция парциальной плотности бесконечна при x=0 и 0<^^1 (или y=0 и 00): — Икс Икс?-1(1 х 1 ты-1 Ты== Е Первый Е Если сейчас вам прямой е 0 (выжать заштрихованная полоса на рис. 28, когда мы отделили»специальную»
строку, было бы-в (p, # 4-1) тоже на пределе. Это ограничение является неправильным интегралом цели. В общем случае, когда функция парциальной плотности становится бесконечной вдоль отдельной («специальной») точки или некоторой («специальной») линии, они выделяются определенной областью (345]§2) и вычисляются для двойного интеграла 257. Например, вычислите интегралы внешних областей этих соседей, сожмите их соседей в точки, сожмите b, если есть предел, и дайте несоответствующие интегралы. Аналогично мы строим понятие «неправильных» интегралов, распространяющихся на бесконечные области. В случае положительных функций парциальной плотности выбор»специальной» точки и окрестности редукции линии или расширяющейся граничной области не имеет значения.
Смотрите также:
Решение задач по математическому анализу
| Интеграл как аддитивная функция области; дифференцирование по области. | Механические приложения |
| Приведение двойного интеграла к повторному в случае прямоугольной области | Вывод формулы Грина |

