Оглавление:


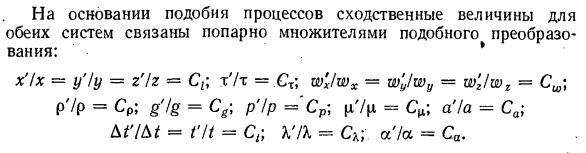







Приведение дифференциальных уравнений конвективного теплообмена и условий однозначности к безразмерному виду
- Редукция дифференциальных уравнений конвекции Передача тепла к безразмерным формам и ясным условиям Чтобы применить на практике теорию подобия в случае конвективного теплообмена, описываемого системой дифференциальных уравнений и условиями единственности с большим числом переменных, необходимо сначала узнать число подобия, содержащееся в уравнении подобия. , Эти
системы дифференциальных уравнений, включая дифференциальные уравнения теплопередачи между твердыми телами в движущейся жидкости и внешней средой V, энергии или теплопроводности, движения вязких несжимаемых жидкостей (или уравнений Навье-Стокса) и непрерывности Числа, раскрывающие структуру. Хотя показанная система уравнений обеспечивает полное
математическое описание явления теплопередачи с условием единственности r, сталкивается с большими трудностями. Поскольку физические величины измерения могут быть связаны с безразмерными I-комплексами, число комплексов меньше, чем количество величин,
аналитическое решение этой системы Людмила Фирмаль
составляющих эти комплексы. Это значительно упрощает исследование физических процессов. Полученный безразмерный комплекс можно рассматривать как новую переменную c. Поэтому для получения числа сходств используется следующая формула: Уравнение движения вязкой жидкости Навье-Стокса (Dwx. „Dwx. Dwx. Dwx \ + w ‘- * r + 94rr f a * r v dx * n do * ^ dz * g ‘ (Для сокращения
вычислений уравнение Навье-Стокса дано только для осей ); Уравнение неразрывности жидкости _ | —_ Q •. (2b.13) И дг Уравнение энергии жидкости dt, а /. /. дт / дх, д4. дх \ / ог … Уравнение теплопередачи на границе между окружающей средой и твердым телом aAt- — X (dt / dx) CT. , (26-15) Напишите уравнения для двух похожих систем. «Процесс, который происходит в первой системе, описывается уравнениями (26-12) — (26-15). Процесс, который
происходит во второй системе, описывается тем же уравнением, что и процесс в первой системе. Но похожие значения имеют индекс (‘). / dsh’kh ;, dw’x, dwx \ дх \ дх’2 до’2 дз’1) dw ‘dw’ dw ‘ a / ‘,: / dt’, / dt ‘,, dt’ (a2 / ‘. dCh’.dCh’ от , / Dt, dt ‘, dt’ (a2 / ‘, dc’, dc ‘\ /P|L.oh ‘At’ = -X ‘(dt’ / dx ‘) CT (26-19) Исходя из сходства процессов, одинаковые значения в обеих системах попарно связаны одинаковыми коэффициентами преобразования. x’lx = yChu = rChr = C {\ m7m = Cx \ w’x / wx = w’y / wy = w’z / wz = Сш \ р ‘/ р =
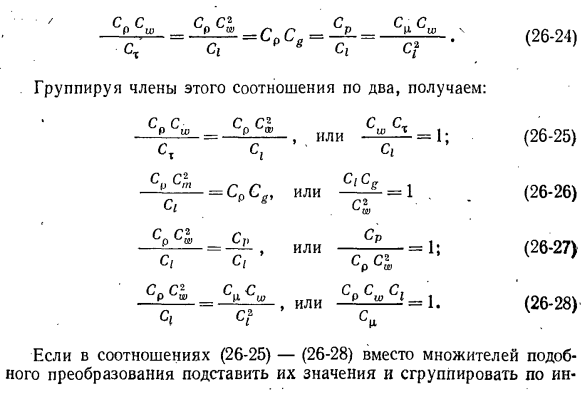
- Ср; g’lg = Cg-p’ / p = Сp] = C ^; a ‘/ a = Ca; M’lM = t’lt = Ct \ VA = Cx; ct’ / a = Ca. Выразите все переменные в уравнении (26-10) — (26-19) секунд • Система с коэффициентами пересчета, аналогичными первым системным переменным: CP Cu> l ^ x. CP C%> л /. , Dw St dt C / \ x dx y du 1 dg P * | C / ^ V ^ С? «Гr-Cr> -C’L ^ Группировка терминов в этих отношениях на две части: = Или кт с, с, = 1; = 1. C? P-g g или c, см cg Ci Ci C; или вода s, «C / ‘ср. C» CQ Cw или CP N Ci s? «» В соотношениях (26-25) — (26-28) вместо таких коэффициентов преобразования
сгруппируйте эти значения по индексу, чтобы получить следующий номер сходства. Но — то же самое; • (26-29) Fr = то же самое; (26-30) w2 ‘4 * и = — £ — = — ^ — = то же самое; (26-31). Low rou2 Re — ^ — = — ^ = То же самое, (26-32) V. v Где Ho — число гидродинамических синхроний и характеризует скорость изменения поля скоростей движущейся жидкости. Fr — число Фруда, которое определяет отношение инерции к гравитации. Она является числом Эйлера, которое характеризует
отношение силы давления к силе инерции. Re — число Рейнольдса. Это отношение силы инерции к силе вязкости и определяет характер потока жидкости. сходства двух или более систем. Для похожих точек они имеют одинаковое значение. Из уравнений энергии (26-14) и (26-22) мы имеем следующее соотношение: Или • (26-33) ct cf c? • CULCL = C ± CL) или С * СГ = к (2б.34) Cl Cl Ca Подстановка
Числа подобия Ho, Fr, Eu и Re используются для изучения гидродинамического Людмила Фирмаль
этих значений вместо аналогичных коэффициентов преобразования и деление переменной дает следующий номер подобия: То же, что и выше ;-( 26-35) rol- * , Pe = —- идем, • (26-36) Но где Fo — это число Фурье, мера тепловой одновременности, которая характеризует взаимосвязь между скоростью изменения температурного поля, физическими параметрами и размером тела. Re — число Пекле, число подобия
конвективного теплообмена. Подставляя значение, равное -A / sr, в число Fe вместо коэффициента термодиффузии a и умножая числитель и знаменатель на избыточную температуру ft, Pe = т.е. ■ (л / *) * Число подобия характеризует тепло, передаваемое конвекцией, а знаменатель характеризует тепло, передаваемое теплопроводностью. Из уравнений теплопередачи (26-15) и (26-23) получается следующее соотношение: _ _ C, C, C s, ct = или -4- ^ = 1. , (26-37) H ck После
преобразования и разделения переменных, Nu = — = то же самое, — (26-38) Nu — это число Нуссельта, которое характеризует конвективный теплообмен между жидкой и твердой поверхностями. Число Нуссельта определяется тем же значением, что и число Био, но число Nu содержит теплопроводность теплоносителя, а число Bi содержит теплопроводность твердого тела. Числа Fo, Pe и Nu используются для определения термического сходства двух или более систем. Для похожих точек они имеют одинаковое значение. Разделив число Pe
на число Re, получим новое число Pr. Pr = Pe / Re = v / a, (26-39) Где Pr — число Прандтля, определяющее физические свойства жидкости. Число Pe может быть выражено как произведение чисел Re и Pr: Pe = Re. Pr = (wl / ) (v / a) = wl / a. (26-40) При изучении теплообмена в свободном потоке жидкости учитывается число Фруда, но значение скорости w, которое очень трудно измерить, должно быть исключено. Для этого умножьте Fr на Re2. Ga = Fr • Re2 = идерри, (26-41) Где -Ga — число Галилея, которое характеризует отношение силы тяжести к
молекулярному трению. • Умножьте полученное число Ga на симплекс (p-p0) / po. Где p и p0 ‘- плотность жидкости в двух точках и получают новое число. A L AR • & 1 * DR. / ОС ЛОХ Ar является архимедовым числом, определяющим условия свободного движения среды. Симплекс (p-Po) / p <> заменяется на {W, если плотность жидкости изменяется из-за разницы в температуре в различных точках [p = p0 x X (1-PAO). Где (3 — коэффициент объемного
расширения) среды (когда газ р = 1/7). В этом случае номер Архимеда меняется на новый номер. Cr = L ^, (26-43) Здесь Gr — число Грасгофа, которое характеризует отношение подъемной силы, вызванной разницей между плотностью жидкости и силой молекулярного трения. Числа подобия Fr, Ga, Ar и Gr идентичны. Это те же четыре типа.
Смотрите также:
Решение задач по термодинамике
| Числа подобия | Уравнения подобия |
| Теоремы подобия | Средняя температура. Определяющая температура. Эквивалентный диаметр |

