Оглавление:




Принятие решений домашними хозяйствами
- Принятие решений на дому Как таковой, он объяснил потенциал домохозяйств в области потребления, но не объяснил, как выбрать все возможные варианты. Давайте перейдем к процессу принятия решений. Предположим, что домохозяйства в каждом периоде получают выгоду от потребления, и что уровень полезности, достигнутый с помощью комбинации C и C2, описывается функцией полезности UL = (I. (C ,, C2).
- Выберите комбинацию (C и C2 дают максимальное значение функции полезности, если C и C ^ соответствуют бюджетным ограничениям). Функция полезности UL (C {y C ^) работает как любая другая функция полезности, известная нам из теории потребительского выбора. Например, UL (Cr C ^ увеличивается как с C, так и с C2. Чем больше C или C2, тем лучше для дома.
Как и другие вспомогательные функции, самый простой способ представить свойства этой функции. Людмила Фирмаль
Безразличие к домашним хозяйствам заключается в создании кривой Чтобы понять, почему пересечение 6 бюджетных линий и оси X указывает уровень благосостояния дома, обратите внимание, что сегмент ОW состоит из двух частей: 0W, -0Q, ♦ + длина QxWi Равно 00, длина, равная W {<2 / (1 + r). Для более полного объяснения 7 кривых безразличия и их использования в теории потребления см .
Paul Samuebon & William Nordhaus, Economics (New York: McGraw-Hill. 1989). Рис. 4-3 Семейство неизбирательных кривых Выводит указанный уровень полезности UL0. На этом рисунке показано множество точек ULQ = / / (C ,, C ^), образующих отрицательный наклон и выпуклое выпуклое безразличие UL0. Важно понимать интерпретацию формы кривой безразличия.
Предположим, что вы находитесь в точке A (JL§-UL (C \, C ‘}). Что происходит, когда домохозяйство теряет часть C и получает количество C ^, которое не меняет полезность UL0? В результате значение C меньше, и C2 может переместиться в точку B, которая больше, чем A. Неизбирательная кривая имеет отрицательный наклон, что означает, что домохозяйство потеряно.
Получать больше C ^, чтобы благосостояние не ухудшалось, когда определенное количество C Выпуклость разнородной кривой отражает тот факт, что значение, которое необходимо увеличить для C2, чтобы компенсировать снижение C, зависит от исходного соотношения C и C2.
В точке A наклон кривой безразличия измеряет сумму, которая должна быть увеличена C2, чтобы компенсировать небольшую потерю C в домашнем хозяйстве (отношение- (ДС2) / (ЛС,) является предельным коэффициентом замещения и (Ранее наше основное предположение состояло в том, что предельная норма замещения уменьшается, то есть абсолютное значение наклона кривой безразличия уменьшается по мере ее движения вправо вдоль нее.
Так как же действуют домохозяйства? Если вы планируете сократить потребление в текущем периоде и увеличить потребление в будущем, это соответствует точке B на диаграмме. 4-3, будущее потребление должно значительно увеличиться, чтобы компенсировать незначительное снижение текущего потребления. Текущее потребление С уже очень низкое, поэтому домохозяйства не склонны его дополнительно сокращать.
Однако в точке C домохозяйство уже перенесло большую часть своего потребления, оставив очень мало на будущее. В этом случае домохозяйства с большей вероятностью жертвуют своей текущей единицей потребления за счет небольшого увеличения будущего потребления.
так Поэтому, когда предельная норма замещения уменьшается, описанная на фигуре неразборчивая кривая имеет выпуклость вниз. 4-3. Ограничение бюджета фигуры 4-3 определено для семейства разнородных кривых. Обратите внимание, что переход от одной кривой безразличия к другой кривой безразличия в направлении, указанном стрелкой, увеличивает уровень полезности домохозяйства.
- Домашние хозяйства максимизируют свои функции полезности, так что потребление находится на «самой высокой» кривой безразличия в отношении бюджетных ограничений. Как показано на рисунке. В 4-3 решение определяется кривой безразличия, связанной с ограничением бюджета точки А.
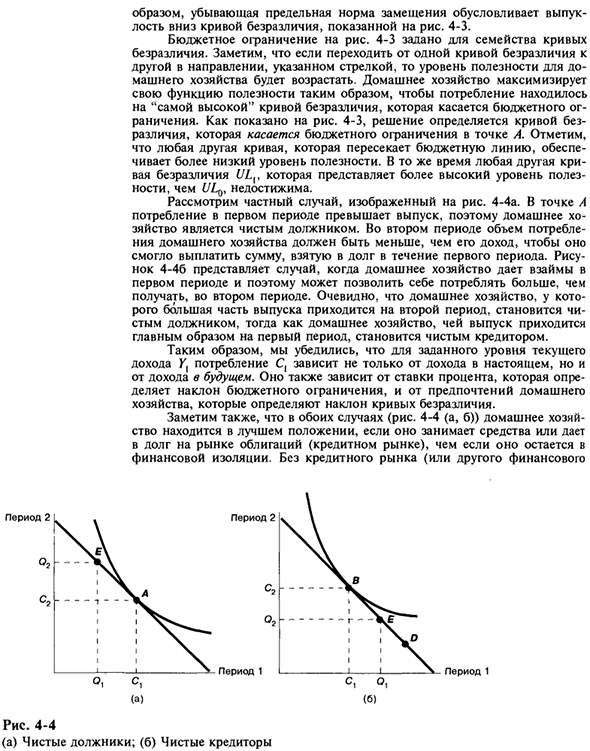
В то же время, другие кривые безразличия ULr, которые представляют более высокий уровень полезности, чем не могут быть достигнуты. Рассмотрим особый случай, показанный на рисунке. 4-4a. В точке L домашнее хозяйство является чистым должником, поскольку потребление в первом периоде превышает объем производства.
Обратите внимание, что другие кривые по бюджетной линии менее полезны. Людмила Фирмаль
Во втором периоде потребление домохозяйства должно быть меньше дохода, чтобы домохозяйство могло выплатить сумму, заимствованную в первом периоде. На рис. 4-46 показан случай, когда домохозяйства сдаются в аренду в первом периоде и могут потреблять больше, чем они получили во втором периоде.
Очевидно, что домашние хозяйства, на которые приходится большая часть производства во втором периоде, становятся чистыми должниками, в то время как домашние хозяйства, которые производят продукцию в первом периоде, становятся чистыми кредиторами. Поэтому при определенном уровне текущего дохода K мы убедились, что потребление C зависит не только от текущего дохода, но и от будущего дохода.
Это также зависит от процентных ставок, которые определяют наклон бюджетных ограничений и предпочтений домохозяйств, которые определяют наклон кривой рецессии. В обоих случаях (Рисунки 4-4 (a, b)) домохозяйства имеют больше возможностей брать или одалживать деньги на рынке облигаций (кредитном рынке), чем если бы они оставались финансово изолированными.
Пожалуйста, обратите внимание, что. Кредитный рынок (или другие финансы) Рис. 4-4 (A) Чистый должник; (b) Чистый кредитор На рынке возможны кредиты и займы) домашние хозяйства вынуждены потреблять весь свой продукт каждый период. Найдя кривую безразличия через начальную точку распределения средств, вы можете определить уровень полезности, которого достигнет изолированное домашнее хозяйство.
На обоих рисунках кривая безразличия представляет самый низкий уровень полезности по сравнению с тем, что может быть достигнуто, когда домашние хозяйства превращаются в рынок облигаций (кредитный рынок). Таким образом, использование ценных бумаг улучшает благосостояние домохозяйств, поскольку позволяет со временем перераспределять потребление. Это основные моменты, которые необходимо развить в оставшейся части этой главы.
Смотрите также:
| Домашнее хозяйство — основная ячейка экономики | Теория потребления с постоянным доходом |
| Динамическое (многопериодное) бюджетное ограничение | Модель жизненного цикла потребления и сбережений |
Если вам потребуется помощь по макроэкономике вы всегда можете написать мне в whatsapp.

