Принцип возможных перемещения

Принцип возможных перемещения

Определения. Будем рассматривать систему материальных точек 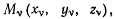на которые действуют некоторые заданные активные силы 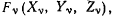предполагая, что на точ-

ки системы наложены связи, не изменяющиеся со временем и ограничивающие перемещения точек системы. Множество всех бесконечно малых перемещений точек, допускаемых наложенными на систему связями, называется возможными перемещениями системы.

Возможные перемещения могут быть как освобождающими, при которых некоторые из точек системы покидают наложенные на систему связи (освобождаются), так и неосвобождающими, при которых наложенные на систему связи сохраняются и после перемещения системы. Так, например, материальная точка М, подвешенная при помощи нерастяжимой гибкой нити к неподвижной точке 0 (рис. 121), может находиться в равновесии под действием некоторых сил, если расстояние точки от центра не превышает длины нити. Условие связи здесь может быть записано в виде неравенства (соединенного с равенством)

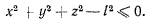
Тяжелый материальный шарик, находящийся на горизонтальном столе, может перемещаться по его поверхности или вверх, покидая стол. Выбирая систему координат так, чтобы оси хну были расположены в горизонтальной плоскости стола, а ось z была бы направлена вертикально вверх, условие связи запишем в виде

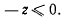
Если в рассматриваемом положении равновесия та или иная связь не действует на материальную точку и не стесняет ее перемещении, то говорят, что такая связь находится в ненатянутом положении.

Так, например, рассматривая равновесие тяжелого шарика, находящегося внутри цилиндрической трубы с горизонтальной осью, и предполагая, что, кроме того, перемещения шарика стеснены наклонной плоскостью (рис. 122), условия связи можно представить в виде

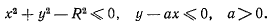
Вторая связь в положении равновесия не ограничивает возможные перемещения шарика и находится в ненатянутом состоянии.

Пели наложить на шарик связи вида

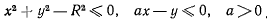
рис. 122), то в положении равновесия будут натянуты обе связи.

Ненатянутые связи не ограничивают возможные перемещения точек системы. Натянутые односторонние связи ограничивают возможные перемещения точек в одну сторону. Условия, накладываемые связями на возможные перемещения, получаются дифференцированием уравнений связи. Так, для рассмотренного выше случая (рис, 121) точки, подвешенной на нити, имеем условие связи в виде

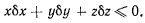
Здесь знак равенства имеет место лишь для перемещений по поверхности сферы радиуса R. Знак неравенства отвечает здесь перемещениям, ослабляющим натяжение нити. В случае натянутой нити на точку в положении равновесия будет действовать сила реакции со стороны нити — реакция натяжения. Она направлена в сторону освобождающих перемещений ортогонально к поверхности связи. Рассматривая в этом случае работу силы реакции на произвольном возможном перемещении, будем иметь

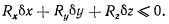
Работа будет равна нулю для всех возможных перемещений, при которых нить остается в натянутом состоянии (неосвобождаюшее перемещение), и будет положительной для перемещений, при которых нить ослабевает, т. е. связь переходит в не натянутое состояние.

Обозначим через 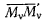вектор бесконечно малого перемещения точки 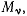возможного при наложенных на систему связях. Проекции этого вектора на оси координат обозначим через 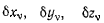и будем называть их вариациями координат. Заменив наложенные на точку 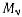связи силой реакции 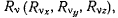действие которой эквивалентно действию связей, можно рассматривать систему, как освобожденную от связей, но находящуюся под действием активных сил 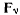и сил реакции 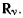Из всех связей, которые вообще могут быть наложены на систему материальных точек, будем рассматривать лишь такие, сумма работ реакций которых на любом возможном перемещении системы неотрицательна и, следовательно, удовлетворяет условию

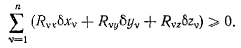
Связи, удовлетворяющие этому условию, будем называть идеальными. Знак равенства здесь соответствует неосвобождаюшим перемещениям. Освобождающим возможным перемещениям соответствует знак неравенства, если только соответствующие силы реакции отличны от нуля.

Примером идеальных связей являются гладкие связи, не препятствующие перемещениям материальных точек вдоль поверхностей связи. Силы реакции таких связей всегда ортогональны к неосвобождающим перемещениям точек системы и направлены в сторону освобождающих возможных перемещений, поэтому условие идеальности оказывается выполненным. Идеальными могут оказаться и негладкие связи. Покажем это на примере.

Пример:

Исследовать состояние равновесия тяжелого колеса, находящегося на шероховатом горизонтальном рельсе

Решение:

Предположим, что на колесо действуют две горизонтальные силы 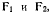как это указано на рис. 123. Тогда уравнения равновесия получат вид

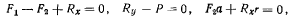
откуда сразу следует, что колесо будет находиться в равновесии, если выполняется условие

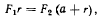
то тогда горизонтальная составляющая силы реакции в точке касания будет равна

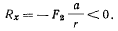
Таким образом, равновесие оказывается возможным лишь при шероховатых негладких связях. Связь эта является идеальной, так как работа силы реакции на возможном перемещении (вращении вокруг мгновенного центра скоростей) равна нулю.

Предполагая, что на систему материальных точек 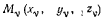действуют активные силы 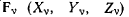я наложены односторонние связи вида

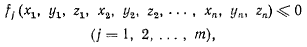
заметим, что если в положении равновесия связь удовлетворяется в виде неравенства, то она будет удовлетворяться в виде неравенства и в некоторой достаточно малой окрестности положения равновесия. Такие связи являются несущественными в данном положении равновесия, поэтому могут быть исключены из рассмотрения. Б дальнейшем будем рассматривать лишь такие связи, которые в данном положении равновесия натянуты и, следовательно, записываются в виде равенств (знак неравенства тогда отвечает другим положениям системы, отличным от данного положения равновесия).

Предположим, что связи, наложенные на материальные точки системы, задаются независимой системой функций, так что в матрице Якоби

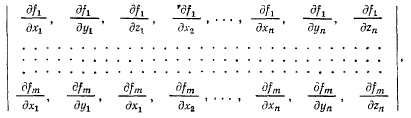
составленной из частных производных по всем координатам, оказывается отличным от нуля хотя бы один из миноров m-ного порядка. Тогда при натянутых связях положение системы определяется 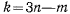независимыми параметрами.

При возможных перемещениях система может освобождаться от некоторых из связей, поэтому вариации координат при различных возможных перемещениях системы будут удовлетворять условиям

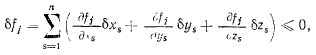
где знак равенства имеет место лишь для неосвобождающих возможных перемещений, а знак неравенства — для освобождающих. В силу независимости функций среди всех неосвобождающих перемещений будет только 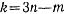независимых, а остальные будут выражаться через независимые. Наложенные на систему материальных точек связи могут быть заменены силами реакций 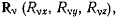действие которых эквивалентно действию связей.

Теорема Лагранжа о равновесии системы

Принцип возможных перемещений, предложенный Лагранжем, дает необходимые и достаточные условия равновесия системы материальных точек, стесненной идеальными связями, не зависящими явно от времени. Принцип этот заключается в том, что при равновесии системы материальных точек сумма работ всех сил, действующих на систему, на любом возможном перемещении неположительна и всегда равна нулю на всех неосвобождающих перемещениях системы. Впервые без доказательства принцип был сформулирован И. Вернулли в письме к Вариньону, который и поместил его в своей «Nouvelle Mecanique». Первое наглядное и достаточно общее доказательство, основанное на применении блоков, было предложено Лагранжем. Лагранж представил приложенные к системе силы в виде натяжений нитей, перекинутых через блоки и снабженных грузами. Приведем здесь другое аналитическое доказательство теоремы Лагранжа.

Лагранж рассматривал теорему только для случая двусторонних идеальных связей. Распространением теоремы на случай односторонних идеальных связен впервые занимался французский математик Ж. Фурье в связи с задачей о равновесии нити. В 1834 г. М. Г. Остроградским (1801 —1861) была предложена полная формулировка с доказательством обобщенной теоремы Лагранжа для случая односторонних связей.

Теорема Лагранжа. Для того чтобы система материальных точек, на которую наложены односторонние идеальные связи, не зависящие явно от времени, находилась в равновесии, необходимо и достаточно, чтобы в этом положении сумма работ всех активных сил, действующих на систему, на любом возможном перемещении системы была бы неположительной, т. е. удовлетворяла бы условию

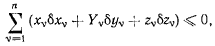
где знак неравенства отвечает освобождающим перемещениям, а знак равенства — неосвобождающим.

Доказательство. Необходимость. Пусть система материальных точек, на которую наложены освобождающие идеальные связи, находится в равновесии под действием активных сил с проекциями на неподвижные оси координат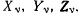

Тогда для каждой точки системы будут выполняться условия

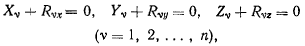
где 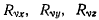— проекции сил реакций, действующих на v-тую точку системы. Определяя отсюда величины 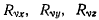и подставляя их значения в условие идеальности связей

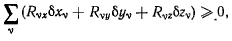
получим условие равновесия

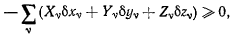
или

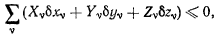
чем и доказывается необходимость.

Достаточность. Будем исходить от противного. Предположим, что при выполнении условия (а) система не находится в состоянии равновесия, т. е. в данном положении системы имеются неуравновешенные точки. Тогда, находясь первоначально в состоянии покои, неуравновешенная система начнет движение из этого состояния, подчиняясь наложенным на нее связям. Освободим теперь систему от связей, заменив действие последних действием сил реакций 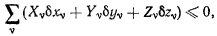— Подсчитаем работу всех сил на том перемещении, которое получает система, начиная движение из состояния покоя (в дальнейшем это перемещение будем называть действительным . Так как каждая точка системы начинает перемещаться из состояния покоя в направлении действия равнодействующей силы 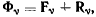действительные перемещения точек будут пропорциональны этим равнодействующим силам

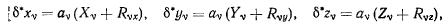
где 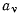— некоторые положительные числа. Действительное перемещение подчиняется наложенным на систему связям, т. е. является одним из возможных перемещений системы. Вычисляя работу всех сил, действующих на точки системы, на действительном перемещении будем иметь

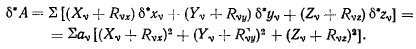
Заметим, что работа реакций связи на действительном перемещении системы всегда равна нулю, т. е.

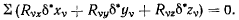
В самом деле, если действительное перемещение не является освобождающим, то, по определению, сумма работ реакций связи на этом перемещении равна нулю. Если же перемещение освобождающее, т. е. хотя бы одна точка системы 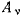под действием силы 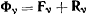покидает связь, то в рассматриваемом положении точка уже не оказывает действия на связь, и соответствующая сила реакции становится равной нулю. Тогда и работа этой силы реакции будет равна нулю на действительном перемещении. Итак, сумма работ реакций связи всегда равна нулю на действительном перемещении системы. Тогда из (b) и (с) сразу получаем

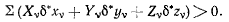
Предполагая, что при выполнении условия (а) система не находится в положении равновесия, мы обнаружили перемещение, на котором не выполняется условие (а), что противоречиво и, следовательно, система в действительности находится в равновесии.

Замечания. 1. В том случае, когда на систему материальных точек наложены только двусторонние связи, теорема Лагранжа получает более простую формулировку.

Теорема. Для того чтобы рассматриваемое положение системы было положением равновесия, необходимо и достаточно. чтобы в этом положении сумма работ всех активных сил на любом возможном перемещении системы равнялась нулю.

Доказательство этого предложения проводится так же, как и в общем случае. Условие же равновесия системы при двусторонних связях получает вид

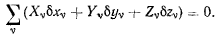
Это уравнение называется общим уравнением статики.

Уравнения равновесия системы

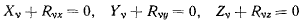
могут быть непосредственно получены из принципа Бернулли. В самом деле, рассматривая систему материальных точек 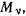на которую наложены идеальные связи и которая находится под действием активных сил 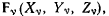заменим наложенные на систему связи силами реакции 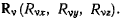После такой замены каждая точка системы должна рассматриваться как свободная от связей и находящаяся только под действием активных 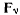сил и сил 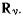Возможные перемещения такой освобожденной системы 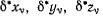уже не стеснены никакими условиями и поэтому все являются произвольными и независимыми. Принцип Бернулли для этой системы представляется в виде равенства

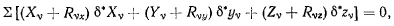
откуда в силу независимости величин 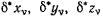следуют уравнения

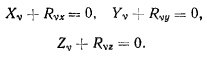
Принцип возможных перемещений дает возможность определять положения равновесия системы материальных точек, не определяя реакции связей.

Если существует силовая функция для сил, действующих на систему материальных точек, то принцип Бернулли получает особенно простой вид. В этом случае имеем

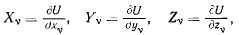
а потому условие равновесия преобразуется к виду

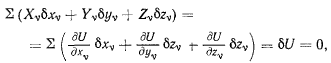
или

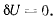
Это условие говорит о том, что в положении равновесия силовая функция имеет стационарное значение для всех неосвобождаю-щих перемещений системы.

Пример:

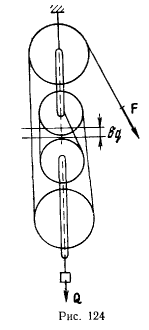
Полиспаст (механизм, состоящий из двух блоков, каждый из которых смонтирован в обшей обойме, причем блоки насажены на общую ось или на отдельные оси), как показано на рис. 124, оснащен нитью, один конец которой прикреплен к неподвижной точке, а другой остается свободным. Нить обходит последовательно все блоки, насаженные как на подвижные, так и на неподвижные оси. К нижнему блоку подвешен груз весом Q, а к свободному концу нити приложена сила F, которая должна уравновесить груз Q. Определить соотношение величин силы F и веса Q при равновесии системы.

Решение:

Предположим, что размеры блоков подобраны так. что все части нити, заключенные между обеими системами блоков, можно рассматривать как параллельные. Тогда при перемещении точки приложения силы F на расстояние 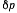груз поднимется на величину 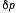Общая длина нити остается неизменной, так что

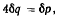
как это видно из чертежа. Из принципа Бернулли для двусторонних связей имеем

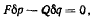
или после подстановки значении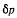

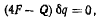
откуда сразу получаем условие равновесия

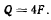
Пример:

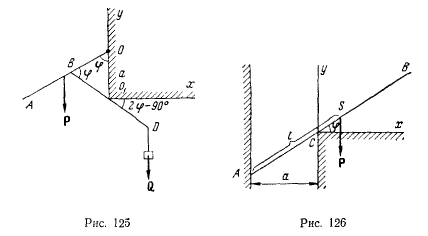
Два однородных стержня BD и OA соответственно длиной 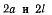и весом Р каждый могут свободно вращаться в одной вертикаль-кон плоскости: первый вокруг своей середины 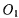второй вокруг шарнира О. расположенного на одной вертикали с 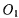на расстоянии а от точки 0( (рис. 125). К концу D стержня BD прикреплен груз Q. Определить угол 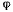в положении равновесия системы.

Решение:

Активные силы Р и Q имеют проекции только на вертикальную ось у, поэтому из принципа Бернулли будем иметь

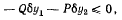
где знак неравенства имеет место только для освобождающих перемещений. Рассматривая сначала только не освобождающие перемещения, координаты 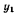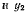представим в функции угла 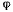т. е.

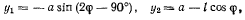
откуда

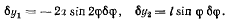
После подстановки найденных вариаций координат будем иметь

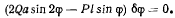
Откуда получаем значения угла 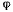в положении равновесия:

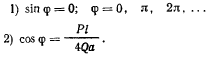
Первая система значений 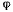представляет особое решение и не допускается наложенными на систему связями. Второе решение имеет смысл тогда, когда

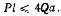
Переходя к анализу освобождающих перемещений, которые могут появиться только при потере контакта между стержнями, заметим, что здесь сумма работ всех активных сил всегда будет отрицательна, так как освобождение сопровождается либо поднятием груза Q, либо поворотом вверх стержня OA. Таким образом, рассмотренное положение является положением равновесия

Пример:

Однородный гладкий стержень АВ длиной 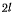и весом Р опирается одним концом на гладкую вертикальную стенку и, кроме того, опирается в точке С на край неподвижною стола (рис. 126). Определить угол 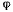который образует стержень со столом в положении равновесия, если расстояние от стенки до стола равно а.

Решение:

Если центр тяжести находится слева от точки С, равновесия быть не может, так как при освобождении точки А работа силы тяжести станет положительной. Для определения положения равновесия, когда точка S находится справа от точки С, из принципа Бернулли, рассматривая не освобождающие перемещения, имеем

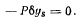
Подставляя сюда значение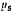

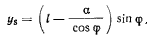
будем иметь

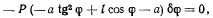
отсюда, приравнивая нулю выражение, стоящее в скобках, получаем условие равновесия

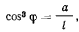
которое возможно лишь при условии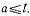

Пример:

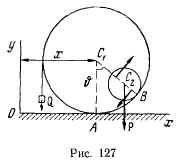
В полый цилиндр радиуса R, который может кататься без скольжения по горизонтальной плоскости, вложен массивный цилиндр лесом Р с радиусом r (рис. 127). К малому цилиндру в плоскости чертежа приложена пара сил с моментом М. На полый цилиндр намотана нить, несущая на свободном конце груз Q. Полагая поверхности цилиндров достаточно шероховатыми, найти положение равновесия системы и определить, при какой зависимости между данными силами оно возможно.

Решение:

Положение системы полностью определяется двумя координатами х и 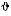. которые могут изменяться независимо одна от другой. Поэтому любое возможное перемещение системы будет определяться изменением этих двух независимых координат. Сообщим сначала большому цилиндру такое возможное перемещение, при котором не изменяется угол 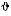(малый цилиндр при этом вращается вокруг своей осн. перемещаясь в горизонтальном направлении). На этом перемещении сила Р не совершает работы. Обозначим через х горизонтальную координату центра большого цилиндра и подсчитаем работу силы Q и пары М на рассматриваемом перемещении. Сила Q

будет совершать отличную от нуля работу лишь при перемещения груза в вертикальном направлении. Если центр большого цилиндра переместится на

величину 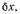то сам цилиндр повернется вокруг своей оси на угол 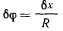(на чертеже не указан). При этом провисающая часть нити сократится на величину 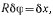а сила Q совершит работу — 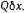Точка В большого цилиндра (точка касания) повернется от вращения вокруг его оси 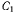на

величину 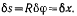На такую же величину повернется и точка В малого цилиндра, вращающегося вокруг своей оси 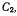сам же цилиндр повернется на угол 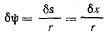(на чертеже не указан). Как нетрудно видеть, пара сил, действующих на малый цилиндр, совершит положительную работу 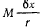(работа пары сил на поступательном перемещении сплошного цилиндра всегда равна нулю).

Приравнивая нулю работу всех сил, действующих на систему, получим

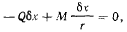
откуда следует условие равновесия

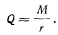
Сообщим теперь системе такое «возможное перемещение, при котором координата х остается постоянной, а изменяется только угол 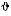Заметим, что при таком перемещении сила Q не будет совершать работы (отсутствует перемещение точки приложения силы). Работа силы Р на рассматриваемом перемещении будет равна

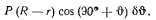
При вычислении работы пары сил заметим, что малый цилиндр при таком перемещении будет катиться без скольжения по поверхности большого, вращаясь вокруг своей осн. Мгновенное перемещение малого цилиндра можно представить как сумму мгновенно-поступательного перемещения вместе с осью и мгновенного вращения вокруг этой оси. На поступательном перемещении пара сил работы не совершает. Обозначая угол поворота малого цилиндра относительно неподвижных осей через получим для этого угла выражение

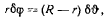
а работа пары сил будет равна

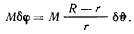
Из принципа Бернулли теперь получим

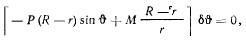
откуда

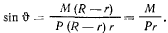
Действительное значение для угла 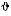существует лишь при условии

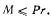
Мы рассмотрели все возможные перемещения системы и получили все возможные положения равновесия.

Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:

Предмет теоретическая механика

Эти страницы возможно вам будут полезны:

Сила тяжести

Упругая сила

Принцип Торричелли

Связи и возможные перемещения