Оглавление:
Принцип возможных перемещений
Пусть мы имеем несвободную систему материальных точек, находящуюся в равновесии под действием всех приложенных к ней активных сил и сил реакций наложенных на нее идеальных связей.
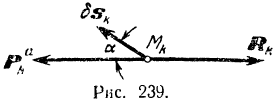
Выделим произвольную точку 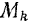 этой системы. Равнодействующую всех приложенных к ней активных сил обозначим через
этой системы. Равнодействующую всех приложенных к ней активных сил обозначим через 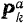 и равнодействующую всех реакций наложенных на нее связей — через
и равнодействующую всех реакций наложенных на нее связей — через 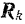 . Так как выделенная точка находится в равновесии вместе со всей системой, то две приложенные к ней силы
. Так как выделенная точка находится в равновесии вместе со всей системой, то две приложенные к ней силы 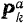 и
и 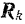 должны быть направлены в противоположные стороны и равны по модулю. Сообщая системе возможное перемещение, отметим перемещение
должны быть направлены в противоположные стороны и равны по модулю. Сообщая системе возможное перемещение, отметим перемещение 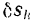 , (рис. 239), получаемое при этом точкой
, (рис. 239), получаемое при этом точкой 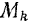 , системы.
, системы.
Составляя сумму элементарных работ всех сил, приложенных к точке 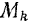 на ее возможном перемещении, получим:
на ее возможном перемещении, получим:
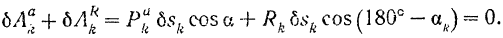
Написав подобные равенства для всех точек системы и просуммировав их, получим:
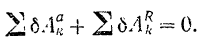
Но для идеальных связей согласно самому их определению всегда
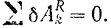
Следовательно, при равновесии системы с идеальными связями
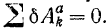
Нетрудно доказать справедливость и обратного положения.
Если для какой-либо системы с идеальными связями
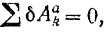
то эта система находится в равновесии.
Таким образом, мы приходим к весьма важному принципу механики, называемому принципом возможных перемещений.
Для равновесия системы с идеальными связями необходимо и достаточно, чтобы равнялась нулю сумма элементарных работ всех приложенных к ней активных сил на всяком возможном перемещении, системы из положения равновесия
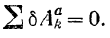
Пользуясь выражением (189) элементарной работы, условию (215) равновесия системы с идеальными связями можно придать другую форму:
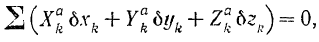
где 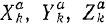 — проекции на оси координат, приложенных к системе активных сил;
— проекции на оси координат, приложенных к системе активных сил; 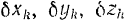 — элементарные приращения координат
— элементарные приращения координат 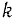 -й точки системы па возможном перемещении этой точки.
-й точки системы па возможном перемещении этой точки.
Принцип возможных перемещений выражает необходимые и достаточные условия равновесия не только абсолютно твердого тела, но и любых систем материальных точек. Особенно удобно пользоваться им в случаях, когда находящаяся в равновесии система состоит из большого числа связанных между собой тел. Решение задачи о равновесии такой системы при помощи уравнений равновесия, даваемых геометрической статикой, весьма громоздко. Приходится мысленно расчленять систему на отдельные тела и заменять наложенные на них связи неизвестными реакциями. Это приводит к составлению большого числа уравнении со многими неизвестными.
В уравнения же (215) и (216), выражающие принцип возможных перемещений, реакции идеальных связей не входят вообще. Данными уравнениями можно пользоваться и тогда, когда трением в связях пренебречь нельзя.
В этом случае при применении уравнений (215) и (216) надо отнести силы трения к категории активных сил.
Число условий равновесия системы равно числу ее степеней свободы. Если система имеет, как чаще всего бывает в практических задачах, только одну степень свободны то одно из равенств (215) или (216) устанавливают единственное условие равновесия такой системы.
При решении задачи методом возможных перемете ним нужно составить схему всех приложенных к систему активных сил, включая в их число и силы трения (когда ими пренебречь нельзя).
Если задача решается геометрически, с помощью уравнения (215), то, сообщив одной из точек системы возможное перемещение, нужно показать па схеме векторы 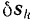 соответствующих перемещений точек приложения всех действующих на систему активных сил и углы
соответствующих перемещений точек приложения всех действующих на систему активных сил и углы 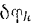 соответствующих поворотов тел, па которые действуют активные силы. Записав уравнение (215) элементарных работ всех активных сил на соответствующих возможных перемещениях, нужно найти зависимость между величинами
соответствующих поворотов тел, па которые действуют активные силы. Записав уравнение (215) элементарных работ всех активных сил на соответствующих возможных перемещениях, нужно найти зависимость между величинами 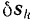 и
и 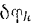 вошедшими в уравнение, выразив их все через одну или найдя соотношение между ними. После этого мы получаем уравнение, из которого легко находятся искомые величины.
вошедшими в уравнение, выразив их все через одну или найдя соотношение между ними. После этого мы получаем уравнение, из которого легко находятся искомые величины.
Если задача решается аналитически, с помощью уравнения (216), то нужно выбрать неподвижные по отношению к рассматриваемой системе оси координат. Затем найти проекции 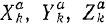 на эти оси каждой из активных сил и координаты
на эти оси каждой из активных сил и координаты 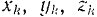 их точек приложения. Выразив последние в виде функций обобщенных координат системы, путем дифференцирования их по этой обобщенной координате, находят элементарные приращения
их точек приложения. Выразив последние в виде функций обобщенных координат системы, путем дифференцирования их по этой обобщенной координате, находят элементарные приращения 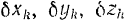 , координат точек приложения данных сил па возможном перемещении этих точек.
, координат точек приложения данных сил па возможном перемещении этих точек.
В случае, когда система обладает несколькими степенями свободы, уравнения (215) и (216) надо составлять для каждого независимого перемещения отдельно, считая при этом возможные перемещения, соответствующие другим степеням свободы, равными нулю. Искомая величины в этом случае определяются из совместного решения уравнении равновесия, число которых должно быть равно числу степеней свободы рассматриваемой системы.
Принципом возможных перемещений можно пользоваться и для определения реакций связей. В частности, и в том случае, когда система представляет собой жесткую конструкцию, не обладающую ни одной степенью свободы.Для определения реакции какой-либо связи, наложенной на систему, мысленно отбрасывают эту связь, заменяя ее действие на систему реакцией связи к включая ее в число активных сил, действующих на систему. Сообщая системе, освобожденной от одной связи, возможное перемещение, составляют уравнение работ (215) или (216), из которого и определяется искомая реакция связи.
Пример задачи:
В гидравлическом прессе (рис. 240) диаметр малою цилиндра 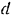 , диаметр большого цилиндра
, диаметр большого цилиндра 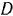 . Пренебрегая трением, определить усилие
. Пренебрегая трением, определить усилие 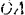 , перпендикулярно к его длине. для того чтобы уравновесить силу
, перпендикулярно к его длине. для того чтобы уравновесить силу 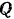 сопротивления сжимаемого тела
сопротивления сжимаемого тела
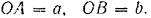
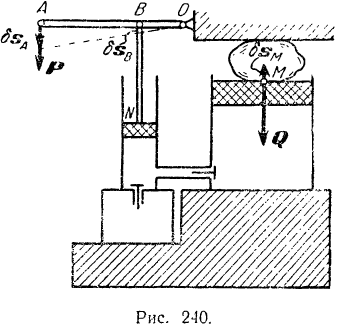
Решение:
Рассматривая систему как находящуюся в, равновесии под действием сил 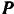 и
и 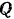 , сообщим рычагу
, сообщим рычагу 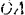 возможное перемещение— поворот па бесконечно малый угол вокруг точки
возможное перемещение— поворот па бесконечно малый угол вокруг точки 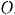 . При этом точка
. При этом точка 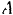 приложены силы
приложены силы 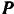 получит возможное перемещение
получит возможное перемещение 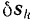 совпадающее с направлением силы
совпадающее с направлением силы 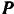 , а точка
, а точка 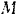 приложения силы
приложения силы 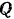 — перемещение
— перемещение 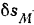 противоположное направлению силы
противоположное направлению силы 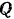 . Применяя к равновесию системы принцип возможных перемещений, составим уравнение (215):
. Применяя к равновесию системы принцип возможных перемещений, составим уравнение (215):
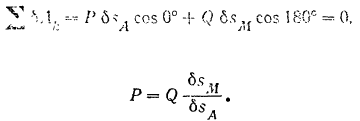
Для того чтобы найти отношение 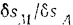 возможных перемещений точек
возможных перемещений точек 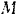 и
и 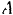 , найдем сначала соотношения между возможными перемещении точек
, найдем сначала соотношения между возможными перемещении точек 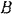 и
и 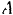 рычага и точек
рычага и точек 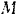 и
и 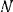 порошей пресса.
порошей пресса.
Перемещения 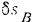 и
и 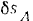 пропорциональны расстояниям точек
пропорциональны расстояниям точек 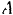 и
и 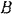 рычага от его оси
рычага от его оси 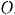 вращении:
вращении:
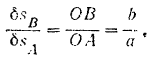
Объем жидкости, вытесняемой малым поршнем при его перемещении вниз на величину
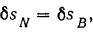
равен
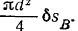
жидкости, поступающей при этом в большой цилиндр, равен
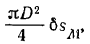
где 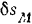 — перемещение большого поршня, соответствующее перемещению
— перемещение большого поршня, соответствующее перемещению 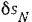 малого поршня. Из очевидного равенства этих объемов имеем:
малого поршня. Из очевидного равенства этих объемов имеем:
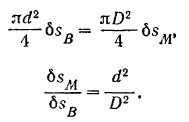
Перемножая правые и левые части равенств (II) и (III), получим:
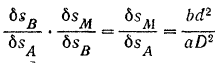
Подставляя найденное выражение (IV) в равенство значение искомого усилия:
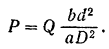
Пример задачи:
В кулисном механизме (рис. 241) при качании кривошипа 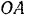 вокруг горизонтальной оси
вокруг горизонтальной оси 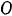 ползун
ползун 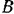 , перемещаясь вдоль кривошипа
, перемещаясь вдоль кривошипа 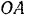 , приводит в движение ползун
, приводит в движение ползун 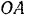 , движущийся в вертикальных направляющих. Найти, какой момент
, движущийся в вертикальных направляющих. Найти, какой момент 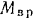 сил относительно оси вращения при данном угле
сил относительно оси вращения при данном угле 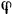 поворота кривошипа надо приложить к кривошипу, чтобы уравновесить вертикальную силу
поворота кривошипа надо приложить к кривошипу, чтобы уравновесить вертикальную силу 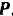 . приложенную к ползуну
. приложенную к ползуну 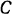 . Расстояние
. Расстояние 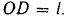
Решение:
Дадим кривошипу 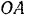 возможное перемещение — поворот на элементарный угол
возможное перемещение — поворот на элементарный угол 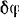 . Тогда по формуле (200) элементарная работа силы, приложенной к кривошипу:
. Тогда по формуле (200) элементарная работа силы, приложенной к кривошипу:
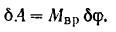
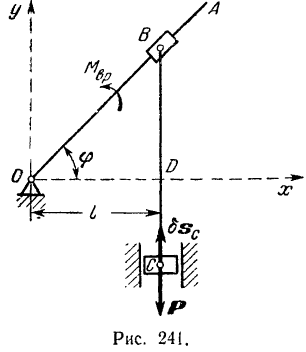
При указанном на рис. 241 направления вращения кривошипа возможное перемещение 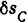 точки приложения силы
точки приложения силы 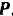 будет направлено вертикально вверх, т. е. в сторону, противоположную направлению этой силы.
будет направлено вертикально вверх, т. е. в сторону, противоположную направлению этой силы.
Составляя уравнение (213) равновесия системы, будем иметь:
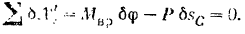
Выразим перемещение 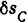 через обобщенную координату
через обобщенную координату 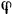 . Возможное перемещение
. Возможное перемещение 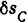 ползуна
ползуна 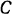 равно вертикальному перемещению точки
равно вертикальному перемещению точки 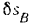 кривошипа. Из рис. 241 находим ординату точки
кривошипа. Из рис. 241 находим ординату точки 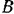 :
:
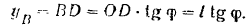
Отсюда, дифференцируя это выражение по 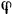 , получим
, получим
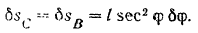
Подставляя найденное значение 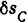 в уравнение равновесия, будем иметь:
в уравнение равновесия, будем иметь:
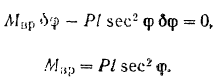
Пример задачи:
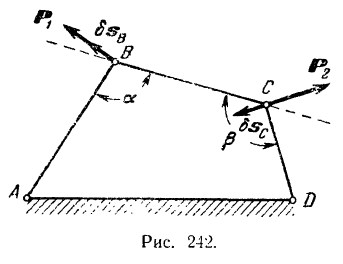
К шарнирному четырехзвеннику 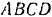 (рис. 242), звено , которого неподвижно, а точке
(рис. 242), звено , которого неподвижно, а точке 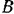 приложена сила
приложена сила 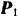 , перпендикулярная к звену
, перпендикулярная к звену 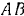 , и в точке
, и в точке 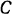 — сала
— сала 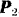 , перпендикулярная к звену
, перпендикулярная к звену 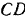 . Найти зависимость между модулями сил
. Найти зависимость между модулями сил 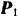 и
и 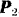 , если четырехзвенник находится и равновесии и углы
, если четырехзвенник находится и равновесии и углы 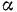 и
и 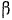 известны.
известны.
Решение:
Нарушим мысленно равновесие системы, повернув на бесконечно малый угол звено 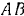 . Точка
. Точка 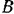 приложения силы
приложения силы 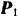 , получит при этом элементарное перемещение
, получит при этом элементарное перемещение 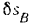 , совпадающее с направлением силы
, совпадающее с направлением силы 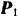 , и точка
, и точка 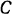 приложения силы
приложения силы 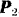 — элементарное перемещение
— элементарное перемещение 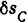 противоположное направлению силы
противоположное направлению силы 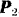 .
.
Составляя уравнение равновесия системы, получим:
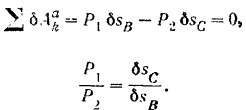
Перемещения 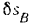 и
и 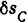 точек
точек 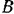 и
и 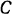 звена
звена 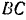 пропорциональны скоростям этих точек. По теореме же о проекциях скоростей двух точек фигуры на прямую, соединяющую эти точки (§ 62), мы имеем:
пропорциональны скоростям этих точек. По теореме же о проекциях скоростей двух точек фигуры на прямую, соединяющую эти точки (§ 62), мы имеем:
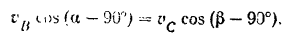
Отсюда находим:
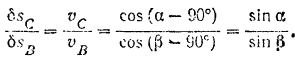
Заменяя правую часть равенства (I) найденным ее значением (II), находим:
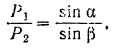
Пример задачи:
Однородный стержень 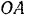 (рис. 243) весом
(рис. 243) весом 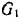 может вращаться на неподвижном шарнире
может вращаться на неподвижном шарнире 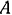 в вертикальной плоскости. Конец
в вертикальной плоскости. Конец 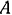 этого стержня соединен шарниром
этого стержня соединен шарниром 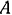 с другим однородным стержнем
с другим однородным стержнем 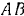 , вес которого
, вес которого 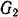 . К концу
. К концу 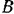 второго стержня приложена горизонтальная сила
второго стержня приложена горизонтальная сила 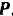 . Пренебрегая трением в шарнирах, найти углы
. Пренебрегая трением в шарнирах, найти углы 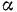 и
и 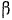 , которые стержни
, которые стержни 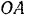 и
и 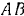 составляют с горизонталью при равновесии системы.
составляют с горизонталью при равновесии системы.
Решение:
Для решения задачи воспользуемся уравнением равновесия системы в форме:
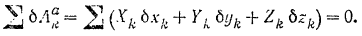
Примем неподвижную точку 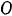 за начало координат и проведем оси координат так, как показано на рис. 243. Проекции на эти оси приложенных к системе активных сил:
за начало координат и проведем оси координат так, как показано на рис. 243. Проекции на эти оси приложенных к системе активных сил:
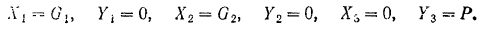
Уравнение равновесия принимает при этом вид
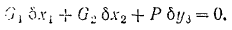
Координаты точек приложения данных сил будут:
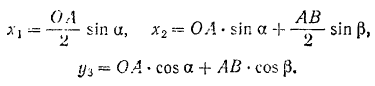
Рассматриваемая система имеет две степени свободы, так как ее положение определяется двумя независимыми друг от друга возможными перемещениями: поворотом стержня 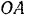 вокруг точки
вокруг точки 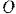 на элементарный угол
на элементарный угол 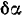 и поворотом стержня
и поворотом стержня 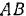 вокруг точки
вокруг точки 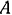 на элементарный угол
на элементарный угол 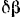 .
.
Составим уравнение (216) равновесия для каждого независимого перемещения отдельно, считая при этом другое возможное перемещение равным нулю.
1) Положим 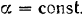 . Тогда, дифференцируя равенства (II) по
. Тогда, дифференцируя равенства (II) по 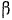 , найдем частные дифференциалы соответствующих координат:
, найдем частные дифференциалы соответствующих координат:
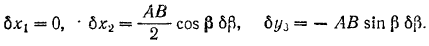
Подставляя эти значения в равенстве (I), получим:
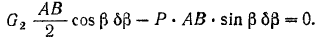
Отсюда, сокращая все члены последнего равенства на 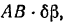 находим:
находим:
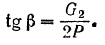
2) Положим 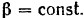 Дифференцируя равенства (II) по
Дифференцируя равенства (II) по 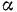 , находим соответствующие частные дифференциалы координат точек приложения сил:
, находим соответствующие частные дифференциалы координат точек приложения сил:
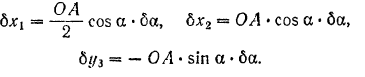
Подставляя эти значения в равенство (I), получим:
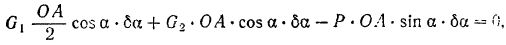
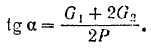
Пример задачи:
Составная балка 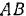 , лежащая на трех опорах, состоит из двух балок
, лежащая на трех опорах, состоит из двух балок 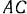 и
и 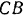 , шарнирно соединенных в точке
, шарнирно соединенных в точке 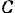 (рис. 244, а). К балке
(рис. 244, а). К балке 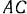 приложена пара сил с моментом
приложена пара сил с моментом 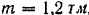 , направленным по ходу стрелки часов, и в точке
, направленным по ходу стрелки часов, и в точке 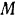 вертикальная сила
вертикальная сила 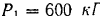 . К балке
. К балке 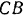 в точке
в точке 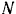 приложена вертикальная сила
приложена вертикальная сила 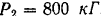 . Даны размеры:
. Даны размеры:
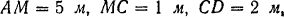
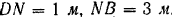
Пользуясь принципом возможных перемещений, определить реакции опор 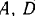 и
и 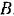 . Весом балок пренебречь.
. Весом балок пренебречь.
Решение:
1) Для определения реакции опоры 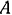 мысленно отбросим эту опору и заменим ее действие на балку реакцией
мысленно отбросим эту опору и заменим ее действие на балку реакцией 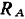 данной опоры. Теперь балку можно рассматривать как систему с одной степенью свободы, находящуюся в равновесии под действием приложенных к ней активных сил и реакции
данной опоры. Теперь балку можно рассматривать как систему с одной степенью свободы, находящуюся в равновесии под действием приложенных к ней активных сил и реакции 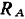 связи. Возможным перемещением этой системы без нарушения остающихся связей (шарнира
связи. Возможным перемещением этой системы без нарушения остающихся связей (шарнира 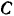 и опор
и опор 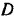 и
и 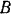 ) будет поворот балки
) будет поворот балки 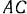 вокруг шарнира
вокруг шарнира 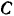 на элементарный угол
на элементарный угол 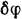 . Предположим, что этот поворот совершается по ходу стрелки часов (рис. 244,6). Тогда элементарное перемещение
. Предположим, что этот поворот совершается по ходу стрелки часов (рис. 244,6). Тогда элементарное перемещение 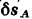 точки
точки 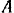 приложения силы
приложения силы 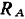 будет совпадать с направлением этой силы и ее работа будет положительной. Элементарное же перемещение
будет совпадать с направлением этой силы и ее работа будет положительной. Элементарное же перемещение 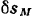 точки
точки 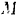 приложения силы
приложения силы 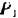
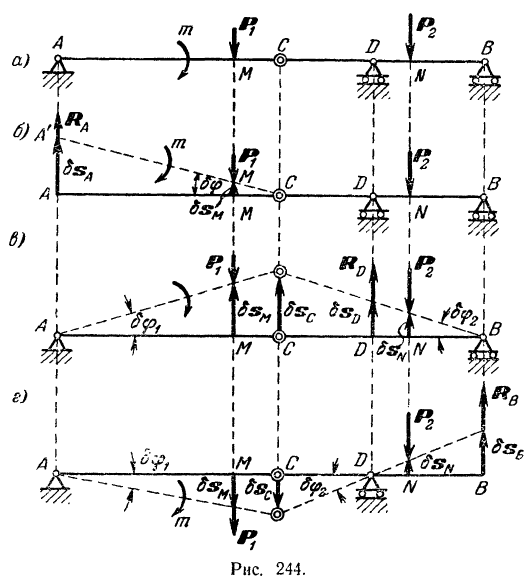
будет противоположно направлению силы и ее работа будет отрицательной. Работа силы 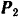 будет равна пулю, так как точка
будет равна пулю, так как точка 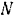 приложения этой силы не перемещается вовсе при данном возможном перемещении системы. Так как принятое направление поворота балки
приложения этой силы не перемещается вовсе при данном возможном перемещении системы. Так как принятое направление поворота балки 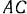 совпадает с заданным направлением вращения пары, то элементарная работа пары согласно формуле (200) равна
совпадает с заданным направлением вращения пары, то элементарная работа пары согласно формуле (200) равна 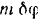 и будет положительной.
и будет положительной.
Составляя уравнение (215) равновесия системы, будем иметь:
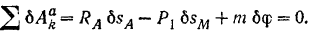
Из 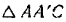 (рис. 244,6) находим:
(рис. 244,6) находим:
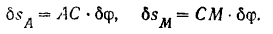
Подставляя эти значения о равенство (I), получим
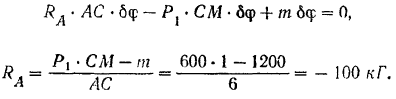
Знак минус показывает, что реакция 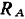 направлена в действительности не вверх, как было предположено, а вниз.
направлена в действительности не вверх, как было предположено, а вниз.
2) Для определения реакции 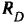 опоры
опоры 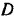 отбрасываем эту опору и заменяем ее действие на балку реакцией
отбрасываем эту опору и заменяем ее действие на балку реакцией 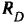 этой опоры. Давая полученной системе возможное перемещение (рис. 244, в), составляем для нее уравнение равновесия:
этой опоры. Давая полученной системе возможное перемещение (рис. 244, в), составляем для нее уравнение равновесия:
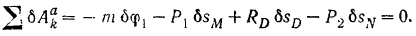
Здесь, перед выражением работы 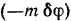 пары сил, взят знак минус, таи как заданное направление вращения пары в данном случае противоположно предположенному (рис. 244. в) направлению поворота балки
пары сил, взят знак минус, таи как заданное направление вращения пары в данном случае противоположно предположенному (рис. 244. в) направлению поворота балки 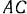 (против часовой стрелки).
(против часовой стрелки).
Выразим возможные перемещения точек приложения всех сил через какой-нибудь один параметр, например, через угол поворота 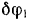 . Предварительно найдем зависимость между углом
. Предварительно найдем зависимость между углом 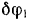 , поворота балки
, поворота балки 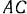 и соответствующим ему углом
и соответствующим ему углом 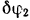 поворота балки
поворота балки 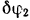 .
.
Из рис. 244, в имеем:
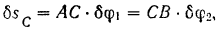
откуда
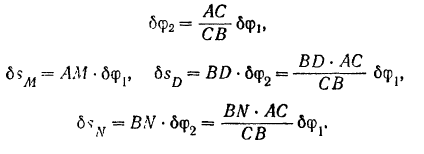
Подставляя найденные значения перемещений в равенство (II), получим:
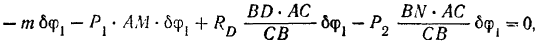
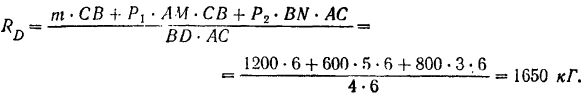
3) Отбрасывая опору 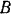 и давая системе возможное перемещение, составляем уравнение равновесия:
и давая системе возможное перемещение, составляем уравнение равновесия:
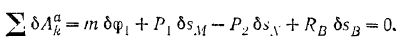
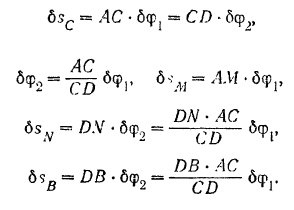
Подставляя найденные значения перемещений в равенство (III), получим
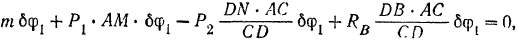
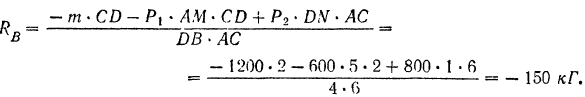
Знак минус показывает, что реакция 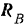 должна быть направлена вниз, а не вверх, как было предположено.
должна быть направлена вниз, а не вверх, как было предположено.
Определив методом возможных перемещений реакции двух опор, реакцию третьей опоры проще было бы найти, использовав уравнение равновесия статики для плоской системы параллельных сил:
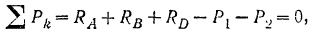
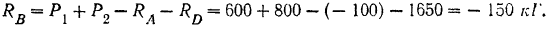
Данную задачу можно было бы, конечно, и целиком решить методом статики твердого тела. Для этого надо было бы расчленить мысленно балку 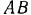 на две балки
на две балки 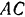 и
и 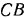 . заменив действие шарнира
. заменив действие шарнира 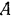 на каждую из них его реакциями. Затем составить для каждой из балок соответствующие уравнения равновесия статики и совместно решить полученную систему уравнений.
на каждую из них его реакциями. Затем составить для каждой из балок соответствующие уравнения равновесия статики и совместно решить полученную систему уравнений.
При сложных системах, особенно когда не требуется определять реакции всех связей, метод возможных перемещений дает более короткое решение задачи.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

