Принцип Торричелли

Принцип Торричелли

В качество примера на применение принципа Бернуллн рассмотрим известный принцип Торричелли, устанавливающий условия равновесия тяжелых тел. В 1G44 г. итальянский физик Еванджелиста Торричелли (1608-1647) сформулировал принцип равновесия системы тяжелых тел (системы тел, находящихся под действием только сил тяжести), заключающийся в том, что в положении равновесии центр тяжести системы занимает наинизшее из возможных положение. Принцип Торричелли отбирает из всех возможных положений равновесия только устойчивые. Обобщение этого принципа можно непосредственно получить из принципа Бернуллн. В самом деле, пусть на систему материальных точек 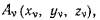стесненную идеальными двусторонними связями, действуют только силы тяжести 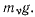Выберем систему прямоугольных осей 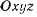таким образом, чтобы ось z была направлена вертикально вверх. Тогда для проекций активных сил на эти оси будем иметь

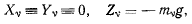
поэтому принцип Бернуллн получает вид

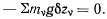
В силу соотношения

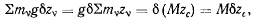
где 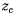— координата центра тяжести системы, предыдущее равенство перепишется в виде

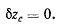
Отсюда следует, что в положении равновесия координата 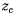центра тяжести системы имеет стационарное значение. Система будет находиться в равновесии, если при всех возможных перемещениях системы ее центр тяжести не перемешается по вертикали.

Пример:

Палочка АВ длиной 2а и песом Р концом А опирается на плоскость (я), образующую угол а с горизонтом, а в точке С — на острие (рис. 128). Определить угол <р между палочкой и горизонтом при равновесии. Размеры и расположение плоскости и острия указаны на чертеже.

Решение:

Возможное перемещение палочки сводится к повороту вокруг мгновенного центра S, расположенного в точке пересечения нормалей к плоскости (я) и к палочке. Из всех точек палочки только перемещение точки D, находящейся иа одной вертикали с точкой S, горизонтально. Как

следует из принципа Торричелли, палочка будет находиться в равновесии лишь в том случае, когда ее центр тяжести будет находиться в точке D.

Для получения аналитического решения определим сначала координату 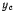центра тяжести палочки:

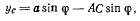
где

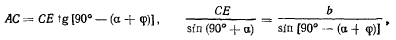
тогда

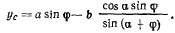
При бесконечно малом возможном перемещении палочки координата у получит приращение

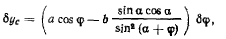
которое в соответствии с принципом Торричелли должно обращаться в нуль R положении равновесия, т. е.

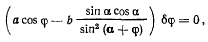
откуда для определения угла 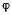получаем уравнение

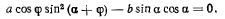
Пример:

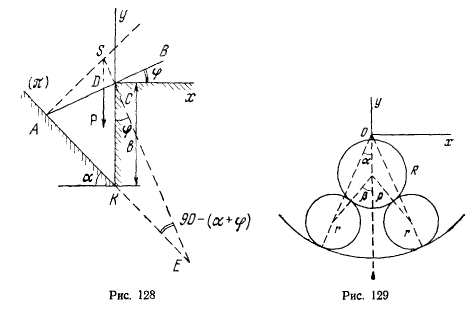
Два одинаковых цилиндра весом р каждый положены на внутреннюю поверхность полого цилиндра. Они поддерживают третий цилиндр веса q (рис. 129). Определить зависимость между углами аир при равновесии системы. Размеры указаны на чертеже.

Решение:

Выберем систему осей Оху с началом в центре неподвижного цилиндра. Ось у направим вертикально вверх. Тогда координата 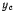центра тяжести системы определится из равенства

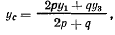
где 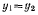координаты центров тяжести нижних цилиндров: 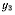— координата центра тяжести верхнего цилиндра. Тогда в силу симметрии будем иметь

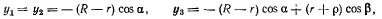
где R —радиус полого цилиндра; r — радиусы нижних цилиндров, р — радиус верхнего цилиндра. Тогда

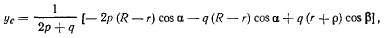
и из принципа Торричелли получим

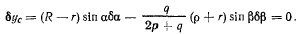
Параметры а и 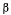связаны соотношением

сохраняющимся при всех возможных перемещениях системы. Поэтому будем иметь зависимость

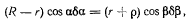
получающуюся непосредственным дифференцированием соотношения (b) Исключая из уравнений (а) и (с) величину 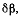получим после сокращения на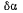

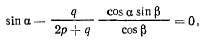
откуда

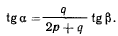
Эта лекция взята со страницы, где размещены все лекции по предмету теоретическая механика:

Предмет теоретическая механика

Эти страницы возможно вам будут полезны:

Упругая сила

Принцип возможных перемещения

Связи и возможные перемещения

Обобщенные координаты