Оглавление:













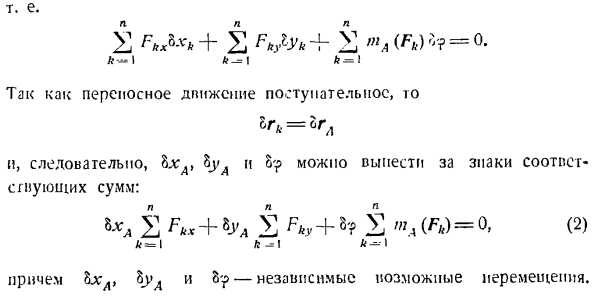




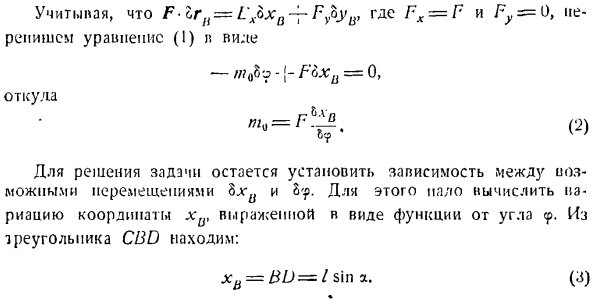



























Принцип возможных перемещений
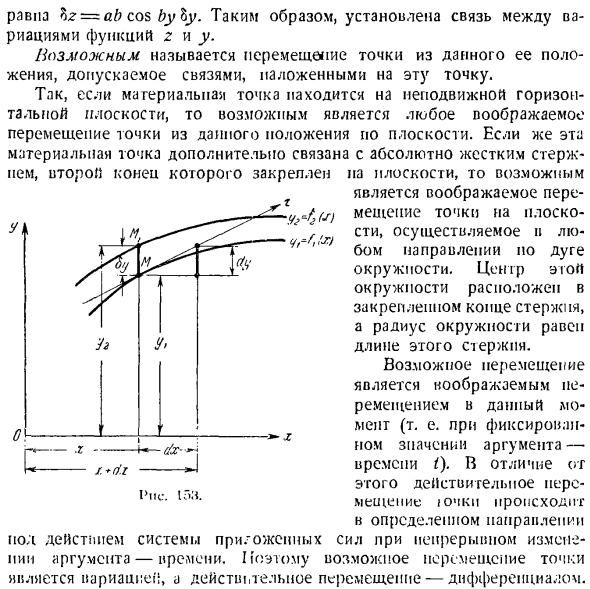
- Принцип возможного движения 1°.Возможное движение. Идеальное соединение. Вариация функции bj-это приращение функции, обусловленное изменением функции saw на фиксированное значение argument. So, при переходе от функции y} = f, (l’) к функции (l*) вариация функции 8y выглядит следующим образом: На = Г * — Э-э = / 2(л)-л(л). В отличие от изменения функции 8y, дифференциал функции dy является основной частью приращения функции, образованной приращением аргумента dx. Рис. in в, сегмент MMC численно равен вариации функции B, соответствующей фиксированному значению аргумента B. На этом же рисунке показано, что сегмент, численно равный производной функции DY, соответствует приращению значения аргумента X ^ — DX.
Правила для различных признаков внешне аналогичны соответствующим правилам для дифференцирования признаков. Таким образом, σ (ω) — c-постоянная, δ, γ (±)= Sy, γ — °(j/, γ<γ= yx, y-y£y\ и т. д) Комплексная функция z = o (y \ y = f (x), флуктуации которого определяются по формуле bz = ^ by. Например, z = as \ nby. Где y-функция изменения x. Z Гораздо проще решить эту проблему, используя принцип возможного смещения. Давайте покажем заданные силы Р и F на рисунке. Дайте точке B бицепса возможное движение L2 = BB и вертикально upwards. In в этом случае верхний рычаг вращается по часовой стрелке вокруг точки О, а нижний-в том же направлении. Голы: 377 , oRD = DDx, в зависимости от Ln (на рисунке новое положение рычага обозначено пунктирной линией).
Выразим возможное смещение точки D нижнего рычага Людмила Фирмаль
Используя подобие треугольников, построенных на верхнем плече, вы можете написать следующее: 8gd =—og / g как стержень является полностью жестким стержнем, так и ogs = 8g, то есть это жесткий стержень. ФКП = сокр. (1) Исходя из подобия треугольников, построенных на нижнем плече, это выглядит так: b0 = Y. подставляя значение bc из выражения (I), получаем: 4 =(2) Принцип возможного смещения применяется к рычажной системе. То есть возможны смещения точек B и D приложения КРД, а сумма работы заданных сил F и P от b0 равна нулю: FbrB-Pbgv =0.(3) Используя выражение (2) и сжимая выражение (3) na ogv, вы получаете: ’ч’ «=[- А)Р-(4)
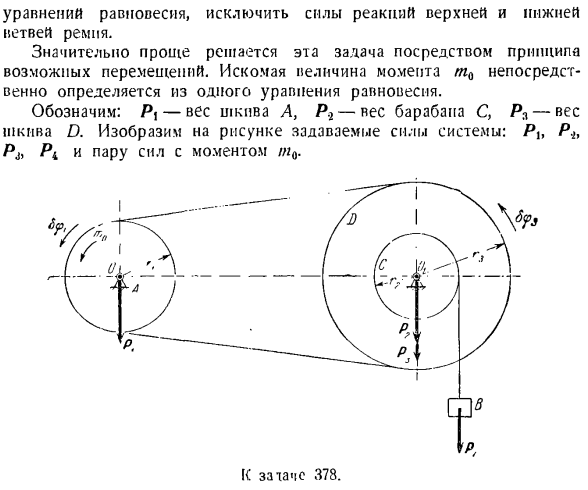
Если подставить число, то получится результат: P = 1000 kg. To решите эту задачу, если вы дадите возможное движение RQ к точке B вниз, а не вверх, знак в уравнении (3) изменится противоположно. вместо возможного линейного смещения точки bg можно было дать возможное угловое смещение k = ; * СП、 \ Дж То есть запишите результат и Формулу(4). Задача 378.На рисунке показана ременная передача для соединения шкива A и D. радиус r определяет момент/ 0 силы, приложенной к шкиву a{для уравновешивания нагрузки B весом P4.Груз B привязан к концу троса, обернутого вокруг барабана C радиуса r, связанного со шкивом D радиуса r 3.
- Масса ремня и веревки игнорируется. Solution. To для решения этой задачи необходимо использовать статические методы, чтобы мысленно разрушить верхнюю и нижнюю ветви ремня и заменить их действие соответствующей силой связывающей реакции. Далее рассмотрим равновесие шкива A. шкив A — это уравнение момента относительно точки O, а шкив D и барабан C и масса Z? Это краткое изложение следующего. Их уравнения моментов указывают на 0 {для определения нужного момента требуется mQ. Уравнение равновесия исключает силу реакции верхней и нижней ветвей пояса.
Эта задача решается гораздо проще по принципу возможного движения. Значение, полученное для момента rnQ, определяется непосредственно из уравнения равновесия 1. Pj вес шкива a, P. 2-вес барабана C, Pl-вес шкива D. давайте покажем мощность системы на диаграмме. In в этом случае шкив d получает возможное угловое смещение в том же направлении. Если ремень шире и не скользит, напишите следующее: Р, 5?л = РСС ’ Ф3. (Я) Груз в получает возможность вертикального перемещения винта Sr4<.
Рассмотрим угловое движение шкива против часовой стрелки direction. Людмила Фирмаль
Bb = r2b. (2) Применяем принцип возможного смещения, то есть сумму работы данной силы к соответствующему возможному смещению точки приложения и делаем пулю равной: /// ОО’.;,- Р. {ОГ = 0.(3) (Гравитация ПБ п. 2 и задача ЛП-это равносильно пули. И это неудивительно, ведь точки их применения не сдвигаются. После сокращения на член выражения (I) и (2) с помощью pas (3)、
Задача 379.Используя принцип возможных перемещений, мы выводим уравнения равновесия свободных твердых тел под действием любых плоских сил. Решение. Нарисуем систему координат xy на рабочей поверхности силы. Указывает установленную силу: F] t Fb …сноска. Если выбрать любую точку а на полюсах рабочей поверхности заданной силы, то возможное движение твердого тела разложится на поступательное движение 6 / ^вместе с относительным вращением оси через точку а перпендикулярно рабочей поверхности силы и силы.
Переходим к выпуску 379. Применяя принцип возможного движения, можно: п- 2£мА (ФК) б> р =0.(1) к-ф. Один Сила FB Подходит…, Записал возможные смещения Fn и LK в разложении по единичному вектору осей x и Y. ПК = Pkx * — Т I7kvJ> ЛКК = bxj-л БЖ Дж、 Вот,£=!2,…вам, формат, (я) Иначе говоря £z7A + Си; / Ф-Ы АФ _ = и К = Л Перевод、 hgk = ГГЛ n, следовательно, bxA> bcn можно взять из знака соответствующей суммы. Часть 2 Fx * + «Ud t F» v + t ’» l нет.) =(2) В » = я к я Л-• Кроме того, & lgl, B> ’ l и o? Является возможность
независимого перемещения. Таким образом, левая часть уравнения (2) также исчезает п п п п п Коэффициент^ Fkxt ^ г] в иностранной валюте,^ ма(ФБ)、 k = > \ k = i b-стоя в этих возможных движениях i равно пуле, т. е. Эф * х = 0. = В ТП (б)=0.(3) k = 1 k = I L-I Как известно из статики, уравнение (3) является уравнением равновесия свободного твердого тела под действием произвольной плоской силы. Аналогично, если существует произвольная пространственная силовая система, то мы можем вывести 6 уравнений равновесия
свободных твердых тел. Полученные выше результаты убедительно подчеркивают степень общности принципа возможного смещения, который является мощным Средства для решения задачи статики. Проблема 380.Масса P {и радиус r при круговом эксцентриситете A вращается вокруг неподвижной горизонтальной оси O, перпендикулярной плоскости фигуры, масса P. 2. стержень B совершает возвратно-поступательное движение с вертикальной направляющей. Эксцентрик применяет момент против часовой
стрелки/ i — 1 бросьте точку на плоскости М> и М ^ ф / НТИ> ’Направление дуги. Центр этого круга находится на неподвижном конце стержня, а радиус круга равен длине этого стержня. Возможное движение-это виртуальное движение данного момента (то есть фиксированное значение аргумента-времени I).в отличие от этого, фактическое движение СКЛ происходит в определенном направлении под действием системы приложенных сил с непрерывным
изменением аргумента-времени. Таким образом, возможное смещение точки является вариацией, а фактическое смещение-производной. Рисунок 1g», время Точка D xD как функция угла поворота эксцентрика на угол а<р: хD = ОД = ОК—КД = значение COS 9г соѕ Ф (1) Где угол CD 0 представлен f. теперь установите соединение ■ 14 грехов 6 а Угол φ и Р К1 грехов 2? Ноль девять、 Bx0 = — грех(1-й ->.Cos 9) 09.(3)
Уравнение(3) устанавливает возможную кинетическую зависимость между 1×0 и ss5. Примените принцип возможного смещения к возможным механизмам. То есть сумма работы всех заданных сил на вероятное смещение точки системы будет равна нулю. И затем) Ф= Я \ грех
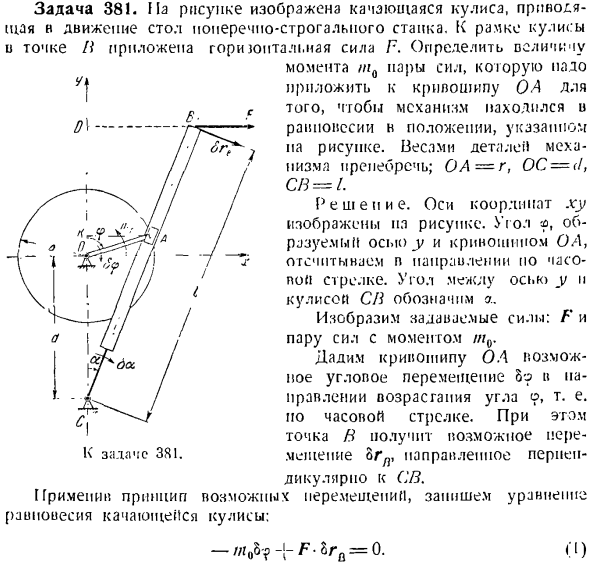
.с COS <Ф)грех <Ф> один Куда? Проблема 381.На этом рисунке показано коромысло, раскачивающее стол режущего аппарата. Горизонтальная сила F приложена к боковой рамке точки H. определяет значение В положении, показанном на рисунке момента силы, которая должна быть приложена к кривошипу ОА для того, чтобы механизм находился в равновесии. Игнорируйте вес деталей механизма. OA = r, OC = d, CB = L Решение. Оси xy показаны на рисунке. угол,
образованный осью y и кривошипом OA, отсчитывается по часовой стрелке. угол между осью y и кулисой совместного предприятия обозначается через a. Представляет собой совокупность сил: F и некоторых сил момента/ / / 0. Дает кривошипу ОА направление для увеличения угла о, То есть возможное угловое движение по часовой стрелке direction. In в этом случае точка B получает возможное смещение orfv, направленное перпендикулярно CB. Примените принцип возможного смещения и напишите уравнение
раскачивания крыла для раскачивания. Голы 381. П) F•Zr {{= L \ bxB-7-FfiyB, где FX = F и Fy = 0. рассмотрим формулу(!) — / ;? О п0-Джей-F6xB = 0、 Откуда Г-н БХП (2) * Для решения задачи остается установить связь между возможными движениями bx и k’.По этой причине необходимо рассчитать вариацию координаты chi, которая выражается в виде функции угла_d Вт грех = -7: — = Р * И4) В Ф греха — <Ф-р {(/- я•Р С COS <Ф) Дж Подставляя значение полученного греха в
уравнение(3), получаем: _ _ _ _ _ _ _ _ _ _ _ литий-ВР—ycF ^ ЛД?потому что 9′ С возможным движением КСК, вычисляя парящий Окси (р — ф д-4 — г в COS 9) потому что 9 4-й sin2o,…. БЫК.. = rl——- 1 — Т-1 (н)) (R’ — \ — dJ ‘ \ — 2dr cos’F) ‘1’ (2) из Формулы (o) вводится значение oxp, и после уменьшения 8
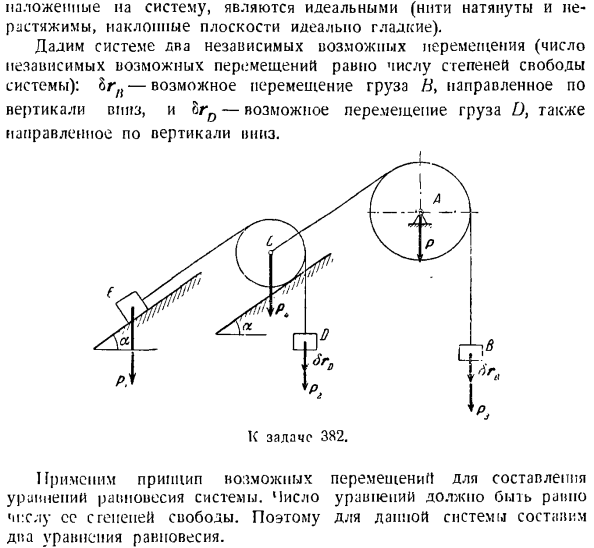
, а lrQ-возможное перемещение вертикальной нисходящей нагрузки D. Гол 382. Примените принцип возможных перемещений к редактированию Уравнение равновесия системы. Число уравнений должно быть равно Количество степеней freedom. So, в этой системе мы создаем 2 уравнения равновесия. Для построения уравнения равновесия системы, соответствующего возможному смещению Ln,
когда возможное смещение равно нулю, то есть нагрузка B и ролик C остаются неподвижными, нагрузка D перемещается по вертикали<вверх, а нагрузка P перемещается ПА brD параллельно наклонной плоскости. Примените принцип возможного движения и получите следующее. П <$ рд-П \ БРД грех = о、 Откуда Это не первый раз, когда пара была замечена вместе. (1) Для создания каждого из уравнений равновесия системы
OrD равен нулю, то есть brD = 0.In добавление, нагрузка D и E Относительно роликов C они остаются неподвижными, груз B перемещает па bgv вертикально вниз, а ролик C веса D W E перемещает па bbn вверх параллельно наклонной плоскости. Принцип возможного перемещения заключается в следующем: а-п-п-п-п-п-п-п-п-п-п-Син а = о、 Откуда Р * =(Пи + р * + Пи) з \ п*. (2) Присвойте значение sin a выражению (2).Из Формулы (1) Находим искомое значение веса груза B, P3. Проблема 383.Составная балка ADy в опоре 3 состоит из: 2 балок AC и CD, Соединенных точкой c charriolio.
Вертикальная сила P,= 8 / π и P. 2 = 6w приложены к белку переменного тока, пучок CO — направленный против часовой стрелки момент T = A T•m силовой пары. Размеры показаны на рисунке. один. .4, B и D определяют силу опорной реактивной силы. Не обращайте внимания на вес балки. Решение. Составная балка ad-это система из 2 твердых луча АС и СД находятся в равновесии. При выполнении этой задачи статическим способом, жестуря, при необходимости, мысленно разрывают шар игры Су
и отбрасывают СУ, чтобы заменить действие брошенного луча i: по той же причине для удаленного луча описывают непропорциональное равновесие. Наконец, мы решаем систему уравнений равновесия, или; и для одного из лучей, определяем предмет спора pt klch. Это решение довольно громоздкое. иипр -!ui » 4 возможный принцип смешивания, из 1 уравнения, составленного правильно, можно определить произвольную интенсивность реакции поддержки. Это значительно упрощает решение з’Дани.
Особенно когда нужно определиться!»Только 1 сила поддержки реакции. Это утверждение объясняется последовательным и даже независимым определением опорных реакций (A, B и L) с использованием принципа возможного смещения. Это показано на рисунке. И набор силы Р, и какая-то сила в момент времени T. Чтобы определить силу опорной реакции RA, мысленно отбросьте опору A и компенсируйте отсутствие этой связи силой опорной реакции JxA. если r-радиус-вектор точки, то Lr-возможное движение точки, А dr-фактическое движение точки. point.
In при разложении оси декартовых координат вдоль единичного вектора возможной формой смещения является 8R = bx1-j-oyj-bzk. Где oh, 1y, oz-проекция возможного смещения точки bg на соответствующую ось в декартовых координатах. Фактическое смещение задается уравнением dr = dxi + dyj + dzk. Где DXY, ДЗ-это проекция фактического перемещения д-р точки На эти оси, ДХ =&ДТ> ды = ydt аппликации, ДЗ = 2dt. Фактическое смещение точки равно 1 от числа возможных смещений этой точки (для фиксированного соединения). В случае нестационарных связей (по-видимому, зависящих от времени связей) учитывается возможное перемещение точек в моментально остановленных связях (то есть фиксированное значение момента). account. In в этом случае действительное движение перестало быть частным случаем возможности.
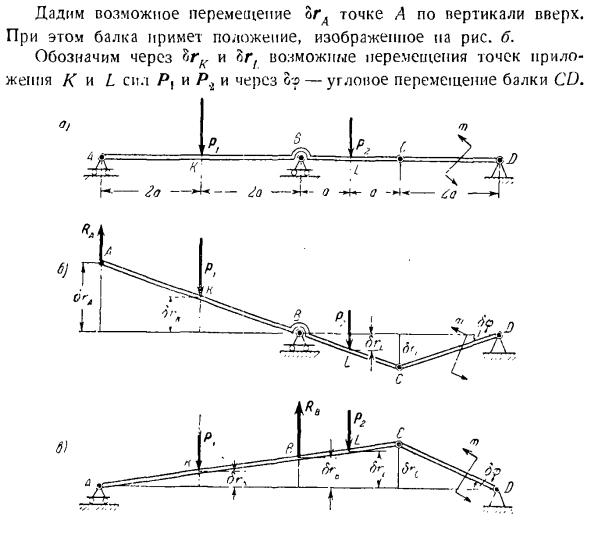
Приведем возможное смещение точки А в точку а в вертикальном направлении upwards. In в этом случае балка занимает положение, показанное на рисунке. б. bk и br {возможно смещение точек силы P и P K и L, и o? — Угловое смещение пучка компакт-диска. Архитектор К. 383. Используйте подобие треугольников, чтобы выразить связь между возможными смещениями линейного. БГА = 2og. = \ БР Д = 2ogs = 4Д & п. (1) Применяя принцип возможного смещения, уравняем сумму реактивной силы RA при работе всех заданных сил
и соответствующего возможного смещения до нуля. RAorA-t \ brK-r PjrL-r =0.(2) Используя выражение (I), после сокращения каждого члена в выражении (2) можно увидеть: После того, как номер заменен, он выглядит так: РА = 1.5 / Я Опорные реакции для определения прочности рН, ответы поддержите мысленно отбросить поддержка путем компенсации за потери соединения на прочность рублей. Дайте возможность перемещения шарнира вверх перпендикулярно шарниру C. In в этом случае балка занимает
положение, показанное на рисунке. с. через » oRA «% rt и 1pn обозначают возможные угловые перемещения сил P] t P2 P2 и точек приложения Rr K, L и B, а также возможные угловые перемещения балки CD и выражают взаимосвязь между ними. КУП = г реалов = Дж 8gd = 3Sr А. = 2а 5?。 (3) Применяя принцип возможного движения, пишем: — Prgrk-j-RBlrB-RlgL-mc =0.(4 )) После использования Формулы (3), сокращение на один член Формулы (4) на bc、 После того, как номер заменен, он выглядит так: /^.= 14,5 тонн
Осталось определить силу поддерживающей реакции. Примените принцип еще раз и освободите позвоночник или связь, а мысленно отбросьте опору I), компенсируя ее отсутствие силой реакции опоры RD. Приведем возможное смещение Ln, перпендикулярное точке D, upward. At в то же время, CD луч вращается! Угол pa против часовой стрелки ПГЧ Положение луча динамика не изменяется(см.
Рисунок D).Если записать принцип движения, то он будет выглядеть так: Ррфирн — \ — Мб?= 0.(си) Подставляя числа, используя редукцию каждого члена на brD в выражении (5) и выражении (6), можно увидеть: РП—2 / Вт. Знак минус указывает, что реакция поддержки (RQ) находится вертикально вниз. Задача 384.На нем изображена стремянка, а СВ. вмч.2 идентичные стороны stepladder. AC и CB остро связаны в точке C、 Концы A и B касательны к выступу пола. Вес
каждой стороны стремянки равен R. точка D имеет вес человека/ -. Определить силу реакции опоры в точке P, если AC = CB = 4CD, а CAB = L CBA = 6°. В Е С и Е. назначенными силами являются: Р-собака по обе стороны стремянки, Р \ — вес человека. Стремянка 2 /D с обеих сторон. указывает на ши. АК = КС = КЛ = л. Б = 2 СЛ)= Я Опора для определения силы реакции и вертикальной составляющей точки B R, придающей опоре B возможность перемещения vertically. To с этой целью
мы применяем принцип свободы от вяза, заменяя » выступ пола и точку B опорой на ролик, который может перемещаться вертикально (см. Рисунок L)». Я •БШ 1 Один L ’ 8, и 1- ’Г * 1′ / / 1А & совмещено: центр вращения оси вокруг неподвижной оси、 В точке B, одновременная вспышка cf. iv ПК;: КН! Папа:\ ч Если возможно, отметьте точку B, но по вертикали-Bi’cpx. In в этом случае правая Г10. 0п: совершает плоское движение по странице, а левая половина вращается вокруг оси а, которая перпендикулярна плоскости рисунка. направил возможное движение орка. Для точки C, перпендикулярной L C, найти положение мгновенного центра
вращения SB на стороне в точке A(в точке A перпендикуляры пересекают ore и og, {из точки C и B). Итак, в точке A Перетащите ступеньку на подвижную сторону лестницы, поверните- Мгновенный поворот Центра Шаг лестницы сбоку-КР, чтобы сделать плоское движение. Таким образом, вся стремянка получает возможное угловое смещение 89 вокруг точки А против часовой стрелки в плоскости фигуры. Применяем рассмотренный принцип
перемещения, то есть действие заданной силы и суммы вертикальных составляющих силы реакции Возможное перемещение точки приложения соответствует нулю.- P \ AM \ C-I, MSI&? — =(1) дано АМ = ACxos 60С= -£, а = в-1 ТС = АС, потому что ФИО * — Джей-потому что КД 60° ЛiV=Л7, » — / — TN = AC cos 60°+ 67. потому что»0 Мусаб = 2 /、 Если упростить уравнение (l), то получится: Опора в точке B обеспечивает горизонтальную подвижность опоры B для определения
горизонтальной составляющей Rm силы реакции. Для этого мы применяем принцип освобождения скрепления, заменяя выступ пола в точке в опорой на валик. Ролики можно перемещать горизонтально (см. Рисунок C). в точке B cooiBerci приложите усилие-реактивную силу Давайте дадим возможное смещение 8r / {точка B к горизонтали right. In в этом случае правая половина стремянки будет совершать плоское движение, а половина стремянки будет
вращаться вокруг точки А. возможное движение 8g перпендикулярно выступающему к точке с, определяет положение мгновенного центра вращения СВ стороны пересечения точек и точек, соответствующих из точки С и В. Следовательно, левая половина АС стремянки вращается вокруг точки А под углом 8°^ ^ по часовой стрелке, а правая половина АС стремянки вращается вокруг точки А под углом Определим зависимость между возможным угловым смещением и Shav. To для этого необходимо учитывать тот факт, что сустав с принадлежит обеим сторонам стремянки、 БГС = А Чо? D, 8gs =С Cr Cr. Так… = Авто + 3′> «>-
Таким образом, эта задача о равновесии твердой системы, состоящей из 2 половин переменного тока и Си лестницы переменного тока, была решена с использованием принципа возможного displacements. In в процессе решения задачи искомые компоненты силы реакции в точке B определялись независимо друг от друга из 1 уравнения.
Таким образом, вертикальная составляющая Rw силы реакции в точке B была найдена по формуле (I). Кроме того, горизонтальная составляющая R) Q найдена из Формулы(3). Чтобы решить эту задачу методом линии, необходимо создать 3 уравнения равновесия для всей стремянки, затем создать 3 уравнения равновесия для правой половины стремянки, а затем решить систему этих уравнений.
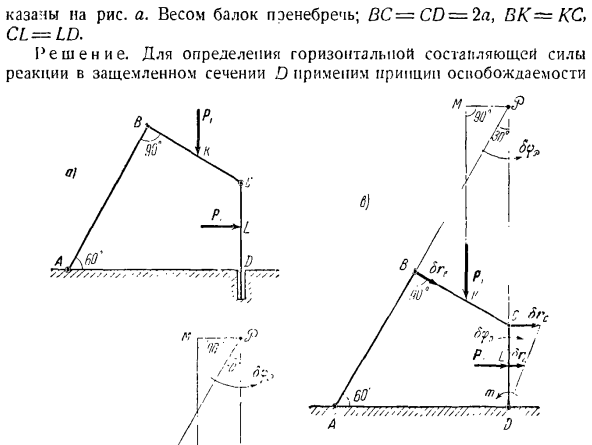
По сравнению с методом статики преимущества применения принципа возможного смещения к задаче равновесия системы твердых тел абсолютно неоспоримы. Задача 385.2 балки AB и BC dot/?Он соединен шарнирами. Луч BC зажат разделом D, который прикреплен на петлях к чистосердечному CD на конце C. крен AB зафиксирован с шарниром A на том основании с шарниром A. Определите горизонтальную составляющую силы реакции
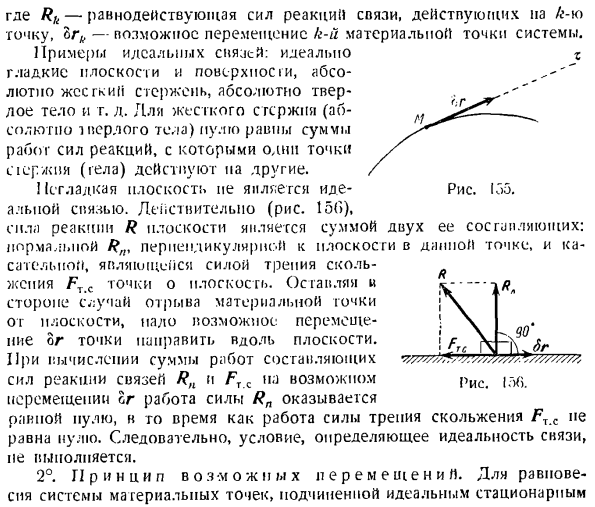
R0 и момент реакции rn зажимной части D. Мощность PL и Pi Рассмотрим массу точек на поверхности (рис. 154).можно двигаться с касательной плоскостью поверхности в заданной точке (конечно, направление движения точек в этой плоскости произвольно). Аналогично, если материальная точка находится
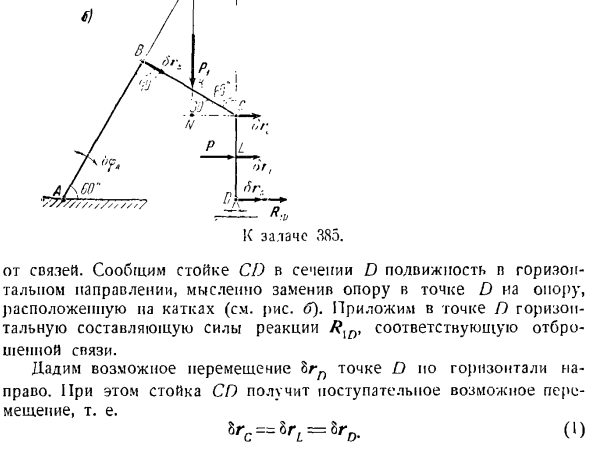
на кривой, то она представляет собой соединение, наложенное на точку (рис. 155), и возможные перемещения касательны к кривой в этой точке. Идеальное соединение. Идеальный 154. Связь называется, и сумма работы реактивной силы при возможном смещении точек системы равна нулю, то есть, к = \ Рис. котел а. вес балки игнорируется. BC-CD = 2at BK = KS, CL-LD. Решение. Как определить горизонтальную составляющую силы От соединения. Сообщите стойке CD в секции D о горизонтальной подвижности
и замените опору для точки D на опору в ролике (см. Рисунок B).в точке D примените горизонтальную составляющую силы реакции, соответствующую отброшенному соединению. Разберемся с возможным смещением Lp на точку D вправо по горизонтали side. In в этом случае стойка CD получит возможное поступательное движение. БФ = ВВС = bb0. (1) Луч АВ с возможностью углового перемещения<РД |и БГВ Он направлен перпендикулярно AB, то есть вдоль BC. При наличии возможного смещения балка BC совершает плоское движение. Центр момента вращения самолета и балки находится на пересечении перпендикуляров и восстанавливается
из точек B и C в точку L. И BFC. Поэтому луч БК вращается под углом против часовой стрелки вокруг мгновенного центра вращения. Применяя принцип возможных перемещений, вычисляют сумму работы заданных сил P и P *и горизонтальной составляющей силы реакции PlD при возможном смещении точек их приложения, равняясь ей нулю. (2) Pi I + P4brL + R [DZrD = 0. От треугольника и солнца: Я заметила. (4 )) И затем… После сокращения каждого члена в Формуле (1) на bn, с учетом формул(3), выполняется
следующее: Решая уравнение (4) на RU, можно увидеть: Знак минус указывает на то, что горизонтальная составляющая силы реакции направлена горизонтально влево. Определите величину недопустимого момента m зажимной части L). для этого замените зажим секции П неподвижным цилиндрическим шарниром и приложите момент реакции m в направлении против часовой стрелки (см. Рисунок B). Дает 8 возможных угловых перемещений: P0 к окружающей стойке CD Шарнир D вращается по часовой стрелке. Укажите возможные смещения в 8-й и 8-й точках B
и C соответственно, как и раньше、 Мгновенное положение центра вращения и Луча. Если возможное угловое смещение L0 данного CD находится вокруг точки D, то луч BC вращается на угол 8-p^в направлении против часовой стрелки вокруг мгновенного центра вращения^. Применяем принцип возможного смещения и получаем следующее. (6) 2а Один Пи \ м& \ БК + П! ЛД | мл? Д = 0. Рассмотреть возможные движения точки в до н. э., принадлежащий к балке
до н. э. и стойки для CD, в то же время, чтобы установить отношения. БГС = БГС = диски? КОМПАКТ-ДИСК Так что tPCg * = CD from = ’ Hack how тогда = 8p0 = <b0.Уравнение (6) после сокращения Терма не принимает следующий вид: КОМПАКТ-ДИСК I Pt I-f-Rf — / 72 = 0 Учитывая формулу(5), получим:
.»Р».Печень юковского. Применение аналитических методов для решения задачи равновесия плоского многозвенного механизма с использованием принципа возможных перемещений связано с вычислительными трудностями. Эти трудности возникают при составлении зависимостей между координатами точек приложения указанной силы. Вычисление вариаций этих координат, определяющих возможные смещения соответствующих точек системы, приводит к дальнейшему усложнению расчетов (например, см. Решение задачи 381, где рассматривается относительно простой механизм качания). В 1912 году И. Е. Жуковский предложил метод
графового анализа для решения задачи равновесия плоского многозвенного механизма под названием»Жуковский рычаг«.Методы решения задач основаны на принципе возможной скорости. Так как скорость точки системы в действительном движении имеет направление drbt, а в стационарной связи действительное перемещение равно 1 из возможных, то конкретная формулировка принципа возможного перемещения может быть дана путем замены
возможного перемещения b ^на «возможную скорость» — величину, пропорциональную действительной скорости^^. Принцип возможной скорости в случае равновесия системы материальных точек задается формулой k = I Или северный^^ X FkVn C0S (Fk> К-и Где Fu-заданная сила, приложенная к точке k — \системы,<ok-возможная скорость этой точки. Все соединения, применяемые к системе, являются идеальными и фиксированными. Удобство использования рычага Жуковского при решении задачи равновесия плоского
многозвенного механизма заключается в том, что силы реакции идеальной муфты не входят в уравнение равновесия. После решения уравнения равновесия можно определить одну из заданных сил (движущую силу, полезное сопротивление, вредное сопротивление и т.).С использованием рычагов Жуковского даже изучение равновесия сложных механизмов не доставляет хлопот. Недостатком рычагов Жуковского является то, что они должны повторять структуру для каждого положения механизма. Решение задачи с «Жуковским рычагом» рекомендуется проводить в следующем
порядке: 1) нарисуйте схему механизма в положении задачи. 2) укажите силу, установленную на чертеже. З) установите скорость 1 из точек механизма и создайте индикатор скорости конкретного положения механизма. 4) спидометр прикладывает определенную силу на изображении, в конце соответствуя вектора скорости на тех применении points. In в этом случае все установленные усилия должны быть повернуты на 90 градусов по часовой стрелке или против часовой стрелки. 5) скоростной план представлен в виде инвариантной формы, в которой имеется неподвижная точка
на полюсе, то есть рычаг с точкой опоры скоростного плана и полюсом. Запишите уравнения равновесия рычагов, то есть сумму моментов относительно полюсов спидометра картины всех заданных сил, вращавшихся в 90-е годы, равную нулю. Это уравнение равновесия «Жуковского рычага» является также уравнением равновесия этого механизма. 6) после решения полученного уравнения равновесия определите величину искомого набора сил. Задача 386.Показаны сочлененные 4-линковые автономные адресны
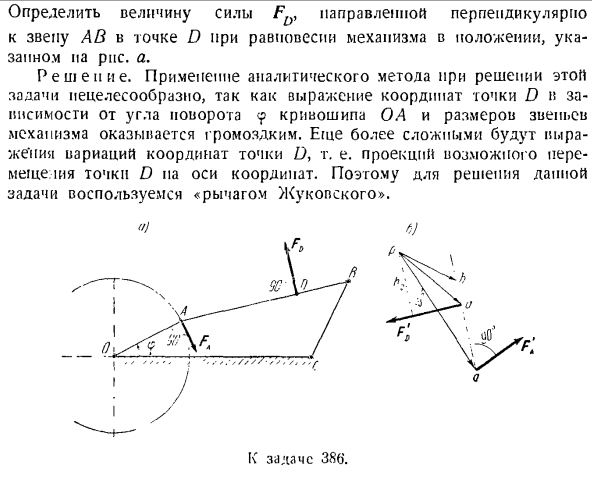
книги. Усилие FA приложено к соединению a перпендикулярно кривошипу OA. Рис. Д. Решение. Применение аналитических методов для решения этой задачи нецелесообразно. Это объясняется тем, что выражение координат точки D, зависящее от величины угла поворота<p и звена механизма кривошипа ОА, является громоздким. Более сложным является представление изменения координат точки D, то есть проекция возможного движения точки D вдоль координатных осей. Поэтому для решения этой задачи используйте
«Жуковский рычаг». Шесть)) Голов 386. !5a схема механизма (см. рисунок а) показывает заданную силу FA И Fd. Сделайте указатель скорости, соответствующий положению рассматриваемого механизма. Повернем а к скорости вращения по часовой стрелке направление вращения кривошипа ОА<к шламу (коэффициент скорости выбирается произвольно, а направление скорости может быть изменено в обратную сторону).Как только полюс p будет выбран вне диаграммы механизма, постройте вектор скорости vA =
pa и допустимую шкалу скорости (см. Рисунок 6). Скорость точки и должна быть направлена перпендикулярно звену самолета, кружащему вокруг точки С. проведите вспомогательную линию перпендикулярно самолету к полюсу р. Вектор скорости точки B находится на этой прямой, и чтобы определить положение конца<vn, проведите линию через точку A перпендикулярно AB. АБ)… ВН = ЗПБ. На прямой ab помещается конец вектора скорости точки звена A B.
Где результатом Связной реактивной силы, действующей на N-ю точку, bk является возможное движение N-й материальной точки системы. Идеальный пример соединения: совершенно ровные плоскость и поверхность, абсолютная твердая штанга, абсолютное твердое тело и так далее on. In в случае жесткого стержня (абсолютно твердого) пуля будет равна сумме действий реактивных сил, с которыми одна точка сжатия (тело) воздействует на другую.
Негладкая плоскость не является идеальной. 155. Альпийская связь. Наверняка(рис. 150)、 Плоская реактивная сила R представляет собой сумму ее 2 составляющих. Касательная, представляющая собой Нормаль R, перпендикуляр r к плоскости в данной точке и силу трения скольжения точки на плоскости, FJC. Кроме отделения материальной точки от плоскости, возможные точки должны быть перемещены вдоль плоскости. При вычислении суммы работы составляющих сил реакции Rn и Frc в сочетании с возможными перемещениями, либо работа силы Rn оказывается равной пуле,
но работа силы трения скольжения F1C не равна нулю. Поэтому условия, определяющие идеальность общения, не выполняются. 2°.Принцип возможного движения. О равновесии системы материальных точек, подчиненных идеальной стационарной Реклама Р Из пропорций:= -.Соедините полюс p с точкой a, чтобы определить скорость точки D. ВД = др. Здесь, в точках a и d, применяются указанные силы FA и Fd. Например, вращайте их по часовой стрелке, вращая их в одном направлении под углом 90°.Вращаемая сила представлена F’A и F’N (поскольку
направления GA инаправляет F’N перпендикулярно ab, потому что оно перпендикулярно AB). Представим себе карту скоростей с неподвижной точкой на полюсе p, то есть неизменной фигурой PID в виде рычага с опорой на точку p. под действием силы F’a запишем уравнение равновесия этого рычага ’Ф°’ Мп (ФА) — \ — Мп (фр)= 0、 То есть F \ \ pa | — p’Dhn = 0, где 1> 0-перпендикуляры,
опущенные с полюсов рабочей линии pp F ’[y мы имеем: Г’п= ^ F’ y, т. е. Fn = = R na измеренная длина 6 сегментов (pa и hf) и их определение Найти коэффициент, искомое значение системы Fn. Если вы измените положение механизма, структура должна повториться.」 Задача 387.Многозвенная артикуляция рисует плоско!! Кривошипно-шатунный механизм приводится в движение силой F t, приложенной к хомуту a перпендикулярно оси OA. При вращении
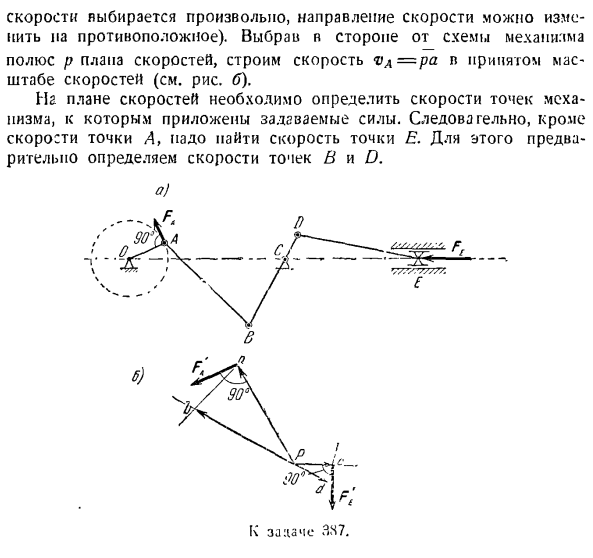
кривошипа ОА звено BD вибрирует вокруг неподвижной оси С и приводит в движение привод через стержень DB; — g в полном размахе-ползунное колесо перемещается/:.Полезное сопротивление FP горизонтальной силе, приложенной к ползунку. Определим величину силы FE при равновесии механизма в положении, указанном на рисунке. один. Решение. Равновесие такого механизма не следует изучать аналитически, принимая во внимание неизбежные трудности расчетов. Для решения этой задачи используйте
«Жуковский рычаг«.Схема механизма (см. рисунок а) показывает заданные силы FA и Гп. Сделайте указатель скорости, соответствующий положению рассматриваемого механизма. Дайте скорости Vа точки А и F против ОА кривошипа. направление t, то есть против часовой стрелки перпендикулярно (модуль Скорость выбирается произвольно, а направление скорости может быть изменено в противоположную сторону).Отдельно от схемы механизма выберите полюс индикатора скорости p и постройте скорость<vA = pa на разрешенной шкале скоростей (см. Рисунок B). На чертеже спидометра необходимо определить скорость точек
механизма, на которые действует данная сила applied. So, помимо скорости точки А, нужно найти скорость точки Б. Для этого сначала определяется скорость точек В и D. один) Правое и правое направление скорости точки B перпендикулярно звену VO и висит вокруг оси оси C. Пройдите прямую линию через точку a, тройку AB, запах, точку b на пересечении этих линий(конец вектора скорости точки B) 1.3 скоростной план pb = pa ab).Поэтому скорость точки h D легко определить, так как VB и vn параллельны и ориентированы в разных направлениях. отложите, по прямой линии, проведенной
в противоположном направлении вдоль ПБ Сегмент ПД. Значение вычисляется из percentage=. Итак, vD = pd. It остается найти скорость точки L\, которая направлена горизонтально. Нарисуйте горизонтальную линию на полюсе p. затем, через точку d, укажите вспомогательную линию, перпендикулярную звену DE. Ссылка DE-это пересечение с горизонтальной линией Положение точки e (v£= vD Pa ПЭ = = ПД-Джей-Ди. Так, в [: = пе. Указанные силы FD и F£приложены к точкам A и E механизма. Для решения задачи с помощью
«Жуковского рычага» эти силы подчиняются и предварительно поворачивают их на 90°в одном направлении, прикладывая к концам вектора скорости и плоскости скорости<vE. At в точке а, являющейся ребром<ол, прикладывают силу F’V, которая получается вращением силы FA против часовой стрелки (FA перпендикулярна ОА, F’a параллельна ОА, F’a перпендикулярна ПА). в точке с, конечной точке, прикладывают силу F’F для получения се ния
отношение pa к re является единичным и простым, поскольку оно определяет длину этих сегментов. с. При изменении положения механизма повторите все конструкции. Для соединения необходимо и достаточно, чтобы сумма работы данной силы при каждом возможном смещении точки системы была равна пуле: я] fv8r * = 0. фут-1 Аналогично, в проекции на ось декартовых координат имеются: 2+ -!- БМ)= О-Ч-1 Преимущество принципа возможного смещения состоит в том, что формулировка силы реакции идеальной муфты не ясна. Принцип возможного перемещения широко применяется
к меховым пикам. С его помощью можно очень легко выявить проблему равновесия твердого тела и твердой системы, а также определить взаимосвязь между указанными значениями forces. It особенно эффективно применять принцип возможных перемещений при решении задачи равновесия твердых систем. На основе рассмотренного принципа смещения можно вывести
уравнения равновесия твердых тел при наличии как плоской системы сил, так и пространственной системы. Если все соединения, наложенные на систему, не идеальны, например, если имеются негладкие опорные поверхности и поверхности, то к заданной силе следует добавить силу трения, а следовательно, и не только заданную силу, но и движение системы point. In в случае сил трения составленное уравнение определяет соотношение между заданными силами. если необходимо определить силу реакции идеальной связи jR-br = 0, то, применяя принцип свободы от связи, она отбрасывает соответствующую связь и заменяет ее желаемой силой реакции. При создании уравнения равновесия необходимо прибавить силу этой реакции сцепления к заданной силе. Этот метод решения задачи
равновесия в твердой системе очень эффективен, так как искомая интенсивность реакции связи определяется непосредственно из составленных уравнений равновесия. (Применяя обычный статический метод, мы должны построить систему уравнений равновесия и определить искомую интенсивность реакции связи в результате решения этой системы уравнений.) Рекомендуется решать задачу равновесия твердых и твердотельных систем,
используя принцип возможности решения задач в следующем порядке: 1) изобразите его! На рисунке показана мощность набора; 2}Если у вас есть соединение в день оплаты, добавьте соответствующую силу реакции соединения (например, силу трения). 3) при необходимости определить силу реакции связывания, мысленно отбросить соответствующую связь и заменить ее желаемой силой реакции связывания (в случае # 0). В зависимости от того, имеет ли система 1 степень свободы или несколько степеней свободы, должны быть выполнены дальнейшие действия. а) R-случай системы
с 1 степенью свободы: 4) дает 1 возможное движение точки внутри системы и выражает возможное движение точки приложения силы в ответ на данное возможное движение. 5) вычислить сумму всех сил работы, указанных в пунктах 1), 2)и 3) вычислить соответствующие возможные перемещения па их приложенных точек и сделать эту сумму равной пуле. (i) после решения подготовленного уравнения равновесия определите целевое значение. 6) для систем с некоторыми степенями свободы: 4) выбрать независимое возможное смещение точек системы, число которых равно числу степеней свободы этой системы. 5) придание возможного смещения, соответствующего
1 из степеней свободы системы, при одновременном рассмотрении возможных смещений, соответствующих остальным степеням свободы, равным нулю. Через это возможное смещение выражается возможное смещение точки действия силы. б) вычислить сумму всех действующих сил, указанных в пунктах 1), 2)и 3) вычислить ПА соответствующих возможных перемещений их прикладываемых точек и сделать эту сумму равной пуле. 7) вычислить для каждого из возможных перемещений, которые являются независимыми5) и 6) выполнить в ряд и сформировать систему уравнений равновесия
с числом, равным числу независимых возможных перемещений, то есть числу степеней свободы в системе. 8) после решения системы, состоящей из уравнений равновесия, определите искомое значение. Проблема 377.На рисунке показана плинтусная система, используемая для подъема груза K>, подвешенного к нижнему рычагу в точке D. подъем осуществляется силой F, которая направлена вертикально вверх и приложена к точке B верхнего рычага. Идентифицировать Вес поднятого груза K>.Если G= 10 кг, а -^ — = 10 (см.
Рисунок). Решение. При решении этой задачи статическим способом необходимо применять принцип невосприимчивости связи, мысленно нарушая тягу переменного тока, заменяя действие рычага соответствующей силой реакции связи, и отдельно рассматривая равновесие верхнего и нижнего рычагов. После исключения реактивной силы тягового усилия переменного тока из уравнения равновесия можно определить вес P поднятого груза K.
Смотрите также:
Предмет теоретическая механика
| Метод кинетостатики | Общее управление динамики системы материальных точек |
| Давление вращающегося твердого тела на ось вращения | Уравнение Лангранжа второго рода |

