Оглавление:



Принцип Сен-Венана и гипотеза плоских сечений
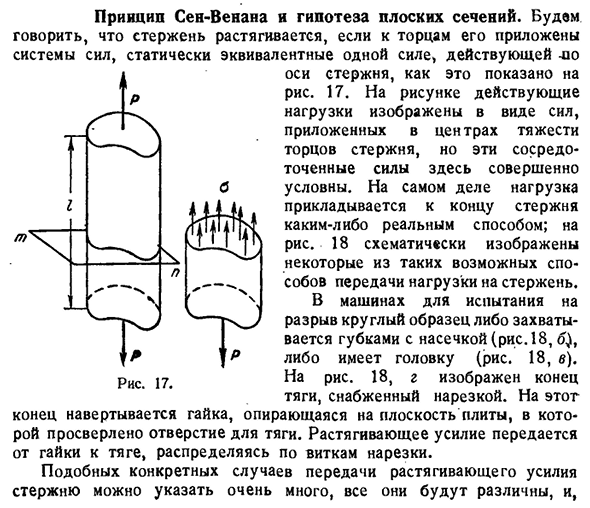
- Принцип солнца-Венанта и гипотеза плоского сечения. Как показано на рисунке, это говорит о том, что стержень растягивается, когда его конец прикладывается к системе статически эквивалентных сил к одной силе, действующей на ось стержня. 17.
На рисунке рабочая нагрузка изображена в виде силы, приложенной к центру тяжести на конце стержня, но концентрация этих сил полностью условна. На практике нагрузка прикладывается к концу стержня несколькими реальными способами. Схематически показаны некоторые из этих возможных
способов передачи нагрузки на 18 стержней. Людмила Фирмаль
Тестер на растяжение захватывает круглый образец с зубчатой губкой(рис. 18, б), или имеющие голову(фиг. 18, В нет. Для риса. 18, g показывает конец стержня с разрезом. Для этого гайку завинчивают и помещают на плоскость пластины, в которой просверливают отверстия для тяги. Тяговое усилие передается от распределенной гайки по ходу вращения разреза на стержень.
Частных случаев передачи растягивающей силы на такие стержни можно указать очень много, все они различны, и при изучении всех их по отдельности, при расчете растягивающих стержней, все усилия прикладываются к каждому концу стержня, не учитывая индивидуальных особенностей, в зависимости от конкретного способа приложения нагрузки, при этом он руководствуется правилом, называемым принципом Сен-венина, названным в честь французского ученого (1797-1886), давшего ему такое решение Он назвал его, сформулировал принцип, применимый не только к растяжению сжатия, но и к скручиванию материала, изгибу и многим другим проблемам сопротивления и теории упругости.
- Формулировка этого принципа в его применении к рассматриваемой проблеме. Способ приложения силы к концу стержня действует только в непосредственной близости от конца. Несколько расплывчатая формулировка (непонятно, что означает «непосредственная близость»), многочисленные эксперименты и теоретические исследования показали, что этот принцип не является строго доказанным положением в наиболее распространенных случаях, так как расстояние от края напряжения, связанное с неравномерным распределением края, т. е. так называемого напряжения, всегда обнаруживают очень быстрое затухание, на практике же эти локальные напряжения становятся незаметными вдали от края порядка латерального размера.
С тонкостенным стержнем дело может обстоять иначе (см. главу IX, 109-ю и XI). Это означает, что для всех изображений на рисунке. В 18 случаях напряженное состояние отличается только в незатененной части. Напряженное состояние части стержня, снятой с конца (заштрихованной на рисунке), во всех случаях является одним и тем же состоянием простого натяжения, и напряжение всех точек одинаково, а область, близкая к месту приложения силы, является областью локального напряжения, а следовательно, особой работы. Согласно принципу Сан-бенанта, » напряженное состояние центральной части стержня не зависит от
способа приложения силы, поэтому оно совпадает с простейшим случаем, показанным на рисунке. 11. Людмила Фирмаль
при равномерном распределении нагрузки параллельно оси стержень прикладывается к торцам. Это напряженное состояние является однородным и одинаково параллельным оси стержня во всех точках поперечного сечения напряжения. Каждый элемент объема деформируется точно так же, как и конец, как показано на рисунке. 11 призмы двигаются, но остаются плоскими и параллельными друг другу после приложения нагрузки. Этот факт-сохранение плоских сечений под напряжением-иногда кладется в основу всей теории, так как основная гипотеза плоских сечений производится следующим образом: Разумеется, плоской остается только часть, удаленная от места приложения силы на расстояние не менее порядка ее бокового размера.
Все вышесказанное относится и к случаю сжатия, который отличается от случая растяжения только формальным изменением направления силы. Реальная разница между растяжением и сжатием гораздо глубже, поскольку при сжатии могут возникать новые явления, приводящие к потере устойчивости. Центральный сжатый прямой стержень, длина которого намного больше поперечного размера, фактически неизбежен при небольшом эксцентриситете силы, удерживающей форму прямой линии, или небольшой кривизне оси стержня, только когда сила сжатия меньше определенного критического значения, но сила сжатия не так важна, но она также вызывает изгиб без сжатия только. В этом случае эффект изгиба часто намного больше, чем эффект сжатия. Эту ситуацию необходимо учитывать при расчете сжатого стержня, ей будет посвящена одна из глав нашего курса. Здесь нет принципиальной разницы между растяжением и сжатием.
Смотрите также:
| Тела изотропные и анизотропные | Напряжения и деформации при растяжении |
| Стержни и стержневые системы | Расчеты на прочность при растяжении и сжатии |

