Оглавление:





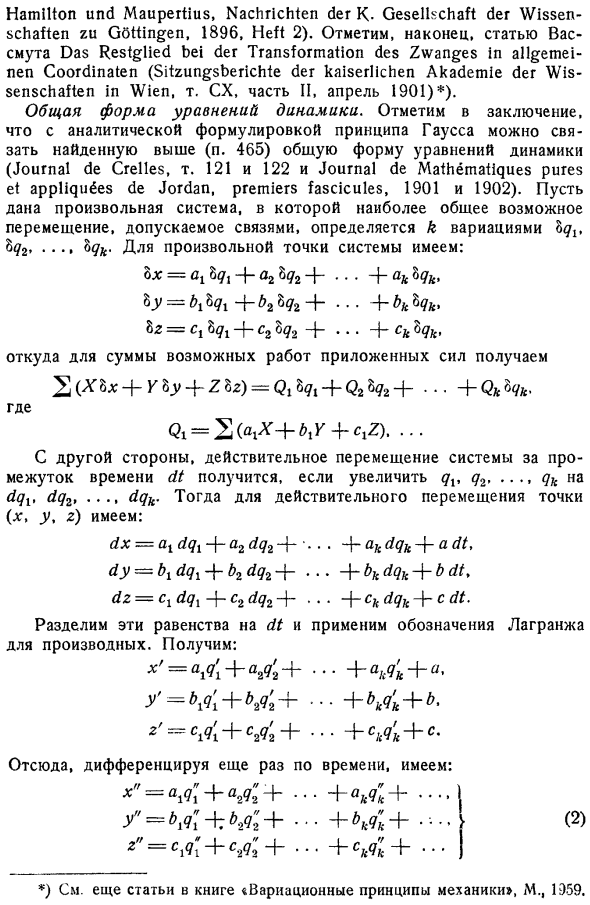


Принцип наименьшего принуждения Гаусса. Формулировка принципа
- Ученые искали различные способы свести уравнение движения к единому началу путем введения интегралов или функций, которые минимизируются относительно фактического движения системы по сравнению с возможным близким движением. Эта идея выражена главным образом в принципе минимальных действий пункт 486.Затем следует более общий принцип Гамильтона 483. Из этого принципа очень легко вывести уравнение Лагранжа голономной системы, но в случае неголономных систем эти аргументы и выводы уже неверны. Мы имеем дело с принципом минимального принуждения Гаусса. Этот принцип является наиболее распространенным и не вызывает проблем с его применением.
Преимущество этого принципа заключается в том, что он имеет простую аналитическую формулу, которая позволяет свести определение кинетического уравнения любой системы к голономному и неголономному, чтобы найти минимум функции 2 го порядка. Вот начальный перевод статьи Гаусса и Приложение I. комментарий Бертрана X vol. II, с. 357 воспроизвести. В Томе 4 журнала clerses Гаусс опубликовал прекрасную теорему, содержащую общие законы равновесия и движения. Очевидно, самое изящное выражение дано им. Читатели Франции будут благодарны нам, если мы приведем здесь перевод нескольких страниц, посвященных знаменитой геометрии, которая объясняет этот новый принцип.
Сила, вызывающая движение планеты вокруг Солнца, зависит только от расстояния, и она, по-видимому, вынуждает точку ее приложения описывать замкнутую кривую. Людмила Фирмаль
Как известно, по принципу виртуальной скорости статические задачи превращаются в чисто математические задачи Цитаты из русской версии LaGrange, analytical mechanics, Volume II, V. S. Goffman, G. N. Reporting by Doina Chiacu Editing by David Gregorio см. 411, State Technical Publishing House, 1950. Примечание, транс Принцип динамики Даррена Бейла меняется на статический.
Таким образом, один основной принцип равновесия или движения существенно не отличается от вышеупомянутых 2 принципов, и каким бы ни был этот основной принцип, его всегда можно рассматривать как более или менее прямой вывод из упомянутых 2 принципов. Поэтому это не означает, что новая теорема не заслуживает внимания. Напротив, всегда интересно и познавательно изучать законы природы с новой точки зрения, будь то для достижения более простой интерпретации конкретной проблемы или для достижения только более точной формулировки.
Великий геометр Лагранжиан, который очень много обосновал науку о движении на основе принципа виртуальной скорости, не упустил возможности усовершенствовать и обобщить принцип движения. mopelte. It речь идет о самом маленьком действии. И, как известно, этот принцип во многих случаях имеет огромное преимущество перед геометрией. Суть принципа виртуальной скорости заключается в том, что, так сказать, этот принцип является общей формулой, решающей задачу статики, и поэтому он может заменить другие принципы. Но он не несет никаких признаков абсолютного доказательства того, что вы будете убеждены, как только привыкнете к его представлению.
С этой точки зрения, основная теорема, которую я пытаюсь Она представляется мне приоритетной более того, она имеет то преимущество, что может одновременно охватывать общие проблемы равновесия и движения. С другой стороны, если кажется более удобным для развития науки и индивидуального исследования перейти от простого к более сложному и от простого закона к более сложному, то нашему уму необходимо обратное движение, чтобы достичь более высокой точки зрения, потому что вся статика представляется ему как частный случай динамики…
Новые принципы включают в себя: Движение системы произвольно связанных и затронутых материальных точек происходит в каждый момент, когда все эти точки свободны, так как принуждение, применяемое между ними и возможным, совершенно совпадает с ним. Э, это было бы бесплатно. т, т, т,… Масса точек а, а, а, а,… Каждая позиция во времени t б, б, б,… Места, где они заняли бы после бесконечно короткого периода dt, приобретенные ими в начале этого периода под влиянием силы и скорости, действующих на них.
Вышеприведенный принцип гласит, что позиции C, c , c , занимаемые этими пунктами, входят в число всех положений, допускаемых наложенными на них облигациями, и что сумма является суммой mbc2 4 t b s 2 + t b s 2 + … Минимальное значение. Равновесие это частный случай общего закона. Возникает, когда нет скорости и итога для точки n + t AI 2 + tpa 17 2 + … Если минимум или, другими словами, система удерживается в статическом состоянии, то соединение оказывается ближе к свободному перемещению всех точек системы в случае удаления соединения, чем движение, которое могло быть разрешено.
Доказательство. В момент времени t точка м занимает положение с координатами x, y и Z. Она имеет скорость, равную 1 го порядка производной X, у, Z, чьи проекции о времени х, г, р, а проекция которой равна 2 ой производной от X. г, з Из координат x, y, z времени наконец, в дополнение к реакции ограничения на нее действует данная сила, и результатом является проекция X, Y, Z. In фактическое движение системы, координаты x, y, z являются функциями времени. t m занимает позицию a и занимает позицию c в момент t dt. Согласно формуле Тейлора, если вы ограничиваете ее первыми 3 членами, координаты точки c равны х + х ДТ + х ДП. г г Гумбольдт + г, ДП.
Если во времени t точка m становится свободной, то есть если связь внезапно уменьшается, то эта точка называется фундаментальным законом механики С. 69, причем ускорение проекции должно быть равно положению b после интервала Время dt определяется по той же формуле, что и предыдущее one. In Формула, x , y , z должна быть заменена на количество Итак, для координат точки b x + x dt + dt2, y y dt + dt2, z + z dt + dP существует проекция в векторе cb КБ Кроме того, проекция вектора mcb, полученного умножением cb на массу, равна г ст2 х МХ, г к МУ ст2, ст2 з МЗ. Поэтому на основе общего уравнения динамики С х МХ 8х + у му 6й + з МЗ 8з = 0.
- То есть сумма работы вектора в формате mcb будет равна нулю для любых возможных перемещений, допускаемых ограничением. г, г,…Позиция с, С, с,…Точка m, m , m , которая расположена бесконечно близко и без разрыва связи системы….Вы также можете сделать снимок с помощью камеры. работа вектора МКБ по возможному движению Св Т КБ Су. Количество этих штук необходимо Си Су. Равны нулю во всех положениях y, y , y Но это понятно yb2 уу + КБ 2 = yy2 + в FB2 2си КБ. И так оно и есть. м Б2 = 2lm кб2 + 2lm РФ 2С СВ с. Потому что последняя сумма равна нулю м yb2 СВ2 = м cy2 Отсюда и разница 2 С с, с,…Случай Всегда положительный.
Точка y, y , y , y ,…Если совпадают только точки С, то они равны нулю. Итого 2t cP1 всегда является минимальным значением по мере необходимости. Аналитическая формулировка принципа Гаусса.
Ту же теорему можно выразить в следующем виде: кинетический момент системы относительно точки о равен всей массе в предположении, что она сосредоточена в центре тяжести. Людмила Фирмаль
Исходя из приведенной выше формулы для проекции вектора cb, она выглядит следующим образом: В другом движении, которое допускают облигации, точкой того же периода dt является позиция m, y,….Если ускорение достигнуто, другими значениями являются x, y и r .Для облигаций, вы найдете также Потому что 2m bcr всегда меньше, чем 2 m T2.Тогда вы можете сказать Из всех ускорений, вызванных сцеплением, фактическое ускорение x , y , r в каждый момент времени t Различные точки в системе будут точками для обеспечения минимальной функциональности х, г, г,…2 го числа Это аналитическая формулировка принципа Гаусса. А. из Лейпцига.
Майер заимствует следующую историко библиографическую информацию: аналитическая формулировка принципа Гаусса была упомянута Якоби в 1 из неопубликованных лекций. Независимо от Якоби, оно было дано компании Schaeffler Шеффлер, третья группа derbmir hichen З. С. С. 197.Он был воспроизведен компанией Mach Лейпциг, умереть механик Лейпциг, 1883, Герц gesammerte Верке, Иллинойс и Больцмана Лейпциг текстильных умереть Принсипи дер мечник, Лейпциг, 1897.
Это было очень давно.1 Уиллард Гиббс, основное уравнение динамики, американский журнал математики, Том II, 1879 в своей работе Уиллард Гиббс проиллюстрировал применение этой аналитической формулировки к различным проблемам, особенно к проблеме вращения твердого тела. Наконец, Мейер использовал эту фразу в интересной статье, озаглавленной Beibenchengen s Beeung der Aufstellung der Bewegung der Bewegung Rebeungslose Punktsysteme, beingungsungleichungen untcrworfen sind und zur Regulierung der Stbsse. physikalischen классе дер kbnigl. Сакс. Гезельшафт дер wissenschaften ЗУ Лейпциг. Sitzung vom 3 Jul 1889.
Вы также можете обратиться к статье Helder со сравнением различных принципов NoeIder, Ueber die Principien von Гамильтон и мауперти, K Gesellschaft der Wissen schaften zu Gottingen, 1896, Heft 2.Наконец, реконструкция бактоломед цвангских метаморфоз в Вене, Wis senschaften Kasenlichen Akademie der Kaiserlichen Akademie der Wien, vol. Обратите внимание на статью СХ, Часть II, 1901 4. Общая форма уравнения dynamics. In заключение следует отметить, что аналитическая формулировка принципа Гаусса позволяет связать общую форму уравнений вышеуказанной динамики стр.
Наиболее распространенными возможными перемещениями, допускаемыми муфтой, являются изменения K 8ur 8y2….. дайте любую систему, определенную adk. Для любой точки в системе существуют: 8х = fl1891H А28 2 + … + akZqk, 8У = 18 1 4 f 26 24… 4 ifc8 сказал он. 82 = c, 8, + cs 8 2… 4 ck bqk Для суммы возможных эффектов приложенных сил S 5 8×4 f, 83 4 28z = Ql8g 4 Q2 8 24 4 Q 4 Куда Ци = С. АИ 4 Ф ху 4 CjZ. Увеличение q, q2, с другой стороны, оборачивается фактическим движением системы за временной интервал dt.
Затем, чтобы на самом деле переместить точки x, y, z есть следующие: ДХ aldql a2dq2… akdqk АДТ, ды Би dqi 4 Б2 dq2 4… 4 БК dqk 4 Б, ДТ, ДЗ = Cidqi c2dq2… Джей СК dqk Джей с ДТ. Разделите эти уравнения на dt и примените к производным нотацию Лагранжа. Что взять х = Ми4 О2 4 4 М 4. = М14 4 4 М14. 2 = ки 4 ка 4 М 4 х Итак, если мы снова дифференцируемся во времени, мы получим следующее: =ми4 mJ4 4 МИ4 я 4 Мг4 + У4 4 2 = s19 4 Ma 4 4 M 4 1 2, М. 1959. См. также статью в книге вариационные принципы механики Подставляя значение 2 в сумму, представленную R 1, сумма q , q … это будет 2 я функция относительно в qk.
Возможное ускорение, основанное на Формуле 2 Точки x, y, z определяются различными значениями: q , g .. благодаря дь. Значение равно q , q … дь если уравнять частную производную суммы R к нулю относительно q, то получится значение, соответствующее действительному движению. вопрос.. вопрос к Это связано с тем, что фактическое ускорение точки минимизирует сумму R. запишем эту сумму. Р ИС я + Г Л Я 2 а с J = + ий + Ж + 3 Здесь неписаные термины не зависят от x, y и Z. S = I S Y = 7 2 + Z + Система ускоренной энергетики. Между тем, сформируйте сумму 2 х + о + зз. Если в нем вы заменили его на x , y и значение 2, то эта сумма будет в виде: Пр + + Qk4k Не Q членов, вопрос. дь не пишет.
Сейчас… Чтобы получить уравнение движения, q, q это о частной производной…. q k должно быть равно нулю = С. .. Qkqk. Таким образом, мы получаем уравнения, оцененные в 465, DR,= o. рр,=……….Д а=о о 1 oqi oqk Это справедливо для всех систем связи и параметров. Энергия ускорения s это функция, характеризующая систему. Объем Q Q2….
Смотрите также:
Теоретическая механика — задачи с решением и примерами
Если вам потребуется заказать теоретическую механику вы всегда можете написать мне в whatsapp.

