Оглавление:




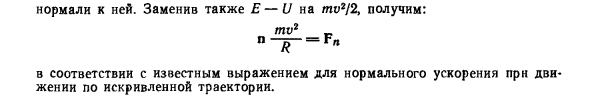

Принцип Мопертюи в физике
- Принцип Мопеля Дважды. Принцип минимального действия — движение машины Система полностью определена. Решая уравнение движения, которое следует этому принципу, Зависимость орбиты мю и положения на орбите Время. Ограничьте себя более узкими вопросами определения Оказывается, для этой цели может быть установлена только сама траектория (кроме временной части задачи).
Упрощенная форма принципа минимального действия. Функция Лагранжа и ее функция Гамильтон явно не включает время, поэтому энергия системы сохраняется. H (p, q) = E = const Согласно принципу минимального действия, изменение в действии для данного начального и конечного значения координат и времени (таких как to и t) равно нулю.
с фиксированными начальными и конечными координатами Людмила Фирмаль
Предыдущий случай Чтобы разрешить изменение конечного момента времени t , Да (ср. (43,7)): bS = -Hbt. (44,1) Здесь вместо сравнения всех виртуальных движений системы сравниваются только те, которые удовлетворяют закону сохранения энергии.
Для таких орбит вы можете заменить H на (44.1) Константа Е bS + Ebt = 0. (44,2) Описывая действие в форме (43.8) и заменяя H на E, S = J 5P2i d q i-E (t-to). (44,3) Первый член в этом выражении So = J 52Pidqi (44,4) Также называется сокращенным действием.
- Назначить (44,3) (44.2), найти bS0 = 0. (44.5) Следовательно, минимальное значение укорачивающего действия Присоединяйся ко всем траекториям, которые соответствуют закону сохранения энергии и проходи конечную точку в любое время. Чтобы использовать такой вариационный принцип, сначала выразите импульс, и весь интеграл (44.4) Через координату q и ее производную dq.
Для этого Следует использовать равенство p ’= W, L (« ’l)» (44’6) Представляет собой уравнение определения импульса и закон сохранения энергии E {q, f) = E (44,7) Выразите производную dt из последнего уравнения по координате q и их производной dq и подставьте их в уравнение (44.6) Выразите импульс с помощью d dq и энергии E u u Он играет роль параметра.
Этот принцип обычно называют принципом Морпертуи Людмила Фирмаль
Полученный таким образом принцип вариации определяет траекторию системы. (хотя его точная формулировка была дана Эйлером и Лагранжем).
Явно выполнить указанное действие для нормального Форма функции Лагранжа (5.5) как отличие от динамики Потенциальная энергия: L = 1 ^ 2 aik (q) qiqk к U (q). И энергия E = \ ^ 2, aik (q) qiqk + U (q). Я, к Из последнего равенства dt = \ / E2a (Ei) k (448) И эта формула dqi = ^ 2 aik ~ ^ -dqi, Я, к Найти сокращенное действие в форме Итак, = [// 2 (—U) к, ккdqi dqk. (44,9) J i, k
Особенно по одному важному вопросу, кинетической теории энергии rp _ t (дл \ 2 «2 \ d т)» Где m — масса частицы, dl — коэффициент орбитальной длины, и Вариационный принцип определения формы траектории 6 Дж / м 2 (E-U) dl = 0, (44,10) Где интеграл берется между двумя заданными пространственными точками.
Этот формат был введен Якоби. В свободном движении частицы U = 0, а (44.10) равно 3 Результаты флакона i J d l = 0, Другими словами, частицы движутся по прямой вдоль кратчайшего пути. Вернемся к формуле действия (44.3).
На этот раз параметр E также будет изменен. 6S = C-5E- (t-t0) SE-Ebt. IE Подставляя это в (44.2) m = t к ‘(4 4’ и) Для укороченного действия вида (44.9) это уравнение приводит к соотношению, которое является не чем иным, как интегралом уравнения (44.8). Наряду с траекторным уравнением движение полностью определяется.
Оспаривать Получить дифференциальное уравнение орбиты из вариационного принципа (44.10). Решения. Если вы сделаете вариацию, 6 [l / E-U dl = — [. LT-d l-V E -U ^ -d b r . J J 2 y / dE r-U dl) Во втором члене рассматривается dl dbl = dr dbr \ productioning, потому что dl2 = dr2.
В этом термине интеграл является частичным, а производная получается, если коэффициент 6r подынтегрального выражения равен нулю. Орбитальное уравнение 2 ^ T T 7 | (^ T T 7 |) = _ «. Разложив левую производную уравнения и введя силу F = —dU / dg, Это уравнение можно выразить как d2g _ F- (F t) t dl2 «2 (E-U)» Где t = dr / dl — единичный вектор касательной локуса.
разница F- (Ft) t является составляющей силы F n, перпендикулярной орбите. производная d2r / dl2 = dt / dl равно н / р Где R — радиус кривизны траектории, а n — единичный вектор главной нормали, перпендикулярной ей. Замена E-U на mv2 / 2 приводит к: По известным выражениям
Смотрите также:
| Скобки Пуассона в физике | Канонические преобразования в физике |
| Действие как функция координат в физике | Теорема Лиувилля в физике |
Если вам потребуется помощь по физике вы всегда можете написать мне в whatsapp.

