Оглавление:











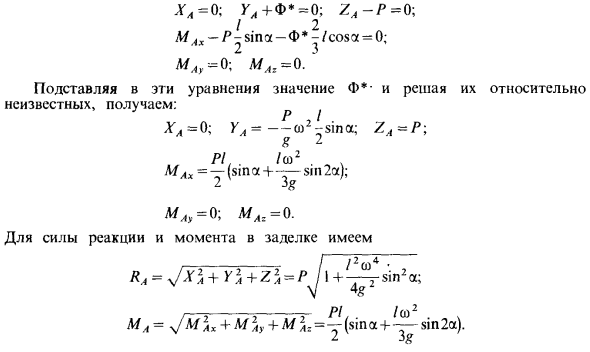

Принцип Даламбера
- Принцип Дарембеля материальных точек. Закон Ньютона включает в себя все необходимое для учета движения механической системы. Первоначально, однако, он использовался только для учета свободных материальных точек и свободных движений твердого тела. До тех пор пока аксиома отношений не будет сформулирована. Чтобы принять во внимание поведение проприетарных систем, Даламбер предложил специальный принцип, названный принципом Даламбера. Этот принцип был сформулирован в терминах «потерянного» движения.
В настоящее время уравнение движения несвободной материальной точки совпадает с уравнением движения свободного объекта, когда аксиома связывания считается справедливой. Только сила комбинированной реакции добавляется к активной или прикладываемой силе, действующей на точку. Современное представление принципа Даламбера не отличается от уравнений движения по содержанию, но более удобно для многих задач. Принцип Дарэмберта точки свободной материи эквивалентен основному закону динамики.
Можно ввести угловую скорость вращения вокруг мгновенного центра вращения, или, точнее, вокруг мгновенной оси, перпендикулярной плоскости движения, проходящей через мгновенный центр оси вращения. Людмила Фирмаль
Что касается негибких точек, то это эквивалентно основному закону с аксиомами отношений. Уравнение движения массы m массы точки для инерциальной системы отсчета под действием приложенной активной силы и реакции сцепления имеет вид ма = F + R (1) Сила F — результирующая сила активной силы, R — результирующая сила реакции привязки и ускорения точки относительно инерциальной системы отсчета. Инерционная сила материальной точки называется произведением вектора ускорения ^ с противоположным знаком к массе точки, то есть call = -that.
Когда использовать Рисунок g2 Точка и захват силы инерции передачи Получить все члены (1) в правой части уравнения G + H + F = 0. (2) Силы F, R и Ф (рис. 82) образуют систему сходящихся сил и соответствуют условию (2), поэтому это система сил, равная нулю. {G. Me, f} soo. (3) Уравнение (2) или эквивалентное условие (3) представляет принцип точек Даламбера: когда материальная точка движется, активная сила и объединенная реакция вместе с точечной инерцией образуют систему баланса сил.
Из проекции (2) на оси координат получите три условия для баланса сил. Ex + Yah + Фх = 0; Fy + Rf + Φ ,, = 0; Г2 + Я2 + Ф2 = 0. (4) Ускорение точки относительно инерциальной системы отсчета может быть разложено на компоненты вдоль оси декартовой системы координат. Кроме того, если движение точки считается состоящим из соотношения, рассматриваемого и относительного, его можно разбить на тангенциальное направление и нормальное ускорение, отношение рис, относительное и ускорение Кориолиса. Следовательно, сила инерции Ф может быть разложена на одни и те же компоненты. Ф = ФхГ + Ф / + Ф2Г = Ф2 + Фя = Фе + Ф, + Фх. (5) Касательная сила инерции F = Где ах — тангенциальное ускорение. Нормальная или центробежная инерция Здесь „- нормальное ускорение.
Переносимость и относительная сила инерции, а сила Кориолиса за счет ускорения выражается следующим образом. Φ, = -ta, Φ, = -ta, \ Φ, = -ta. Аналогично Фг выражаются через проекцию ускорения на декартову ось проекции силы инерции. Есть несколько аспектов инерционной силы. Согласно первому аспекту, уравнение движения (1) Чтобы дать более удобную форму равновесия (2), к точке условно применяется сила инерции, поэтому сила инерции Φ называется фиктивной, даренвальской, условной и т. Д.
С этой точки зрения Инерционная сила в принципе Даламбера — это не реальная сила, а нормальная сила, создаваемая движением тела, а также относительная сила инерции. Согласно другому наиболее распространенному аспекту, силы инерции считаются частично приложенными к «ускоряющим» объектам. Продемонстрировать следующие рассуждения. Масса движется с ускорением, но некоторые объекты действуют на нее с силой, равной (F + 1) (см. Рис. 83). Согласно закону о равенстве сил действия и реакции, масса должна иметь одинаковый модуль упругости для противодействия этим объектам, но направление противоположно — (F + H), который является силой инерции согласно (2).
Равен инерции, т. Е. Равен = — (T + H). Это соотношение дает основание полагать, что сила инерции применяется к объекту, который «ускоряется», то есть к объекту, который передает ускорение в точку. Фактически сила инерции Ф — векторная сумма действующих сил точек на «ускоряющем» теле. Это служит краткой оценкой этого действия. Однако, учитывая относительное перемещение точек, вводится соотношение. Кориолисова сила инерции f. Для движущегося наблюдателя их следует рассматривать как применимые к движущейся материальной точке, но невозможно показать материальное тело, действие которого в этой точке может объяснить эти силы. Портативная инерция и инерция Кориолиса являются частью общей инерции F.
Это также относится к общей инерции F, если невозможно показать объект, который генерирует его для части силы. Однако в этом случае ускорение тела. Этот объект представляет собой массу, которая движется с ускорением. Согласно третьей точке зрения, сила инерции считается приложенной к движущейся материальной точке. По крайней мере, это верно для наблюдателей, которые находятся в пределах системы отсчета для этой точки. Система отсчета для точки массы называется системой отсчета, где точка является стационарной, то есть ее относительная скорость и ускорение равны нулю.
В этой системе отсчета относительное равновесие сил Г + /? + Ф> 0, где Фр = -та’е — сила инерции переносимости в нашей собственной системе отсчета. Но в своей системе отсчета v’r = 0, a’r = 0, ускорение Кориолиса a ‘, = 0, a = a «e, поэтому Ф = Ф’е. Таким образом, принцип Даламбера является условием относительного баланса сил в его собственной системе отсчета. Для собственного наблюдателя, он применяется, потому что движущая сила инерции применяется к точке движения. Это согласуется с удельной силой инерции его собственной системы отсчета. Рис.
Инерционная сила F абсолютного движения. Сила в этом случае может рассматриваться как дополнительное действие на точку во вселенной. В терминах таких сил инерции необходимо изменить концепцию приложенных сил и изменить некоторые основные аксиомы динамики (см. Приложение). Принцип Даламбера материально-балльной системы Рассмотрим систему важных моментов. В общем, результаты активных сил и результаты реакций связывания применяются к каждой точке системы. Применяя принцип Даламбера к каждой точке системы: Pk + Dk + Fk = 0, k = 1, 2, N, (6) Где Фк = ––––– — сила инерции k-й точки (рис. 83). Условие (6) может быть выражено в эквивалентном формате. Rk, Ф *} оо, * = 1,2, …, N; (7) N-векторное условие (6) или (7) представляет принцип Даламбера системы.
- По мере движения механической системы активные силы, объединенные реакции и силы инерции образуют систему баланса сил в каждой точке системы. Принцип Даламбера системы по своему содержанию ничем не отличается от уравнения движения точки системы. Представьте себе, что результирующая сила, приложенная к каждой точке в системе, подразделяется на внутренние и внешние силы по всей системе, а не на активные силы и реакцию сцепления. Fk + Rk = Fj? + Fp. Принцип системы Даламбера затем может быть выражен в другой форме. ^ ‘+ Оо + Φ11 = 0, k = 1, 2, …, LG. (8) Из принципа Даламбера системы вида (6) или (8) Рисунок 83 Получить 6 результатов в Условия равновесия сил, действующих на системные точки, и сил инерции.
Суммируя левую часть (6) во всех точках системы, E E D> + ZФ * = о. (9) Умножим каждое соотношение (6) слева на радиус-вектор точки rk и снова суммируем точки системы: к. ft xA) + ((rxЛ,) + ((f, xφ) = 0 или 1 M0 (Fk) + M M0 (Rk) + Л? 0 (Φk) = 0 (10) Следствие принципа Даламбера (10) справедливо как для стационарных, так и для движущихся точек в инерциальной системе отсчета системы, поскольку начало вектора радиуса gk можно выбрать в любой точке. Условия (9) и (10) дают шесть условий равновесия, которые аналогичны условиям равновесия сил, приложенных к телу в статике, когда они представлены проекцией на оси координат. Используя принцип Даламбера в форме (8), результат получается в следующем виде: ED ´ + EF ^ O; (11) Мо Мо (F?) + Яо (Φ *) — 0, (12).
Далее, при тех же условиях, когда несколько цепных линий разной длины помещаются на две прямые в равновесии, все они оказываются одинаковыми для точки р. Людмила Фирмаль
Поскольку внутренняя сила системы благодаря этим силовым характеристикам удовлетворяет условиям Diao; я? o (A °) = o. Если (11) и (12) спроецировать на оси координат, шесть равновесных силовых состояний могут быть получены снова. Характерной чертой баланса сил в виде (11) и (12) является отсутствие в них внутренних сил, что особенно полезно для решения многих задач системной динамики. Фактически условие (11) является изменением теоремы об импульсе, а (12) является следующей теоремой. Изменение системного момента движения (если представлено в форме) Dp » -‘in-O; II G | Дм «м-» = о. В).
Сравнение (11) с (1G) и (12) с (12 ‘) дает уравнения, которые вычисляют главный вектор системы и момент инерции относительно импульса и импульса. «• — (13) (, 4> В точке (12 ‘) точка О неподвижна в выбранной инерциальной системе отсчета. Поэтому, используя уравнение (14), главный момент инерции можно рассчитать только для неподвижной точки O. Для движущейся точки вместо (12 ‘) нам нужно использовать ранее доказанную теорему для изменения момента движения движущейся точки A-. T, I, + «D». (12 ‘) После замены точки O в A в (12) и сравнения с (12 «) получите формулу для расчета основного момента инерции для точки перемещения A. £ (Φ> = — ^ L + Mvcxva = ~ + vAx Mvc ^. (14 ‘).
В уравнении (14 ‘) vA и vc являются скоростями точки A и центра тяжести C соответственно относительно рассматриваемой инерциальной системы координат. М — масса системы. Q — Mvc, поэтому основным вектором инерции является Ф = £ Фк = — ^ = -Л / ас. (15) Где M — масса системы, а vc и ac — скорость и ускорение в центре масс, соответственно. Для этих твердых движений, если сила инерции уменьшается до результата, последний будет иметь абсолютное значение и направление, которое соответствует главному вектору этих сил. Однако результат инерции не обязательно проходит через центр тяжести тела, но его модуль и направление всегда определяются уравнением (15).
Когда вектор из (14) проецируется на ось Oz, он становится следующим. < «■> Аналогичные выражения могут быть получены для других осей. Как известно, в случае вращения твердого тела вокруг неподвижной оси Oz, Ks = Jzw. Подставляя это значение K в (14 «) или MF) = Л / г (Φk) = -Ле. (16) Уравнение (16) вычисляет момент инерции относительно оси вращения при вращательном движении твердого тела вокруг неподвижной оси. Этот момент создается тангенциальной силой инерции. Это потому, что моменты не создаются, потому что нормальная сила инерции в каждой точке тела пересекает ось вращения. Другой результат исходит из принципа системы Дарлемберта — теоремы об изменении кинетической энергии.
Чтобы сделать это, умножьте скаляр в (8) на drk и суммируйте полученное соотношение во всех отношениях. получить Е ^ le> ‘d4 + ЕЕ $ * • > = Л? СC (PD) = 0. Фактически, согласно следствиям принципа Даламбера центра тяжести (12) Х л? S (Pe ’) + £? ‘= O Во время перевода тело не вращается вокруг центра тяжести, поэтому X ^ c (A * ‘,) = 0. Следовательно, ££ «= 0. При вращении вокруг неподвижной оси. Если вы выберете точку O центра вращения Oz в качестве центра инерции, то в этой точке будут получены главный вектор и главный момент инерции. Φ = -Wc; D ^ = -dRo / dt. Если центр тяжести находится на оси вращения, Φ = 0.
Проекция главного момента инерции на неподвижные оси в общем случае может быть рассчитана по формуле L ™ = -dKx / dt * O. L ™ = -dA ^ / d / ^ O; L? > = -dKJdt = -J & Моменты инерции £ <® * и L1® ‘рассчитываются в следующем разделе. Если оси Oz являются главными осями инерции точки O, они равны нулю. В плоском движении. Если вы выберете центр тяжести в качестве центра уменьшения инерции, вы получите главный вектор и главный момент инерции в этой точке. Для основного вектора силы инерции, F = — форель. Для главного момента инерции относительно центра масс C, который является точкой перемещения плоского движения объекта, получим ту же формулу, что и формулу (14), полученную для неподвижной точки O.
Согласно результату принципа Даламбера (12) главный момент инерции относительно центра тяжести удовлетворяет следующему условию £ jWc (Fle>) + Zb® ‘= 0. С другой стороны, из теоремы относительно изменения момента движения относительно центра тяжести абсолютного и относительного dKc / dt = £ A7C (TG); dK? / DT = ^ MS (GG). Из этих отношений £ 0. Подставляя приобретенную стоимость в (а) Давление призмы за счетчиком будет F «= -F ‘, давление призмы Чтобы определить натяжение нити $, значение ускорения можно рассчитать по формуле (б) или (б) Пример 2. Однородный тонкий стержень АВ Я прочно закреплен на вертикальной оси ГС под углом а (рис. 85, а). Вал 00 вращается со стержнем AB с постоянной угловой скоростью ω.
Определить реакцию стержня на конце А. Решения. Примените результат принципа Даламбера в виде силы равновесия к внешним и инерционным силам стержня AB. Векторные моменты неизвестной реакции RA и конца M1 вытянуты вдоль координатных осей. Если вы разделите весь стержень на основные секции одинаковой длины, ускорение в каждой точке стержня равно a = r4sh2, поэтому ускорение в средней точке этих участков линейно распределяется вдоль стержня ( Расстояние от точки до оси) вращение. Силу инерции основного сечения стержня также принимают за точку, распределенную по линейным законам, образующую треугольник. Распределенные таким образом параллельные силы имеют результирующую силу, и их линия действия отстоит от основания треугольника на расстоянии 2/3 / от вершины треугольника на расстоянии / jJ вдоль стержня. вы.
Результирующая сила Ф * всегда равна главному вектору силы, всегда распределенному вдоль треугольника. Для основного вектора силы инерции, F = -масса Штанга, т переменное ускорение Промежуточная точка. Вот так. Состоит из шести состояний стержня рассматриваемого момента, расположенного в координатной плоскости Айз. Далее проекция силы и ее момента на оси координат Ax, Ay, Az выглядит следующим образом. Рисунок 85 LG4 = O; X ^ + Φ * = 0; ZA-P = O-, M Ax-P-sina-Ф * — / cosa = 0; мА, = o-. MA = 0. Подстановка значений Ф * в эти уравнения и решение для неизвестных дает: ML> = 0; MLg = 0. Для силы реакции и момента уплотнения, ML = Jm 1Lx + M1Ly + M2Lr = ^ — (mt <1 + sin 2a).
Смотрите также:
Задачи по теоретической механике
| Силовая функция и потенциальная энергия системы | Принцип Даламбера для материальной точки |
| Закон сохранения механической энергии | Принцип Даламбера для системы материальных точек |

