Оглавление:
Системы, содержащие логарифмы с переменными основаниями
Примеры с решениями
Пример №219.
Решить систему уравнений
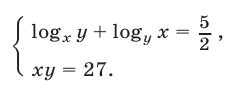
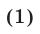
Решение:
Используя формулу 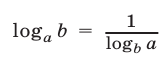 и полагая
и полагая 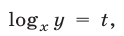 запишем первое уравнение системы (1) в виде
запишем первое уравнение системы (1) в виде 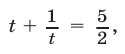 откуда
откуда 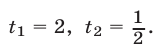
Если 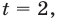 то
то 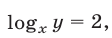 откуда
откуда
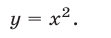
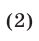
Из (2) и второго уравнения системы (1) находим 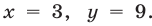 Аналогично, если
Аналогично, если 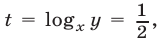 то
то 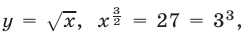 откуда
откуда 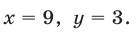
Ответ. 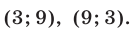
Пример №220.
Решить систему уравнений
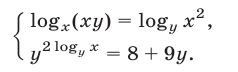
Решение:
Допустимые значения 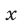 и
и 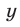 определяются условиями
определяются условиями

При выполнении условий (5) систему (3), (4) можно записать в виде
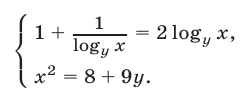
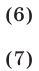
С помощью замены 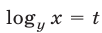 уравнение (6) приводится к квадратному уравнению
уравнение (6) приводится к квадратному уравнению 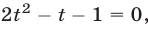 имеющему корни
имеющему корни 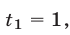

1) Если 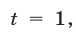 то
то 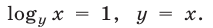 Подставляя
Подставляя 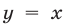 в (7), получаем уравнение
в (7), получаем уравнение 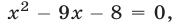 имеющее единственный положительный корень
имеющее единственный положительный корень 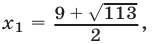 которому соответствует
которому соответствует 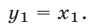
2) Если 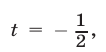 то
то 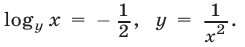 Подставляя
Подставляя 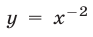 в (7), получаем биквадратное уравнение
в (7), получаем биквадратное уравнение 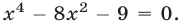 Полагая
Полагая 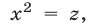 приходим к уравнению
приходим к уравнению 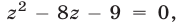 откуда
откуда 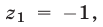
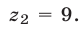 Так как уравнение
Так как уравнение 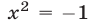 не имеет действительных корней, а уравнение
не имеет действительных корней, а уравнение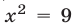 имеет единственный положительный корень
имеет единственный положительный корень 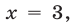 то пара чисел
то пара чисел 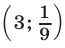 образует решение системы (3), (4).
образует решение системы (3), (4).
Ответ. 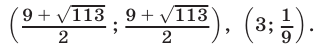
Пример №221.
Решить систему уравнений
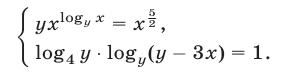
Решение:
Логарифмируя уравнение (8) по основанию 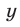 , получаем
, получаем
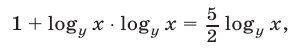
откуда следует, что 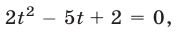 где
где 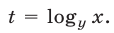 Это квадратное уравнение имеет корни
Это квадратное уравнение имеет корни 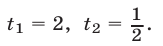
1) Если 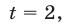 то
то 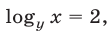 и значит,
и значит,
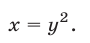
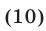
Используя формулу 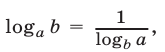 запишем уравнение (9) в виде
запишем уравнение (9) в виде 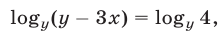 откуда
откуда
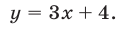
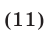
Из системы (10), (11) получаем уравнение 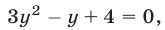 не имеющее действительных корней.
не имеющее действительных корней.
2) Если 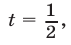 то
то 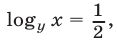 откуда
откуда 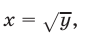
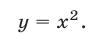
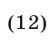
Из системы (11), (12) следует, что 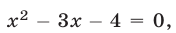 , откуда
, откуда 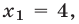
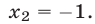 Так как
Так как 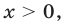 то значение
то значение 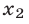 следует отбросить, а значению
следует отбросить, а значению 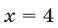 соответствует
соответствует 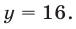
Ответ. 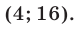
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

