Оглавление:
Рациональные неравенства. Метод интервалов
Примеры с решениями
Пример №255.
Решить неравенство
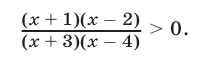
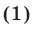
Решение:
Заметим, что линейная функция  меняет знак при переходе через точку
меняет знак при переходе через точку причем правее точки
причем правее точки  эта функция положительна, а левее точки
эта функция положительна, а левее точки  — отрицательна.
— отрицательна.
Отметив на числовой оси точки  , которые являются нулями (корнями) многочленов, стоящих в числителе и знаменателе дроби (1), разобьем числовую ось на пять промежутков (рис. 21.1).
, которые являются нулями (корнями) многочленов, стоящих в числителе и знаменателе дроби (1), разобьем числовую ось на пять промежутков (рис. 21.1).
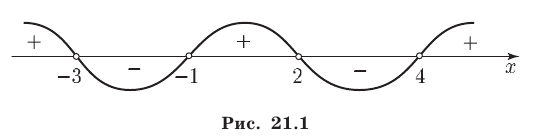
На самом правом промежутке 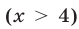 дробь (1) положительна, так как все множители в числителе и знаменателе этой дроби положительны при
дробь (1) положительна, так как все множители в числителе и знаменателе этой дроби положительны при  .
.
При переходе через каждую из отмеченных точек один и только один из этих множителей меняет знак, и поэтому знак дроби каждый раз меняется. Учитывая это, расставим знаки дроби (рис. 21.1). Итак, множество решений — объединение интервалов 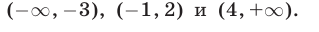
Ответ. 
Рассмотренный способ решения неравенств называется методом интервалов. Он применяется обычно при решении рациональных неравенств, т. е. неравенств вида


где 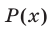 и
и  — многочлены.
— многочлены.
Пример №200.
Решить неравенство
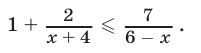

Решение:
Преобразуем неравенство (3) к стандартному виду (2):
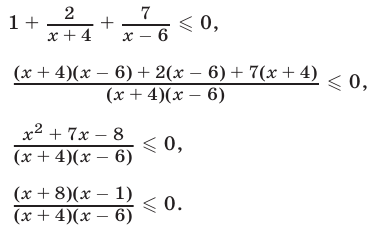
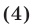
Неравенство (4) равносильно неравенству (3). Отметив на числовой оси точки 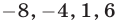 (рис. 21.2), определим знаки рациональной функции, стоящей в левой части неравенства (4).
(рис. 21.2), определим знаки рациональной функции, стоящей в левой части неравенства (4).
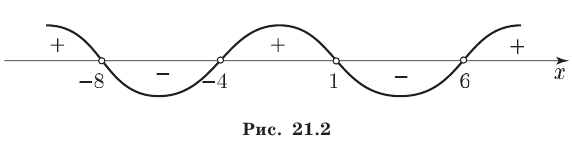
Заметим, что числа  и
и  являются решениями неравенства (4), а числа
являются решениями неравенства (4), а числа 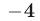 и
и  не принадлежат множеству решений.
не принадлежат множеству решений.
Ответ. 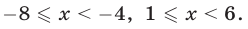
Пример №256.
Решить неравенство
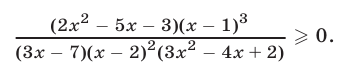
Решение:
Квадратный трехчлен  имеет корни
имеет корни 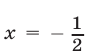 и
и 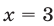 . Поэтому
. Поэтому  Квадратный трехчлен
Квадратный трехчлен  принимает положительные значения при всех
принимает положительные значения при всех 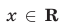 , так как его дискриминант
, так как его дискриминант 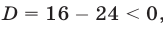 а старший коэффициент положителен.
а старший коэффициент положителен.
Обозначим левую часть неравенства через 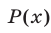 . Функция
. Функция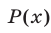 не определена при
не определена при 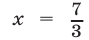 и
и 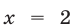 и меняет знак при переходе через точки
и меняет знак при переходе через точки 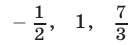 и
и 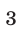
Числа 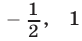 и
и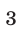 (корни уравнения
(корни уравнения 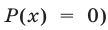 являются решениями данного неравенства. Строгое неравенство
являются решениями данного неравенства. Строгое неравенство  при
при  равносильно неравенству
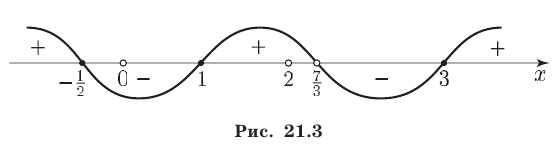
равносильно неравенству 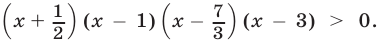 Применяя метод интервалов (рис. 21.3), находим все решения исходного неравенства с учетом того, что числа
Применяя метод интервалов (рис. 21.3), находим все решения исходного неравенства с учетом того, что числа  и
и 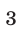 принадлежат множеству решений неравенства, а число
принадлежат множеству решений неравенства, а число 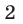 не принадлежит этому множеству.
не принадлежит этому множеству.
Ответ. 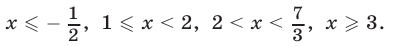
Пример №257.
Решить неравенство
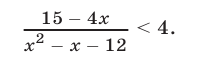
Решение:
Данное неравенство равносильно каждому из следующих неравенств:
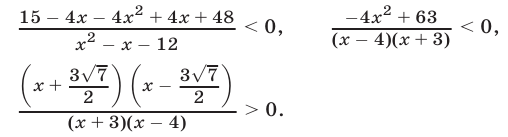
Заметив, что 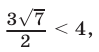 а
а 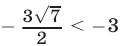 (поскольку
(поскольку  ), и применив метод интервалов (рис. 21.4), найдем решения исходного неравенства.
), и применив метод интервалов (рис. 21.4), найдем решения исходного неравенства.
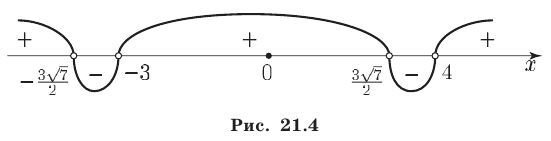
Ответ. 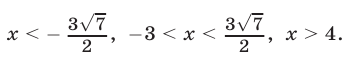
Пример №258.
Решить неравенство
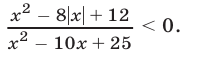
Решение:
Рассмотрим два случая: 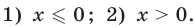
1)Если 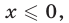 то
то 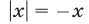 и неравенство примет вид
и неравенство примет вид
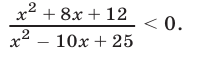
Это неравенство равносильно следующему:
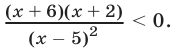
Отсюда находим 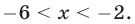
2) Если  , то исходное неравенство (при условии
, то исходное неравенство (при условии 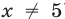 ) равносильно неравенству
) равносильно неравенству 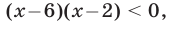 откуда получаем
откуда получаем 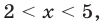
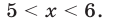
Ответ. 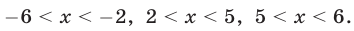
Пример №259.
Решить неравенство
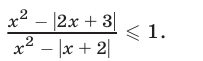
Решение:
Разобьем числовую прямую на три промежутка точками 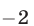 и
и 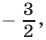 при переходе через которые меняют знак линейные функции
при переходе через которые меняют знак линейные функции  и
и 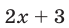 соответственно.
соответственно.
1) Если  то исходное неравенство равносильно каждому из
то исходное неравенство равносильно каждому из
неравенств
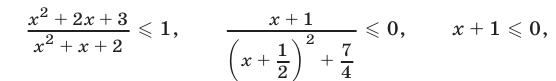
откуда, учитывая условие 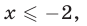 получаем
получаем 
2) Если  , то исходное неравенство равносильно каждому из неравенств
, то исходное неравенство равносильно каждому из неравенств
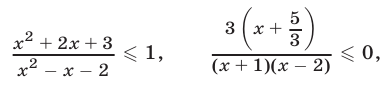
откуда 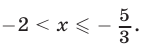
3) Если 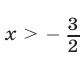 , то исходное неравенство равносильно каждому из неравенств
, то исходное неравенство равносильно каждому из неравенств
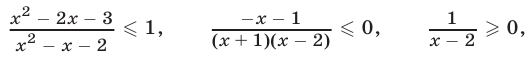
откуда 
Ответ. 
Пример №260.
Решить неравенство
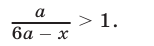

Решение:
Неравенство (5) равносильно каждому из следующих неравенств:
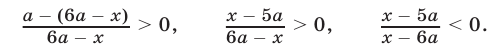
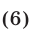
При 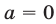 неравенство (6) не имеет решений.
неравенство (6) не имеет решений.
Пусть 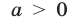 , тогда
, тогда  и множество решений неравенства (6) — интервал
и множество решений неравенства (6) — интервал 
Пусть  тогда
тогда 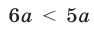 и множество решений неравенства (6) — интервал
и множество решений неравенства (6) — интервал 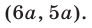
Ответ. Если  , то
, то  если
если  , то решений нет; если
, то решений нет; если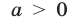 , то
, то 
Пример №261.
Найти все значения 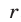 , при которых вершины двух парабол
, при которых вершины двух парабол
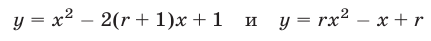
лежат по разные стороны от прямой 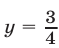
Решение:
Вершины парабол лежат по разные стороны от прямой 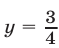 тогда и только тогда, когда числа
тогда и только тогда, когда числа 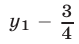 и
и 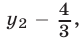 где
где 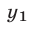 и
и 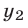 — ординаты вершин парабол, имеют разные знаки, т. е.
— ординаты вершин парабол, имеют разные знаки, т. е.
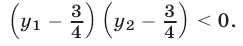
Чтобы найти  и
и 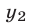 , воспользуемся методом выделения полного квадрата. Получим
, воспользуемся методом выделения полного квадрата. Получим
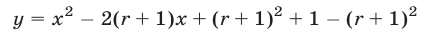
Отсюда следует, что
и
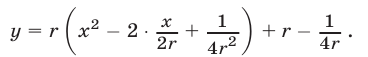
Подставляя выражения для  и
и 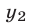 в левую часть неравенства (7), получаем неравенство
в левую часть неравенства (7), получаем неравенство
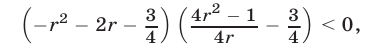
равносильное следующему:

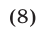
Разложив левую часть неравенства (8) на множители, получим равносильное ему неравенство
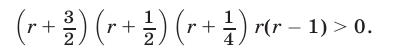
С помощью метода интервалов (рис. 21.5) найдем искомые значения 
Ответ. 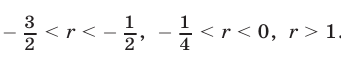
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

