Оглавление:
Системы тригонометрических уравнений
Рассмотрим некоторые типы систем тригонометрических уравнений и укажем наиболее употребительные методы решения систем, основываясь на общей теории систем уравнений, изложенной в §15.
Примеры с решениями
Пример №222.
Решить систему уравнений
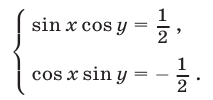
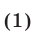
Решение:
Складывая и вычитая уравнения системы (1), получаем систему
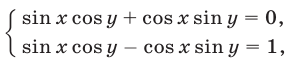
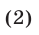
равносильную (1). Систему (2) можно записать в виде
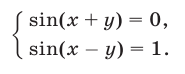
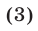
Из системы (3) находим
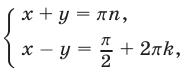
где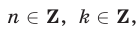 
откуда следует, что
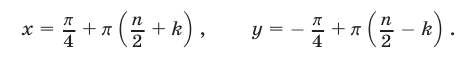
Ответ.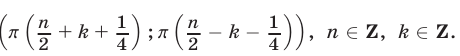 
Замечание. Обратим внимание на типичную ошибку, которую допускают учащиеся и абитуриенты при записи решений систем тригонометрических уравнений. Дело в том, что параметры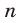 
и 
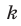появляются при решении разных уравнений системы (3) и независимы друг от друга. Поэтому эти параметры должны обозначаться разными буквами. Обозначение их одним символом ведет к потере решений.
В некоторых случаях системы тригонометрических уравнений можно свести к алгебраическим системам.
Пример №223.
Решить систему уравнений
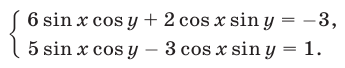
Решение:
Полагая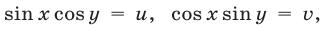 
получаем систему уравнений
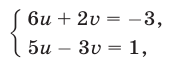
откуда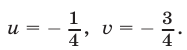 
Исходная система равносильна каждой из следующих систем:
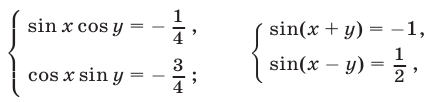
откуда следует, что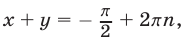 
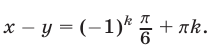
Ответ.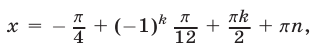 
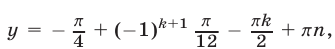
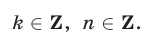
Пример №224.
Решить систему уравнений
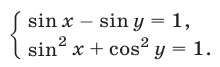
Решение:
Полагая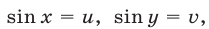 
получаем алгебраическую систему
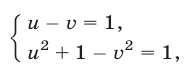
равносильную системе
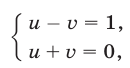
откуда находим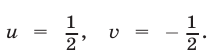 
Таким образом,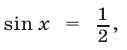 
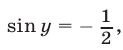откуда
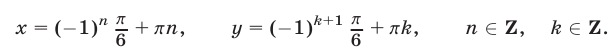
Ответ.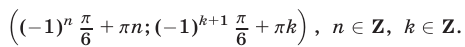
Аналогично можно находить решения систем вида
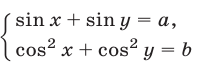
и
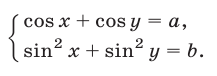
Решая системы тригонометрических уравнений с двумя неизвестными, следует выяснить, нельзя ли выразить одно неизвестное через другое и свести задачу к решению уравнения с одним неизвестным.
Пример №225.
Решить систему уравнений
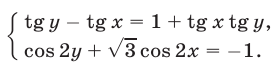
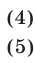
Решение:
Система (4), (5) имеет смысл, если
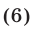
Преобразуем сначала уравнение (4), разделив обе его части на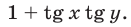 
Тогда это уравнение примет вид
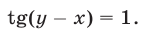
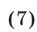
Однако следует иметь в виду, что эта операция может привести к потере решений исходной системы, а именно таких решений, для которых
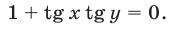
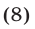
Если справедливо равенство (8), то из (7) находим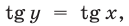 
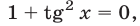что невозможно.
Итак,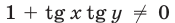 
и поэтому система (4), (5) равносильна системе (7), (5) при выполнении условий (6).
Из уравнения (7) находим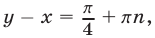 
откуда
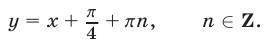
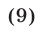
Подставляя найденное для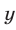 
выражение в уравнение (5), получаем
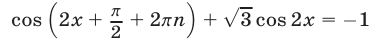
или
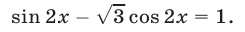
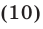
Применяя метод введения вспомогательного угла, запишем уравнение (10) в виде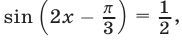 
откуда
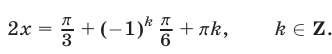
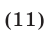
Если 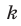— четное число 
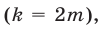то из равенства (11) получаем 
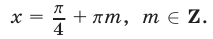Подставив это выражение для 
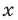в формулу (9), найдем 
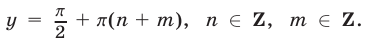Но тогда
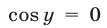и не выполняются условия (6).
Если же 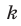— нечетное число 
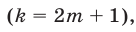то из (11) следует, что 
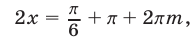откуда
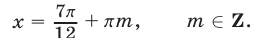
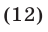
Из (12) и (9) находим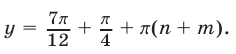 
Полагая 
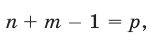имеем
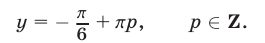
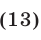
Для значений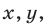 
определяемых формулами (12) и (13), выполняются условия (6) и поэтому соответствующие пары чисел образуют решения системы (4), (5).
Ответ.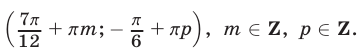 
Пример №226.
Решить систему уравнений
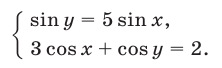
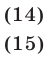
Решение:
Будем решать данную систему методом исключения одного из неизвестных, например у. Для этого запишем уравнение (15) в виде
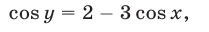
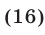
а затем возведем в квадрат обе части уравнений (14) и (16) и результаты сложим. Получим
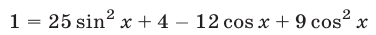
или
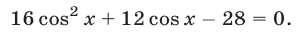
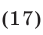
Заметим, что система (15), (17) является следствием системы (14), (15), а уравнение (17), равносильное уравнению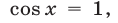 
имеет корни
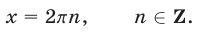
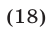
Подставляя найденные значения 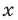в уравнение (15), получаем 
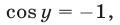откуда
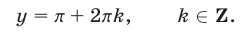
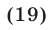
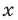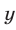Значения и , определяемые формулами (18) и (19), образуют решения не только системы (15), (17), но и исходной системы.
Ответ.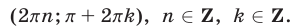
Рассмотрим еще несколько систем тригонометрических уравнений, при решении которых можно применять метод исключения одного из неизвестных.
Пример №227.
Решить систему уравнений
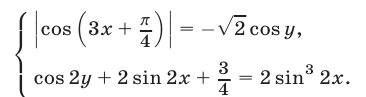
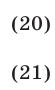
Решение:
Чтобы исключить из системы (20), (21) неизвестное , возведем обе части уравнения (20) в квадрат:
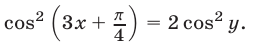
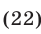
Так как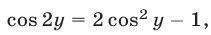 
, то из (22) и (21) следует, что
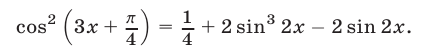
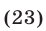
Уравнение (23) можно записать в виде
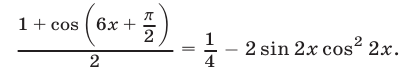
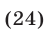
Применяя формулы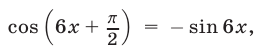 
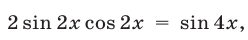
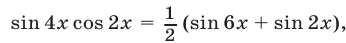заменим уравнение (24) ему равносильным :
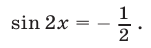
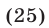
Уравнение (25) является следствием системы (20), (21) и поэтому указанная система равносильна системе, состоящей из уравнений (20), (25) и уравнения, полученного из (21) в результате замены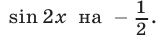 
Такое уравнение имеет вид
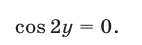
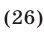
Из (20) следует, что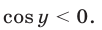 
Поэтому 
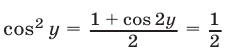в силу (26) и 
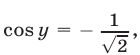откуда 
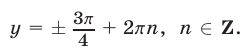Соответствующие значения 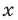найдем, решив уравнение (25).
Ответ.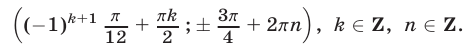 
Пример №228.
Решить систему уравнений
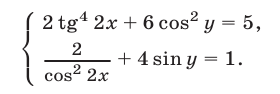
Решение:
Используя формулу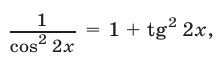 
запишем уравнение (28) в виде
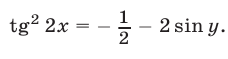
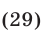
После исключения неизвестного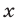 
из системы (27), (29) получаем 
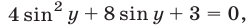откуда 
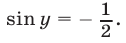Следовательно, 
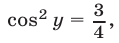а затем из уравнения находим 
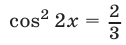или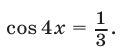 
Ответ.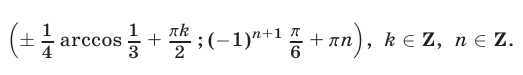
Пример №229.
Решить систему уравнений
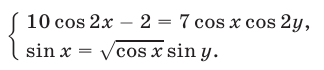
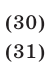
Решение:
Возведя обе части уравнения (31) в квадрат, получаем
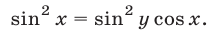
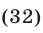
Система (30), (32) является следствием системы (30), (31). Используя формулу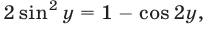 
запишем уравнение (32) в виде
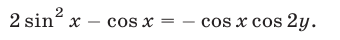
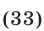
Сложим почленно уравнение (30) с уравнением (33), умноженным на 7:
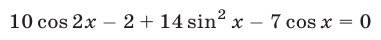
или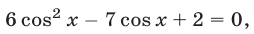 
откуда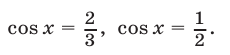 
1) Если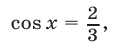 
то либо
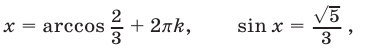
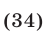
либо
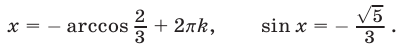
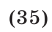
Из (34) и (31) следует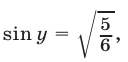 
откуда 
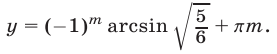Аналогично, из (35) и (31) находим 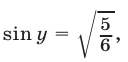откуда получаем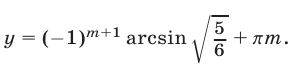 
2) Если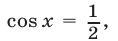 
то из (31) следует, что 
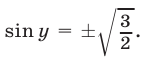В этом случае система (30), (31) не имеет решений.
Ответ.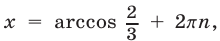 
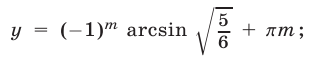
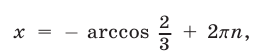
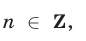
Пример №230.
Найти все решения системы уравнений
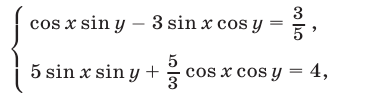
удовлетворяющие условиям
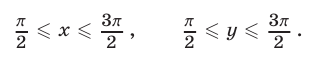
Решение:
Умножим уравнение (37) на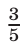 
, затем обе части полученного уравнения возведем в квадрат и сложим почленно с уравнением, образующимся при возведении в квадрат обеих частей уравнения (36). В результате придем к уравнению
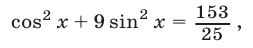
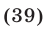
являющемуся следствием системы (36), (37). Уравнение (39) равносильно уравнению
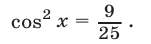
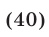
Решив уравнение (40) при условиях (38), находим два его корня
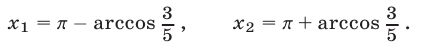
Если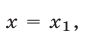 
то 
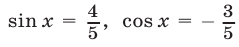и система (36), (37) примет вид
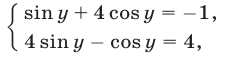
откуда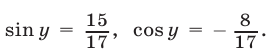 
Учитывая условия (38), получаем 8
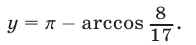
Если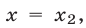 
то 
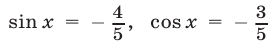и система (36), (37) примет вид
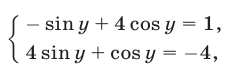
откуда находим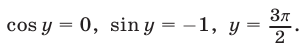 
Ответ.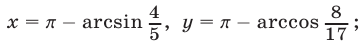 
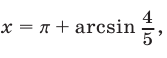
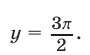
Пример №231.
Решить систему уравнений
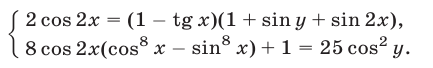
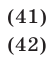
Решение:
Система имеет смысл, если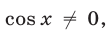 
а уравнение (41) равносильно уравнению
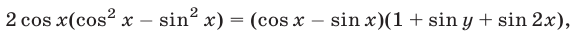
откуда следует
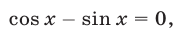
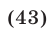
либо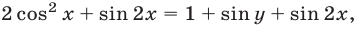 
т. е.
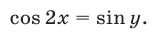
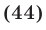
Преобразуем далее уравнение (42), пользуясь тем, что
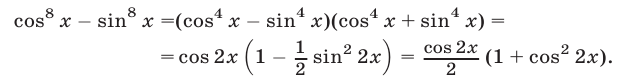
Тогда уравнение (42) можно записать в виде
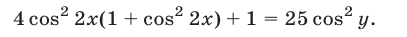
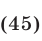
Исходная система (при условии, что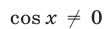 
) равносильна совокупности систем (43), (42) и (44), (45).
1) Рассмотрим систему (43), (42). Уравнение (43) равносильно уравнению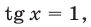 
откуда находим
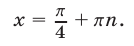
Из (42) и (43) следует, что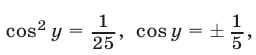 
откуда
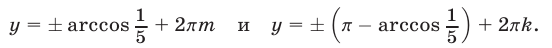
Эти два множества значений 
можно описать одной формулой:
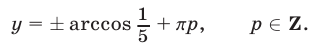
Укажем еще один способ записи корней уравнения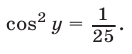 
Так как 
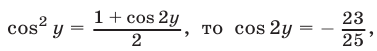откуда
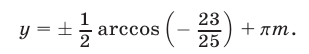
2) Обратимся теперь к системе (44), (45). Исключая из этой системы 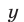, получаем уравнение
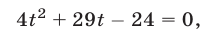
где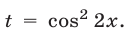 
Отсюда 
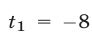(этот корень следует отбросить),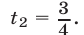 
Итак,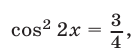 
откуда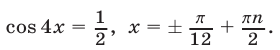 
Из (44) находим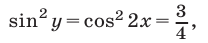 
откуда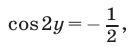 
Ответ.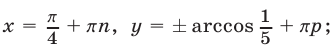 
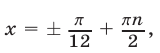
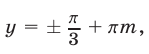
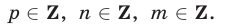
Пример №232.
Решить систему уравнений
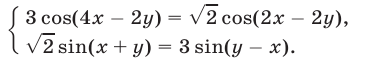
Решение:
Перемножив почленно уравнения (46) и (47), получим
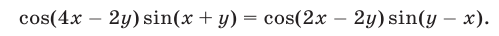
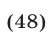
Уравнение (48), являющееся следствием системы (46), (47), равносильно каждому из следующих уравнений:
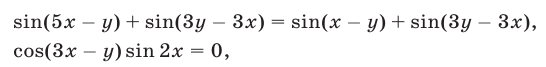
откуда находим, что либо
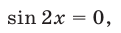
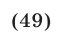
либо
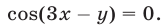
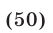
Система (46), (47) равносильна совокупности двух систем (46), (47), (49) и (46), (47), (50).
1) Рассмотрим систему (46), (47), (49). Из (49) следует, что
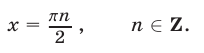
Подставляя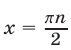 
в систему (46), (47), получаем
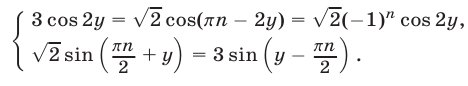
Из (51) следует, что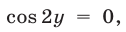 
откуда 
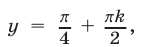где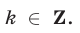 
Подставляя найденное значение 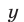в уравнение (52), находим
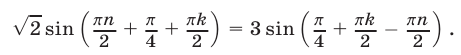
Равенство (53) не может быть верным ни при каких целых 
и 
, так как
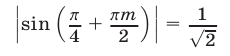при любом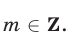 
Следовательно, система (46), (47), (49) не имеет решений.
2) Рассмотрим систему (46), (47), (50). Из (50) следует, что
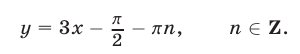
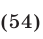
Подставляя это значение 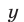в систему (46), (47), находим
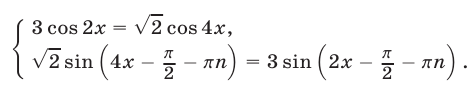
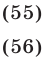
Уравнение (56) равносильно уравнению (55), так как
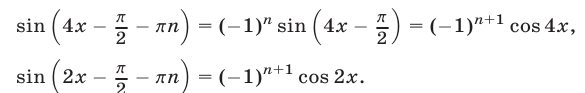
Используя формулу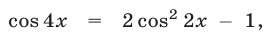 
из (55) находим 
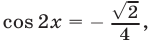откуда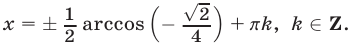 
Соответствующие значения 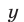определяются формулой (54).
Ответ.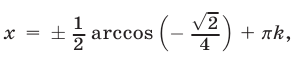
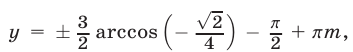
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
