Примеры построения ядра сечения
Построим ядро сечения прямоугольной формы (рис.123). Площадь и моменты инерции сечения
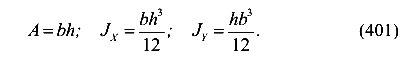
Квадраты радиусов инерции сечения
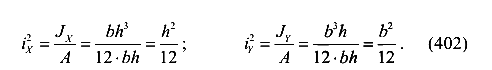
Отсеченные отрезки первой нулевой линии (рис.129)
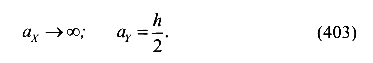
Координаты соответствующей точки приложения силы
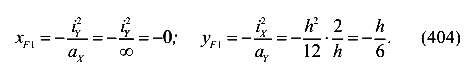
Отсеченные отрезки второй нулевой линии
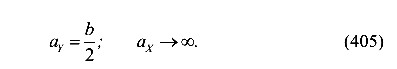
Координаты соответствующей точки приложения силы
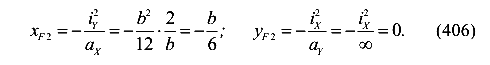
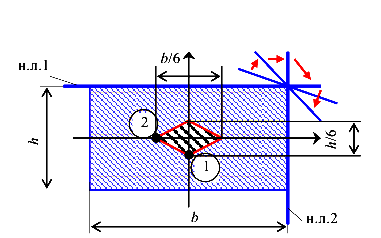
Откладываем точки 1 и 2 на сечении. Из положения 1 в положение 2 нулевая линия, оставаясь касательной к сечению, попадает путем поворота около точки S. Каждому положению нулевой линии соответствует какая-то точка приложения силы. Так как нулевая линия поворачивается около неподвижной точки S, то точка приложения силы движется по прямой линии. Так как нулевая линия при этом в процессе поворота остается
касательной к сечению, то отрезок 1-2 является частью контура ядра сечения.
Очевидно, что ядро прямоугольного сечения имеет форму ромба, каждая полудиагональ которого равна одной третьей полуразмера сечения (рис. 123).
Построим ядро для сечения круглой формы (рис. 124).
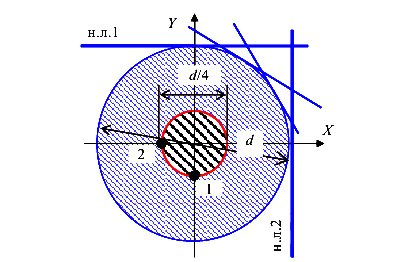
Площадь и моменты инерции сечения
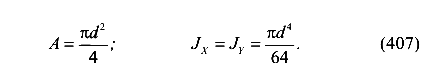
Квадраты радиусов инерции сечения
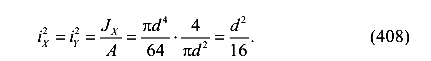
Отсеченные отрезки нулевой линии 1
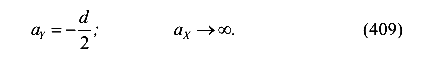
Координаты точки приложения силы, соответствующие нулевой линии 1.
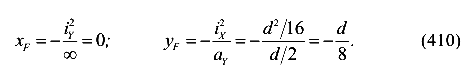
Отсеченные отрезки нулевой линии 2
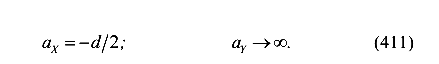
Координаты точки приложения силы
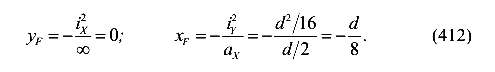
Очевидно, что нулевая линия не может попасть из положения 1 в положение 2, оставаясь касательной к сечению и поворачиваясь около неподвижной точки. Нулевая линия из положения 1 в положение 2 может попасть, оставаясь касательной к сечению только поворачиваясь около подвижной точки, движущейся по контуру круглого сечения. Поэтому контур ядра сечения является кривой — окружностью (рис. 124).
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны:
| Ядро сечения |
| Свойства ядра сечения |
| Порядок расчета внецентренно сжатой колонны |
| Изгиб с растяжением или сжатием |

