Оглавление:
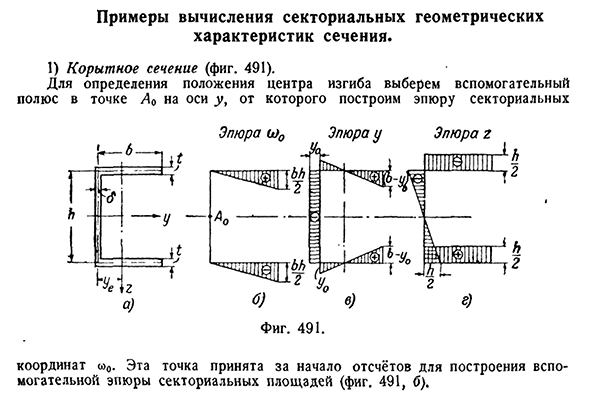






Примеры вычисления секториальных геометрических характеристик сечения
- Приведен пример расчета геометрических характеристик участка сечения. 1) поперечное сечение сваи (рис. 491). Чтобы определить положение центра сгиба, выберите вспомогательный полюс в точке Lo на оси Y. Н2 Четыре. Координата w0 эта точка считается началом отсчета для построения вспомогательных участков участка
сектора (рис. 491, б).§ 1 8 1] Пример расчета характеристик сектора 5 6 5 Для использования формулы (30.40) необходимо рассчитать секторные линейные статические моменты S и s^»»OJ’DF и S a^=§ (£) Oz dF. Эти интегралы могут быть вычислены методом
Верещагина (см.§ 131) путем умножения площади участка на ординату участка Людмила Фирмаль
y или z под центроидом областиb t — ^имея это в виду, мы, наконец, получаем: ТАК п-ИОТ+ч б я'(30.42) az=0, так как S » >0>= (Из-за того, что кривая<£0 антисимметрична, а график u-симметричен). Знак минус АС указывает на то, что полученное значение АС следует отложить от точки влево. Теперь, используя формулу (30.41), перейдем к нахождению главной нулевой точки сектора на контуре разреза. Как уже упоминалось, для поперечного сечения с осью симметрии нулевая точка находится на пересечении этой оси
со средней линией поперечного сечения. Чтобы узнать, как найти главное нулевое равноденствие, рассмотрим его положение как неизвестное и воспользуемся общим решением формулы (30.41) для его нахождения. Для этого из главного полюса A (местоположение которого уже найдено) возьмем любую точку 1 в качестве начала отсчета и построим график координат сектора, >»3<О’= = аых;>>4^У ч-~= — ~(б-2а г}. Владеет моментом инерции полки немного
- пренебрегая.5 6 6 основы расчета тонкостенных стержней[гл. XXX Соответствующий участок разделенных координат состоит из фигур. 492, б. Секторно-реальный статический момент u’BDS теперь можно вычислить как сумму произведения площади участка на соответствующую полку (/) и толщину стенки 0X): с»=С * частей 4bt+4aumi+я(2ч) (2л+П1)=■Ф- Затем по формуле (30.41) определяют секторные координаты нулевой точки от выбранной опорной точки: И Как видно из построенного графика)= ZT — это Jhay, (b—a^h h~12+6 ’b; Если вы присвоите вышеуказанное значение (30.42) ay, вы получите: _b * hH2L&x+3^12 ’Gbt+h’ (30.43) I1 8 1] Пример расчета характеристик
сектора 5 6 7 Наконец, легко вычислить значение статического момента сечения для отсеченной части сечения, используя график основных координат разделения Этот Интеграл равен площади срезаемой части участка®. Шах-б * Два. (30.45)) 4568 база[гл. XXX Для стен SL0 равен нулю, поскольку график антисимметричен и sum|*codF=0. Таким образом, нет касательной сектора к стене Ф (3) Т-образное сечение. Так как главный разделительный полюс находится на пересечении полки со стеной, то координата деления любой точки равна нулю ( z=0 Л —
Момент инерции отдельных элементов их изгибных центров; 2, J2, g, L, z-момент инерции отдельных элементов сечения относительно оси симметрии z\2,\8, C2? 8-расстояние между центрами изгиба соответствующих элементов Людмила Фирмаль
1 и 2, 2 и 3, и т. д. Эти уравнения были использованы для определения центра изгиба и веерообразного момента инерции двутавровой балки. Пронумеруйте полки и стены, как показано на рисунке. Для 496 начальных точек возьмите центр изгиба верхней полки (I). Игнорирование собственного момента инерции стенки относительно оси Z、: L, GS B1+L, 2C3, 1 _ L, 2^3,1 Jz~L’ Jz=2J8) Zt и расстояние c8j i=h, поэтому az= -. Момент инерции секции по формуле(30.47) рассчитывается следующим образом: (po-^1, (O==:^2, (O==L, (O==0))). j_L,2^1,3 _ _ Цзи, Ж_ З^2, Л7 2′ 1) б у Ч К О В Д. В. И М р о щ и Н С К И Й А. К., кручение металлической балки,§ 24.§ 181] пример 569 расчет характеристик сектора Потому что… Это то, что ранее было получено другим способом (Формула (30.44)).
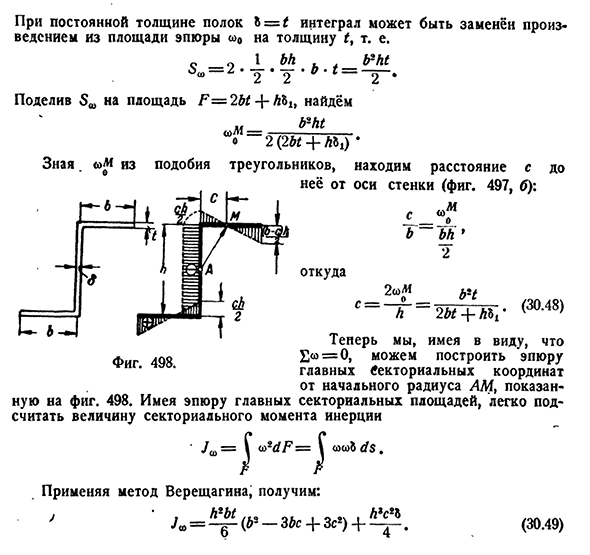
Формулы(30.46) и (30.47) представляют собой композитный профиль, состоящий из элементов с заданными характеристиками расщепления на столе Ост (заклепки и сварные балки, прокатные профили, армированные листами и др.). 6) рассмотрим другой случай в разделе несогласных Z(рис. 497). Центр тяжести секции o находится в середине высоты стены. Главные центральные оси инерции y и z наклонены под углом a к соответствующей линии контура сечения. Для определения положения центра сгиба и основной нулевой точки сектора возьмем точку A и построим вспомогательный участок площади сектора<O0. 497, род. Для определения координат центра изгиба графоаналитическим методом Верещагина строится график расстояния точки контура поперечного сечения главного шпинделя ywz. Для точек 1 и 3 профиля значения координат y t;
z t и y t следующие: х Зі=23=+г п о с Аналогично, для пунктов 2 и 4、: потому что Соответствующие графики y и z показаны на рисунке. 497, В и Д. Оба сюжета были антисимметричны. Таким образом, сумма произведения<O0 Y dF и z dF изменяется на ноль, то есть секторно-линейный статический момент становится равным нулю,^=0 и VG=0, а центр поперечного изгиба выравнивается с центром тяжести. Чтобы определить местоположение главной нулевой точки, используйте следующее уравнение(30.41): База Gde570[гл. XXX Из-за постоянной толщины полок b={целое можно заменить толщиной t изделия с площадью участка o) 0, т. е. Q9 1BH h b2ht g=2&4-l & b search=_ _ _ b* _ _ h_t_ _ O2(2bt+hbi) треугольник, то Знаю, сходство с м Отчет Найдите расстояние C до оси стены(рис. 497, Б): М. б~б ч’ Откуда Два. 2 «+L «x’(30, 48) здесь мы можем построить координаты главного вектора от первого радиуса AM, показанного на рисунке, имея в виду, что£<o=0. Используя график 498 основной площади, легко вычислить значение секторного момента инерции• / W= = Y w2d F=^Qtobd. Около
Смотрите также:

