Оглавление:






Примеры вычисления напряжений в тонкостенных стержнях
- Примеры расчетов напряжений для тонкостенных стержней. П р и М Е Р р 117. Тонкостенный стержень желобчатого профиля, прижатый одним концом к стене), крутящий момент Mo=6KGM. Найди Вели x) в крайнем случае предполагается отсутствие истощения. Степень тангенциального и нормального напряжений в опасном сечении стержня, размеры которого приведены на рисунке. 501:/=1 м; н = 200 мм; Б= = 100мм; & 1мм. Для решения этой
задачи необходимо сначала найти значения геометрических характеристик сечения. Поперечное сечение L=(2^4-L) & =4cm2. Фигура. 501. Расстояние центроида сечения от оси вертикальной стенки: Бакенбарды= 2м2 2 • 10 • 0,1 F-4 Пять. — =2,5 см. Момент инерции сечения относительно главной центральной оси: =+ = г № 7, ноябрь. =2 Рут — + — г с^J в Y и У2=41, 7cm4. 574 база[гл.
XXX К —- Используйте формулу (30.42), чтобы найти координаты центра сгиба: Людмила Фирмаль
_ _ _ 3 — 10* — 0,1 _ +(6 * lO-f-20 • * 0,1-постройте координаты сектора. 502), значение которого равно: ф Очки за 1<•>!== — <0| = —-a-J=i———3-,-7-5— — −2—0- = — 37,5 cmt, точка 2. Момент инерции сечения секции (по формуле 30.43):,_ _ b * h4 2h&+3bt_ 10* • 20* • 0,1 (2 • 20 4 -3 • 10) _ o p o l l (0-12 * 6^4-L Ватт- 12(6 • 1 0 4 -2 0 ). 0,1′ Крутящий момент инерции секции= ’10 + 20) • 0,1′ «»0,0133 ссылка. Статический момент максимального сектора отсеченной детали (см. формулу 30.43′): e(b-A t f h b(10-3. 75)».2 0-0, 1 1л л. Шах.——= ———— 19,6 ссылка. Торсионно-изгибные характеристики стержня:• «K S= / S S=<» o o o i3 2+a/ = 0,00132 • 100 = 0,132 < 0 ,5 (§177). Из-за очень низкой жесткости при чистом кручении(GJK) можно оценить, что внешняя нагрузка
прекрасно воспринимается стержнем только по изгибам полок и стенок. В этом случае димер изгиба-кручения в пинче может быть определен на основе аналогии, упомянутой в конце§177: max£L40 / =600.100=60000 кг см. Чтобы знать методику точного определения дифференциального уравнения (30.29), мы ее выполняем. Что такое внешний момент Af0=const?Т= = 0, d х’ Рассчитайте эластичность Имейте в виду, что общий Интеграл уравнения (30.29) равен B=. КЛ Ш А х+c8ch Ах. (30.57) любая интегральная постоянная определяется из условия фиксации конца стержня. Зажмите в X=0O’=0. Таким образом, ноль — это момент чистого кручения M K, поскольку 6’= = 0. S s L4K4-
- это условие может быть записано отдельно;1) p ri l:=0^=M a=Ml;§183] пример расчета напряжений 575 2) Когда x=Z Z? =0.(Это следует из состояния беспрепятственного истощения свободного конца стержня). Подставляя эти условия в Формулу (30.57), x=0jT=Cia chO+Ci a sh O=Afo, откуда М СЈ=~;Х=З Б=CishaZ+CiChaZ=о, г Откуда С,= — C1th а/= — ^т ч а/. Присвоение значения любой найденной константы(30.57) приведет к B=^~(s h A x-thaZchax). Когда x=0 max V= — ^t h a/. От%=0,00132, th aZ=th 0,1, 1 32=0,131, то максимум= — = «- М » •100=60 000 км см. Изгибающий момент того же сечения, как показано, выглядит следующим образом: tahl4sh=L4o=-ООО кгсм. Теперь перейдем к определению стресса. Нормальное напряжение максимального участка опасного участка возникает в крайней точке полки (т. е.>2 и 4, фиг. 502): а£L?=»>»»<±Д=±, 280 SPT40 2920. Тангенциальные сектора подчеркнуть: тах Т_ М Л600•/гг/Си *
Т А Х Т» — Д У;-2920. OD4 0Kg1sm * П Р и М Е R118. Определите значения нормальных и касательных напряжений в опасных сечениях стержня, которые рассмотрены в Примере 117 е IB7 Л * 4 Он расположен в главной плоскости выхлопного газа и нагружает его парой сил, равных A40=100KGM(чистый изгиб, фиг. 503). Предположим, что момент L1o образован парой поперечных сил. Г с=2,5 см; Ай з = z3jb см; дя=266tl см;)2=4\, 1cm4;/<о=2920cm; / к=0. 0133cm4;inaxSM=19,6 см’;/=1 0 0 см; а=0.00132^;а=0.132^; а/ = 0.132. Приложенный против центра изгиба сечения контрэксцентриситет (плечо) (рис. 503) E=Us+ » u=2,5+3,75=6,25 см. Основание[гл. XXX Формул
у для коэффициента силы приведем в таблице и примем согласно таблице 27 (§ 177). Людмила Фирмаль
Ch изгиб и кручение бимомент G Ah; In=In (x=/in) Max. Принятый в таблице знак минус заменяется на плюс (см. таблицу 27, Схема 3), так как эксцентрик е переносится на противоположную сторону. Изгибающий момент М Е==А * Ш Ач; Schach = amoe * й/(х=/). Согласно этим данным, цифра. 504 участка встроены, и L4K; вычислить максимальное число: крутящий момент MK= — = — aMQe sh Ah ch al’ Максимум в=10 000•6.25=62 500kgslg\Макс= 1000 • 6,25 • 0,00132 • 0,131 = 10,8 кгсм \ Макс L4K= Макс=-10,8 кгсм. Опасное сечение (свободный конец стержня) получает наибольшее значение в точке 2(Рис. Пятьсот два): ^Дж^МАКС / в* » макс=—————-г — =(- 10000I-10)>5 0 0.6 2,5 АПАП — Нормальное давление Касательное напряжение: а) от изгибающего момента б) крутящий момент от L U_10, 8-0, 1 Js~0.01333-z•как и в предыдущем примере, нормальное напряжение сектора (зола= = 1340кг!(см) * секторное
касательное напряжение всегда мало и может быть проигнорировано. Тангенциальное напряжение из-за чистого кручения также невелико. Однако он может достигать очень значительных значений, как показано ниже. П р и М Е Р119 двутавровая профиль нет. Балка с пролетом 206 (ОСТ10016-39) 1=4 м, эксцентриситетом Е=3 см (рис. 505). На концах балки невозможно повернуть сечение относительно нейтральной оси, но с учетом возможности разрушения, расчет максимума в опасной части балки,§ 183], например, 577 напряжений.
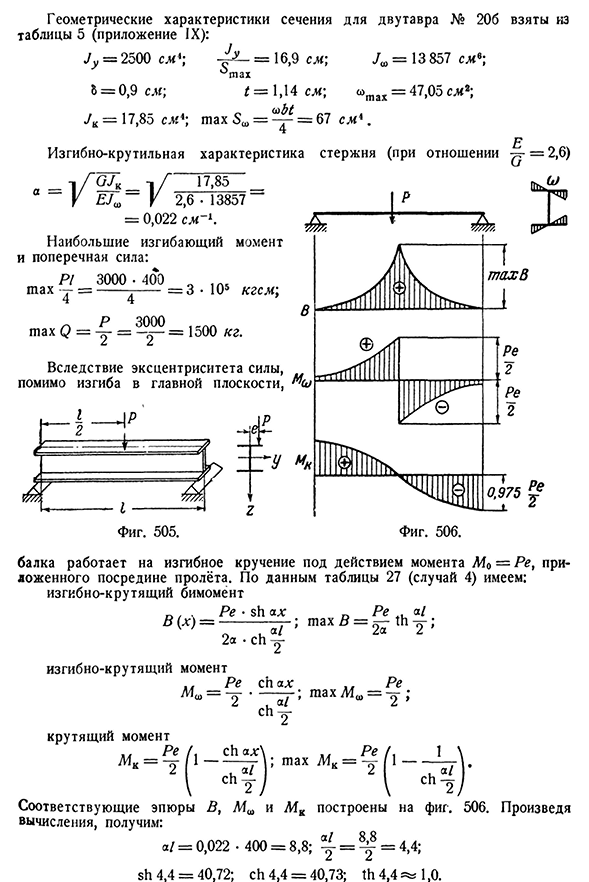
Я думаю, нет. Геометрические характеристики поперечного сечения для 206 взяты из таблицы 5 (приложение IX): Jy=2500cm*; Ja=16.9 cm; Ja=13 857cm9;^tah5=0.9 cm; t=1.14 cm; x=47.05 CM cm2 Е Изгибно-крутильные свойства стержня (в соотношении=2,6)_ — \f17, 85_ _ y к 2, 6. 13857″=0,022 см-4. Самый большой изгибающий момент и поперечная сила: Макс П—1 = −3-0—0—0—-4-0—0= z o * 101A5, кгсм;4 4′ п P3000 Для, Макс Q= — = — =1500 кг. В дополнение к изгибу в главной плоскости, для эксцентриситета сил, Фигура. 505 рис. Луч 506 приложен в середине пяди при работе изгибающего кручения под действием M Q=Pe. Согласно таблице 27 (случай 4) мы имеем: изгиб и кручение бимомент п. Ре * Ш А Н ре.. А/=м а х B=^т г;2а. ч г Изгибающий момент ре ч а МШ= — г Ре Но / ТГМ = −2; ч т Крутящий момент Re-d ch x. Re D1 \ Соответствующие графики B, M W и M K представлены на фиг. выполните 506 вычислений, которые собраны в: а/=0.022•400=8.8;г=4.4;sh4. 4=40,72; СН4. 4=40.73;тн4. 4= » 1.0. 19Н. М. База Belyaev578[ГЛ. XXX Если мы подставим Ch и th в формулу
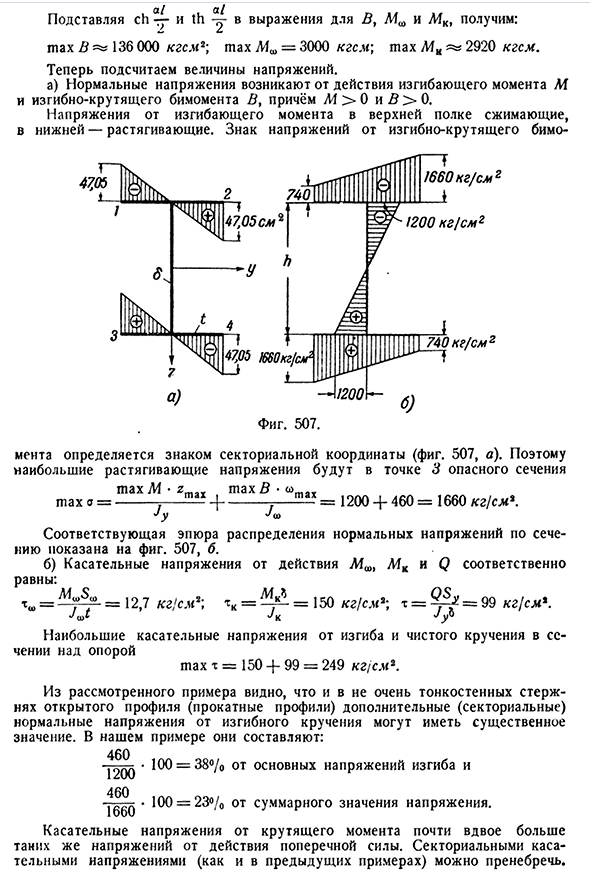
для B и L4K, мы получим до 136 000K gem2; Max=3000K gem; Max L4K2920kg cm. Теперь давайте рассчитаем величину напряжения. а) изгибающий момент M и изгибающий момент бимомента B, причем под действием M>0 и B>0 возникает нормальное напряжение. Напряжение от изгибающего момента верхней полки было сжимающим в Нижнем напряжении. Признаки напряжений от изгиба и кручения Bimo Мента определяется знаком координат сектора фиг. 507, а). Таким образом, максимальным растягивающим напряжение
м будет точка 3 опасного участка rn ax A f-zmaT m ax5-o max a= ———- — -|———- — — = 1200 + 460 = 1660 кг / см. Это позволяет определить нормальное распределение напряжений относительно площади поперечного сечения. 507, б) касательное напряжение под действием MK и Q равно соответственно следующим:=f f f=12,7 кг / см2;=f! =150кг / см2; г= = 99 кг! см Максимальное x = 150-f-99=249kg / cm2 поддержки Jyu самое большое напряжение сдвига от гнуть и чисто кручения в верхнем разделе. Из рассмотренных примеров следует, что в очень тонкостенном стержне с открытым профилем (прокатанный профиль) необходимы дополнительные (секторные) вертикальные напряжения, обусловленные изгибным кручением, в данном случае 460. —. 100=38 от основного напряжения изгиба% Четыреста шестьдесят. Тысяча,
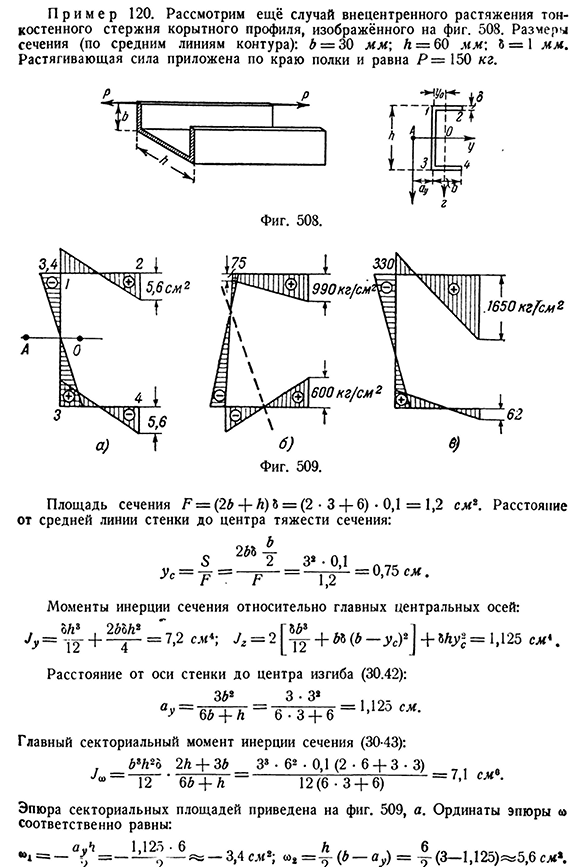
шестьсот, шестьсот 100=23% от общего напряжения. Тангенциальное давление от крутящего момента почти в два раза больше давления от действия поперечной силы. Касательное напряжение сектора (как и в предыдущем примере) можно игнорировать.§ 183] пример расчета напряжений 579 П р и М Е Р120. Рассмотрим также случай центрального удлинения тонкостенного стержня желобчатого профиля, как показано на рисунке. 508 размеры сечения (по средней линии профиля): b=30 мм; A=60 мм; B=1 мм, усилие растяжения добавляется по краю полки, равное P=150 кг. Поперечное сечение F= = (2b+h) b=(2 • 3 + 6 Да что с тобой такое? 0,1=1. 2cm2. Расстояние от средней линии стены до центра тяжести секции: S2M T32-0. 1P7S Us= — R=R= — ^’=0.75 см. Момент инерции
сечения относительно главной центральной оси: J. y=S1AT3+~2H~14H ~ 2=7, O2m ’ j z = =2[T T+I W / a-Us>H2]1+I * h y’O~1, 1Y2K5 Расстояние от оси стены до центра изгиба (30.42): 3ft2_Z-Z2 / OH-6ft+ / G— 6 — 3 + 6 -«около 2 см» Главный сегментный момент инерции секции (30-43): J a, ft8ft2o2L+3ft_Z8■ 62 ■ 0,1 (2 • 6 + 3 • 3) — ,l~12 ′ 6ft+ & — 1 2 (6 −3 + 6) —’ J C — * — график площади сектора показан на рисунке. 509, a. вертикальные оси графика равны: «1= — 3,4 p. I2;=A (ft-AU) = y(3 −1,1 2 5 )^ 5,6 см. 19 * 580 изогнутый стержень[гл. XXXI Максимальное нормальное напряжение возникает на краю растянутой полки и равно следующим значениям: Я P\M Ug\I V< * a max I = p T » t «I/» I/’ Один. J y и Куда? л
Смотрите также:

