Оглавление:
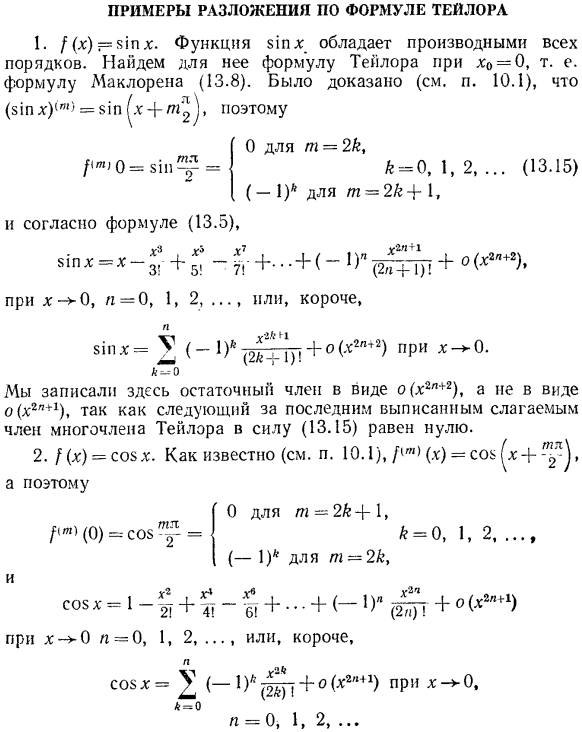



Примеры разложения по формуле Тейлора
Примеры разложения по формуле Тейлора. 1.F(х)= 51px. Функция zx x имеет производные от всех orders. (13.8). она была сертифицирована (см.§ 10.1) (81пх) (ш) = 81п ^ ^ + Т2^, таким образом По формуле (13.5)、 x-0, u = 0, 1, 2,…в случае, или короче.
To для этого мы находим формулу Тейлора для x0 = 0, то есть уравнение для Маклорена. Людмила Фирмаль
- Здесь я описал оставшийся член в виде o (x2n + 1), а не o (x2n + 2), потому что член полинома Тейлора рядом с последним членом, записанным в (13.15), равен нулю. 2./(x)= const как известно (см. раздел 10.1), fw (x)= cox +、 И так оно и есть.、 he-0 n = 0, 1, 2, … In, or, короче говоря、 3.!(Х)= ех. (экс) (Н-Экс, на следующей/ ЛН) (0)= я, П = 0, 1 x-0, n-0, 1, 2, или, короче говоря.
- Поэтому, если вы замените x на-x, это выглядит так. Сложение и вычитание(13.16) и (13.17), мы функций sx и cbx. 5. f (x)=(1 + x) r -, а a-фиксированное число. пн (х)= а И так оно и есть.、 6. /(х)= 1П(1 + х).
В силу единственности представления функции в указанном виде полученные соотношения являются формулами Тейлора. Людмила Фирмаль
- Легкий для понимания x-0, n-0, 1, 2,…Или короче говоря、 И вообще/ (*) (x)=(-1)#-1(&-1)! (1 + l) й, k = 1, 2, таким образом Замечание. Из-за следствий теоремы 1, полученную формулу можно записать следующим образом, используя символ O (O large): Запись выражения Тейлора в некоторых вопросах более удобна, чем запись с символом o (o small).
Смотрите также:

