Оглавление:



Примеры расчётов при косом изгибе
- Пример расчета косого изгиба. П р и М Е Р105. Пролет обрешетки (расстояние между фермами) равен/±=4LH, угол наклона кровли к горизонту 25°; нагрузка от снега и перекрытия собственного веса равномерно распределяется при прочности q=400 кг.)см2. Максимальный изгибающий момент L4t a x становится центром
пролета.. q l2 400•16ALL^Shah=V= — g— — — =8 0k™ — угол CP равен наклону крыши, то есть 25°, поэтому из Формулы (26.7)и условия h]b=2: (П О с? + Грех(0,906 + 2 • 0,423)=1402с м \ Следовательно, h j/1 2 — 1402 =25.6 B с 26см = 13см. Самый большой прогиб клеть находится в середине пролета. Момент инерции секции равен, b № 1 3-2 6
3 1O L_L.. b * h13s-26. Да.= » —— 12— = 19 0 5 0 м и= — — — — — =4760 см. Угол Людмила Фирмаль
наклона нейтральной оси a определяется условием tg a=Tg CP^=tg2o°•=1.86 o и поэтому состоит из A = 61°50 ′ и плоскости изгиба с плоскостью внешней силы.= 61° 50′ — 25° = 36° 50′. Прогиб плоскости максимальной жесткости выглядит так зет 5s?4кос Ср 5 • 4 • 44 • 10s0, 906_Yy W W y E384 ■ 19050-10s-0, m CM§ 159] пример расчета диагонального изгиба 493 Полное отклонение равно/ = — ^ — = ^ ^ = 1,35
смотреть J cos a0, 472y осевое отклонение (параллельно стороне B) равно/y= / z tg a= 0,6 4 −1,8 6 5 = 1,19 смотреть Поэтому, если принять во внимание, отклонение направления оси OU намного больше, чем направление оси Oz и приблизительно равно общему отклонению. Результат расчета напряжения- П р и М Е вечере r106. Размеры углов 160×160×16 мм служат балками, шарнирно закрепленными на обоих
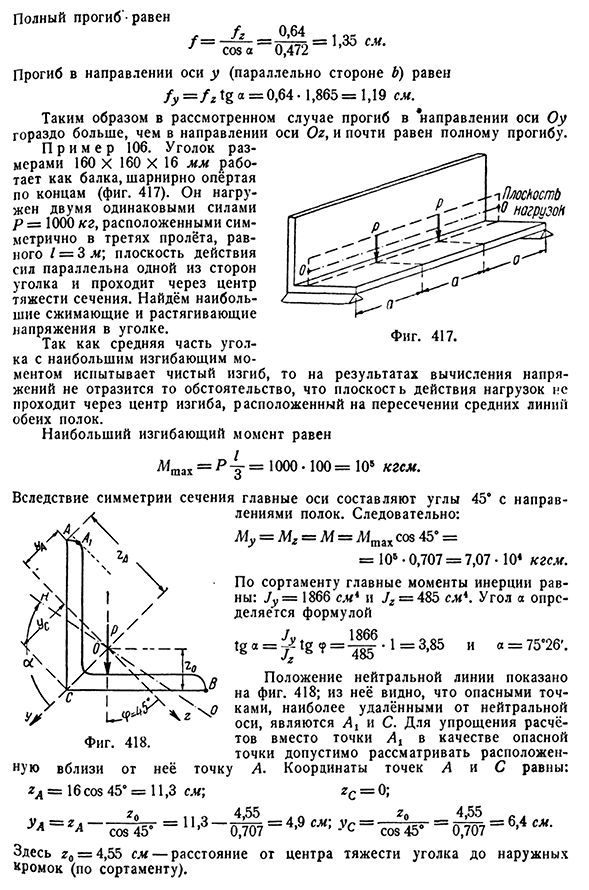
- концах(рис. 417). Она нагружается двумя одинаковыми силами Р=3 кг, симметрично расположенными в двух третях пролета, равного Z=1000м\рабочей поверхности силы, находим максимальные сжимающие напряжения и растягивающие напряжения на углах, параллельных одной из сторон угла. Центральная часть уголка с наилучшим изгибающим моментом испытывает чистый изгиб, поэтому рабочая поверхность груза расположена на пересечении средних линий обеих полок и Центра изгиба. Максимальный изгибающий момент будет равен Afmax=P y= = 1000 * 100=105kgsm.
Благодаря симметрии секций, главной осью является угол 45E, который имеет направление на полки. Таким образом, му= = м = АФМ axcos45°=10В * 0.707 = 7.07 * 10 * кгсм. В соответствии с этим диапазоном основные моменты инерции равны: Jy=1866 сми=485 см. Угол a определяется по Формуле= = 1=3,85 и a=75°26′. Положение нейтральной линии показано на рисунке. 418; затем от нейтральной оси вы обнаружите, что самые дальние опасные точки-это/It и C.. l — * cos45° » 11 1, O3 04J, 5057-4L, 9L s m; U C-cosz Q4 5°-04,, 75057 6s, 4. Здесь?0=4,55 см-расстояние от центроида угла до внешнего края (по градусам).494 косой изгиб[гл. XXVI Напряжение определяется по формуле Для точки А напряжение от обоих изгибов
представляет собой сжатие• * l= — ’ ■ «’ ■i o’G®+= — 1W Там будет растяжка в точке C AU=+7.07 * 104=+933 кг! см3 Так как точка С находится на оси Людмила Фирмаль
инерции, то второй член уравнения напряжения равен нулю. П р и М Е Р107. Стержень зетообразного сечения пролетом 7=3 литра; он нагружен равномерно распределенной нагрузкой 4=50 0 км! м\размер Для ЛЛ\ л; В В Фигура. Четыреста девятнадцать Поперечное сечение и положение грузовой плоскости показаны на рисунке. Основной момент инерции секции 419 составляет Jy=2765cm4, J2=160 см * \угол, образованный максимальной жесткой поверхностью с Дзета-стенкой, равен 18°. Толщина стенок составляет 1 см. Найти максимальное вертикальное напряжение и максимальное отклонение. u l Yal qP500-Z2 самый большой момент tahm= -^—= — —- = = 562 это было так давно. У=СР=18°, то Sin=0.309; соѕ=0.951. Положение нейтральной оси определяется отклонением от оси Y на угол a: tg»=tg _ все Г°^5 1 ’9,36, 0,309 • 3,57 1 — ± 5 Б2 0 ° [» 2765 + —— 1 6 0 ~ ] = = ± 56 200 [0,0032 4- 0,0069] = ± 568 кг. Отклонение в направлении оси Z выглядит следующим образом ф 5^ / 4cos п < — г—0.52 см.
Смотрите также:
| Косой изгиб. Вычисление напряжений | Изгиб балки при действии продольных и поперечных сил. |
| Определение деформаций при косом изгибе. | Учёт деформаций балки |

