Оглавление:












Примеры расчётов на ползучесть
- Пример расчета ползучести. П р и М Е Р145. Стержень, который изготовлен из хромомолибденовой стали и имеет площадь поперечного сечения F=2C x2, растягивается силой P. Определить предельно допустимое значение силы Р в двух вариантах: 9 м л и Н Н Н. основы расчета на ползучесть, 1948;К А ч а-н о Л. М.,§ 257 теории ползучести] пример расчета на ползучесть 807 Температура 7=480°и T2=650°, срок службы стержня = 5000 часов. Максимальное значение равномерной относительной скорости ползучести не должно превышать [t>n] = 6 • 10~7 • —. Коэффициенты запаса
прочности, относящиеся к пределам длительной прочности, принять равными^=1, 7. Для стержневых материалов установившаяся скорость ползучести может быть рассчитана по формуле vn= / gap, и ——-2)=~~б’ /т0^ И они представлены в таблице 44. Предел длительной прочности-значения коэффициентов K, N, а Т а б л и Ц А44. Значение коэффициента. Температуре г°н Второй л — — — ЮЖД — — — — кг время Но б 480 8.35 — 0, 58. 10-30 4,2 0,15 650 3.25 0.17 * IO — * 8
Один. 2,3 0,25 Решение. Допустимое напряжение для допустимой скорости Людмила Фирмаль
установившейся ползучести определяется по формуле (39.9): [’]==И • Температура T при T=480°: И при температуре 7=650°: Допустимое напряжение на пределе длительной прочности определяется по формуле е Футболка * При температуре 7’1=480°имеем: E4′ 2 66,68 K d i-1 7. 50000-15-я) 7. 3,588-1 0,9 3К г! м’* А при температуре G2=650e:^2,3 9,974 [°Б<К-1)7. 50000,2-я>7 8,409″0,7 0К г m1m *- 2 основание e808[гл. из расчета на 6 ползучести. XXXIX Результаты расчета показывают, что температура 7=4de[a]1[aBJ2. Так, в первом случае допустимое напряжение должно быть равно[a] x=752 кг/см2, а во втором случае — [AB/] 2=70 кг / см2. Допустимая сила
равна[P]=F[a]=2 [St]. При температуре t! =480°[P]i=2 * 752″=; 1500кг; и T2 = 650°[P]2=2 * 70 — =140кг. П р и М Е Р146. Для определения частоты предотвращения утечки пара необходимо определить температуру, при которой будет работать фланцевый соединительный болт паропровода, если начальное упругое натяжение каждого болта (Р=3000 кг) не должно быть уменьшено более чем на 40%, Т=425°. Сечение болта L=3cm2; материал Болта-углеродистая сталь£g=1,77•10 ′ ®кг[см2 (T=425°), установившаяся скорость ползучести, уравнение v n=N при T=425°k=2,26 * 10-25cm2p! Время КГП, и Р=6. Эта задача
- решается в предположении, что фланец паровой трубы абсолютно несжимаем. Решение. Когда фланец трубы пара совершенно несжимаем, вся деформация первоначально протягиванных болтов (затягивая), с течением времени ползучесть потока, упругая деформация Болта Д/и постепенно войдет в пластическую деформацию д/н; должный к этому, давление Болта будет уменьшено. В то же время Или Д / Г/П=ад) — константный Где A0-начальное упругое напряжение Болта, a-напряжение в момент времени t, EG-модуль упругости материала при заданной температуре T. Проигнорируйте переходную фазу ползучести и замените SP, чтобы получить такое дифференциальное уравнение: Или £ = E ТК-Д-т. Если мы интегрируем это уравнение Один. (П-1) an_1—Е Т Т 4″С(а) Где C-интегральная константа. При t=0a=A0 / t§ 257] пример расчета
ползучести 809 Если присвоить значение c найденному выражению (a), то получится выражение, связывающее a и t: _50_______ Один. Используя численные данные, о которых идет речь, мы имеем: Трехтысячный. 1 | (6 — 1). 1.77•10Е-2.26-10-25 ^ооочень-1 Один. Тысяча. Один. (1 4 −2 • 10-3 — около 5 Или Т а б л и Ц А45 З Н А Ч Е Н И я т Ст в кило! См. t (единица измерения времени) Но В 1000, 0, 0. 900 347 335 800 1026 960 700 2475 2230 600 5930 5000 500 15500 11900 400 48300 31700 Значение t, вычисленное по последнему выражению, соответствующему различным значениям A, указано в таблице 45 (столбец D). Если натяжение Болта не должно быть уменьшено более чем на 40%, то затягивание
Болта должно производиться каждые 5930 часов или около 8,5 месяцев. Решение задачи релаксации напряжений в данном болте является очень приближенным. Из-за Людмила Фирмаль
пластичности фланца паровой трубы снижение напряжения Болта происходит намного быстрее. Решение этой проблемы несколько сложнее, учитывая пластичность фланцев. Не рассматривайте это решение, только то, что принесет ему конечный результат (см. таблицу 46)., Колонка C) упругая деформация фланца равна EY f-3 * 10 Поэтому, исходя из результатов более точного решения задачи, дополнительную затяжку Болта следует производить не через 5930 часов, а через 5000 часов или 7 месяцев. П р и М Е Р147. Круглый вал диаметром 24 мм работает при температуре T=540°, с постоянным кручением 7IK=20 кг. Материал вала-легированная сталь с модулем упругости G=6*105кг) см^(T=540°). Установившаяся скорость
ползучести может быть рассчитана по формуле T=540°k= = 2.5•1O~10cm2p! Время КГП и I=5. Найти распределение напряжения сдвига по поперечному сечению вала и углу закрутки после нагрузки 1000 часов. Решение. Предполагается, что гипотеза плоского поперечного сечения при кручении справедлива в условиях ползучести материала (это предположение очень хорошо совпадает с экспериментальными данными). Основа расчетов на 810 с половиной лет в данном случае[глава XXXIX Два соседних поперечных сечения вала, отстоящих друг от друга D x, оставаясь плоскими, вращаются с одной стороны только под углом dy к другой. Поскольку радиус сечения не искривлен, для относительного
смещения на расстоянии р от центра вала можно использовать известную (§ 57) формулу.: После нагружать вал, напряжение ножниц должное к ползучести материала постепенно увеличит; относительный угол закрутки также увеличит. Полная деформация сдвига происходит (У меня есть X В виде упругой деформации 7U и суммарной деформации ползучести 7P, т. е. 7-7U7P.: в=я ДТ д ДТ Д х * ДТ =4vy-ВН=Р Для упрощения решения этой задачи пренебрегают малым значением скорости упругой деформации
по сравнению с большим значением скорости деформации ползучести. Более точное решение этой задачи, учитывая g / y^0, чревато серьезными трудностями. Кроме того, мы игнорируем стадию неустойчивой ползучести и считаем, что получаем x>n=: Откуда Куда? 1-1 РП=Ф Р% Один. (И) (бел) [1г [К-Д-х * ДТ Дж Условия выравнивания момента внешней силы (крутящего момента) и внутренней силы упругости относительно оси вала записываются следующим образом: Где g-радиус вала. Маркировка 2+3n+1 Мы можем написать, чтобы принять во внимание(a)), ©§ 257] пример расчета ползучести 811 Поэтому распределение касательных напряжений по поперечному сечению оси при ползучести уже не подчиняется линейному закон
у. Если вы присвоите уравнению значения R=1,2 см и n=5, то получите 9Q1L и» ’ 4-1 J р п=^Вт-ч п р р■ 1,2 5 = 1,9 6 4 ’1,23,2 = 3,5 2 S М L’2- Расстояние p тангенциальное давление от оси вала равно: Тонны Двухтысячный. 3.52 Я — 1 Р5=568p5. В таблице 46 приведены значения t, соответствующие различным значениям R. значение t при упругой деформации вала приведено в той же таблице, рассчитанной по формуле.: L4K•R_2l4kr_2 * 2000~ ~ Jp~PG* «» 3.14 * 1.2 * p=614p. Благодаря напряжению ползучесть в сечении вала выравнивается, а на поверхности вала они несколько уменьшаются и их ось
значительно увеличивается (рисунок). 667). Т а б л и Ц А46. Значение т. Один. ₽ ₽ Я мм t исключение кг / см^ 12 737 589 10 614 568 8 492 543 6 369 513 4 246 473 2 123 411 Ноль. Ноль. Ноль. 0-0 200 300 400 500 600 700 600 Определяет длину блока. В (B) и © мы можем записать угол поворота вала: Критерий Д х ДТ Если мы интегрируем это уравнение в Т、 т+с. Д х ¥ Япония) i812 основа расчета ползучести[гл. XXXIX 1000= Предполагая, что это интеграл x-1cm、: Когда проблема данных Пирог 1^ \ Н \ Японский) 2000-2, 2 5. 1 0^9W5 6 • 105 • 3,14 • 1,24 \ 3,52′ =0,00102 4-0. 01480=0,0158 Р -. Отметим, что угол кручения вала при ползучести 1 см увеличивается почти
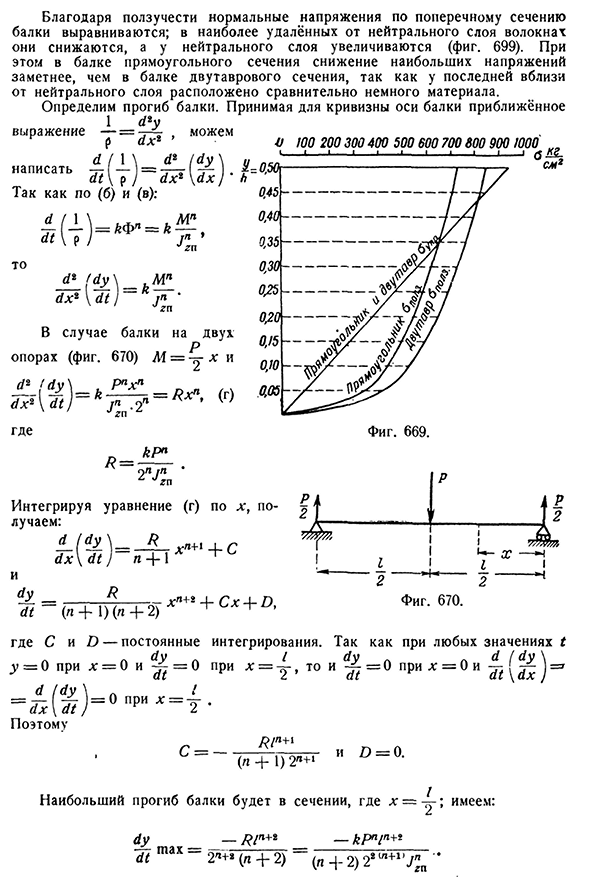
в 16 раз по сравнению с углом кручения при упругой деформации (первый член последнего результата), поэтому значительное снижение максимального напряжения сдвига вала не свидетельствует о том, что рабочее состояние ползучести улучшилось. П р и М Е Р148 балка длиной 50 см шарнирно закреплена на концах, а в середине пролета нагружена концентрацией Р=400 кг, работающей при температуре Т=500°. Материал балки-модуль упругости E=1,6(106 кг) см2, углеродистая сталь (при T=500E). Установившаяся скорость ползучести VN-KCN и T=500°k=1,5 1 0 ′ 15cm2 кг Y-I/g=3. Время Игнорируя стадию нестационарной ползучести, находим распределение регулирующего давления в опасном сечении балки и определяем наибольший прогиб через 10 000 часов после нагрузки. Рассмотрим два варианта поперечного сечения балки: прямоугольную и двутавровую (см. рис.. 668).
Смотрите также:
| Кривые ползучести и релаксации | Внешние и внутренние силы |
| Основы расчётов на ползучесть | Напряжения. Метод сечений |

