Оглавление:



Примеры расчёта статически неопределимых систем
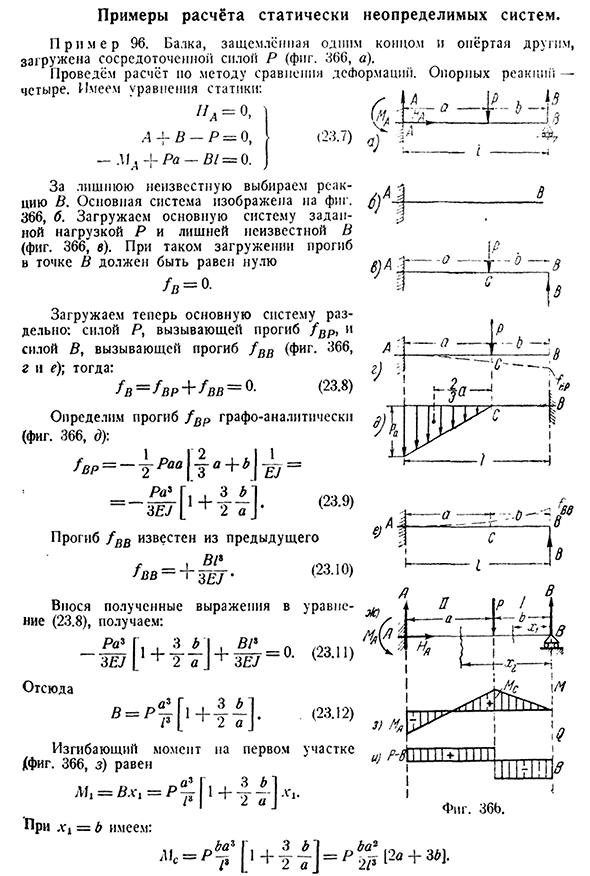
- Пример вычисления статически неопределенной системы. (2; П р и М ер96. Балка, зажатая одним конусом и поддерживаемая другим конусом, обладает сосредоточенной силой Р(рис. 366, а). Выполняем расчет методом сравнения деформаций. Реакция поддержки-четыре. У нас есть уравнения статики: д д-В-Р=0—L1D -} — РА-Я/=0. > Для дополнительной неизвестности выберите реакцию B, основная система показана на рисунке. 366, б. загрузите заданную нагрузку Р
и дополнительную неизвестную B в основную систему (рис. 366 в^). При такой нагрузке отклонение точки B должно быть равно нулю / V=0- Здесь мы ставим нагрузку на основную систему. 366, g и e); затем: =(23.8) (23.9)) Вы можете графически проанализировать отклонение (рис. 366, д):/л= — ±с.. / 1о+»/ — ± = РА * г,. 3-61 B отклонение/
известно из предыдущего f — ^ B1> Если мы введем результирующее выражение в nie(23.8)、: И так оно и есть. За вами./ Первый Людмила Фирмаль
изгибающий момент Cfig. 366, равный h) Когда HD=6 мы имеем: (23.10)) (23.11) (23.12) Сайт Уравнение- Фигура. 366.444 статический неопределенный луч [глава XXIII Для второго раздела-l»■ В=/мы имеем:^3Г, Боковая сила первого участка(фиг. 366, и равный: Второй В частном случае a-B=- Миллисекунды=+ П р и М EP97. Луч Рена конец а; конец АВ, Четыре. Я ньютон Но п 4 I Нагрузка усилием P (рис. 367), с упругой опорой (пружиной) упорного зажима. Это значение может быть вычислено по формуле (11.28) (§ 65).: — Я.
.. — Фигура. 367. И a~(7g4extra если неизвестно, выберите реакцию B между балкой и упругой опорой. Ход решения остается таким же, как и в предыдущем примере. Отклонение кромки балки B больше не равно нулю, но тяга пружины от силы B. Ze+Zee= — ^4(23.13)принимает положительное направление отклонения, поэтому знак минус ставится перед X. присваивая значения выражения(23.13) f,
- B p и F BB(см. Пример 96), значение X=AB: И так оно и есть. (23.14) Для абсолютно жестких пружин формулы a=0 и B совпадают с формулами, полученными в предыдущем примере (23.12). Определим максимальные напряжения балок и пружин по следующим числовым данным: I-балка № 20, J=1840cm4, W=184slt3, Pro — § 141] пример расчета статически неопределенной системы 4 45 л э/ = 4 м; А-B=2М; Р=2Т. Радиус витка пружины П=5 см, радиус штанги г=1 см, число витков П=6. Модуль:£ = 2-1 0V kg ’ cm2, (7=8105K G R m2, гибкость весны равняется:4 • 53 • 6 а » 8105•i4m/gвычислить отношение формулы (23.14) к реакции: 1+ Но £3/а 3 • 2 • 10″ • 1840 ■ 4 • 53 ■ 6 в— 2000 — 378/с
g-u43 * 10″•8 • 105 — W8 1 4-0,65 — 3 7 8 опасность представляет часть щипка и нижняя часть груза. Их первый MA=B1-P~ = 3 7 8 −400 — 2000 • 200 = — 248 800 кгс. А во вторых 43 * 10Е-8-105 И= Максимальное нормальное напряжение в балке равно|m axA f / 248 800 Т^= — 4_ Г8=1 3 4 3К г с м’- Максимальное касательное напряжение пружины 2BR2. 3785, сдвиг t= — y- = ——- — = 1200 кг см2. itr5~она — 1I33′ П р и М Е Р98. Нарисуйте момент в кадре. 368, а) под нагрузкой силой, r. жесткость стержня EJ постоянна. Когда мы показываем реакцию через L, N, MA, C, мы делаем формулу: n=P, A — \ — C=b, RA-Sa-MA=0. Основная система с усилием P и дополнительной неизвестной нагрузкой показана на рисунке. 368b Применяется теорема Кастильяно.
В Формуле для совместимости-O с вариантом f-d — Потенциальная энергия U Людмила Фирмаль
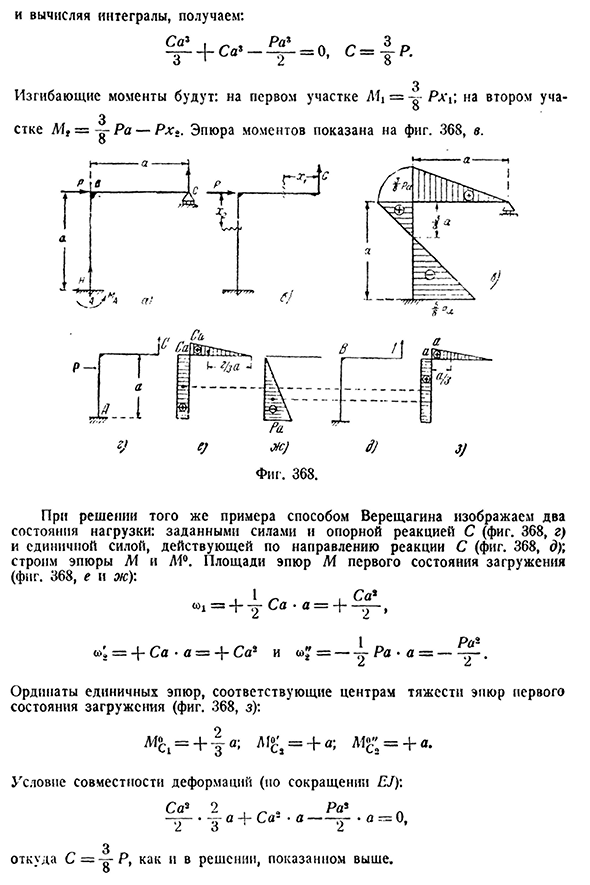
представляет собой сумму энергетической ценности первого участка SV и второй энергетической ценности A. формула/s=0 принимает вид yi1. 1-ый этаж, л. л е м д ДС Д х+Э J ДС Д х — ° ’ о Отчет Вычислите момент и его производные: = +C x lt—**1, — — y o u l L2, уравнение совместимости A C x F d x+(CA-P x2) A D x-0446 статический неопределенный пучок[CH. XXV Если вы вычисляете Интеграл: СА * 3 = 0, Изгибающий момент выглядит так: в первом сечении Ah= — g-RHC, во втором сечении M9~ ~ ^ — R a-RH*. Сюжет момента показан на рисунке. 368, ст. V9Ofc) / / 3) Фигура. 368. При решении того же примера метода Верещагина заданная сила и опорная реакция
(рис. 368, г) и единичной силы, действующей в направлении реакции (фиг. 368, f; участки M и D4°. Площадь участка М первого состояния нагрузки (фиг. 368, e и W)\ Вт, 1, х * я = т U СИА * а=н-у — , <4=+C e-e=+Ces и» ’ = — y RA■a= — вертикальная ось единичного участка (рис. 368, Ш): А^=+4а; L1C>+а; L1C=+»- Требования к совместимости деформации(согласно Эдж)\ СА * 2 РА2 •а+са * о * а=0, Где C=3 8P как в вышеуказанном решении.
Смотрите также:
| Выбор лишней неизвестной и основной системы | Определение деформаций статически неопределимых балок. |
| План решения статически неопределимой задачи. | Расчёт неразрезных балок. |

