Примеры расчёта кривых стержней

Примеры расчёта кривых стержней

• Пример расчета кривой стержня. П р и М Е Р 123. Вычислите круговое кольцо под действием двух сил Р(рис. 535). Радиус оси кольца/?(Поперечное сечение кольца Фигура. Пятьсот тридцать пять Часть его между секциями на секции а, считая МА, на и ниями А и тп через% ’0. Для этого отрежьте стержень в этом разделе. Этот разрез не делит

кольцо на две отдельные части, как в случае растянутого стержня, например. Эта проблема, как говорят, внутренне статически неопределима, несмотря на известную внешнюю силу,

действующую на кольцо. С другой стороны, если мы найдем напряжение, Людмила Фирмаль

действующее на какое-либо сечение, например D, и складывающееся в общем случае в пару Ma, нормальные и тангенциальные силы Na и Qa, то для этого нужно выбрать кольцо. 535) и воздействуя на систему Qa M, N и Q с Na для сечения TP, Qaa ppoollozhzhiitteellnyymmii и для балансировки указывая угол между сечениями-получаем: (31.42) Таким образом, задача сводится

к нахождению трех статически неопределимых величин внутренних сил в любом сечении кольца а: изгибающего момента Ма, вертикальной силы и вертикальной силы. Разрезать кольцевые участки точек А и С на две части(рис. 536), мы находим по симметрии, что нормальная сила сечений A и C равна P/2, а касательная равна нулю. Итак, из трех дополнительных неизвестных остается только

• усилие ма. Таким образом, четверть кольца AB можно рассматривать как свободный конец силоса, зажатого в секции B & кривой сердечник, загруженный в§ 196] И момент L4a; когда вы пишете, что вращение секции A равно нулю, вы придумаете условия для нахождения MA. (31.43) Где L4°=1-момент, приложенный к участку A в направлении неизвестного момента M a для действия. Изгибающий момент [формула(31.42)] равен М-р-2 (1 — п о с?) В дальнейшем, Л4°=+1 и DS = 7?насчет Ди. Если вы присваиваете эти значения выражению (31.43)、: l/2+L4a+u (1-COS<p) 7?О чем]/?о dtp=0. И так оно и есть. л/2л/2

4-й Ма Р М dy4* Или +Мало у+у/? ? г — ~РИ=0. И так оно и есть. Ма= — г-пра(1- = −0,182). Дж г(1-соз<Р)/?ГД? = 0, Отчет Изгибающий момент Ма был отрицательным. Теперь в разделе<p=te= — 2-Находим: Дж г М+ — Около В МВ=Ма±^Р Щ (- что?) == = −0.182 Р. 4-П Р0. 5. =4-0, 318 пр., p N b= — 2 cosccp=0. Поэтому кольцо равно нулю, в этом сечении есть обычная сила, но угроза поперечного сечения. П р и М Е Р 124. Чтобы найти изгиб фигуры. 537 изгибающий момент стержня и вертикальная сила (фиг. 537)под действием пары M, которая показывает реакцию на 7/d, L4l, A и B, составим уравнения статики: 2% = 0; T/A=0;£ / =0; A=B; £MA=0; VA+MA-M=0.608 изогнутые стержни [глава XXXI

Задача статически неопределима; для дополнительного неизвестного Людмила Фирмаль

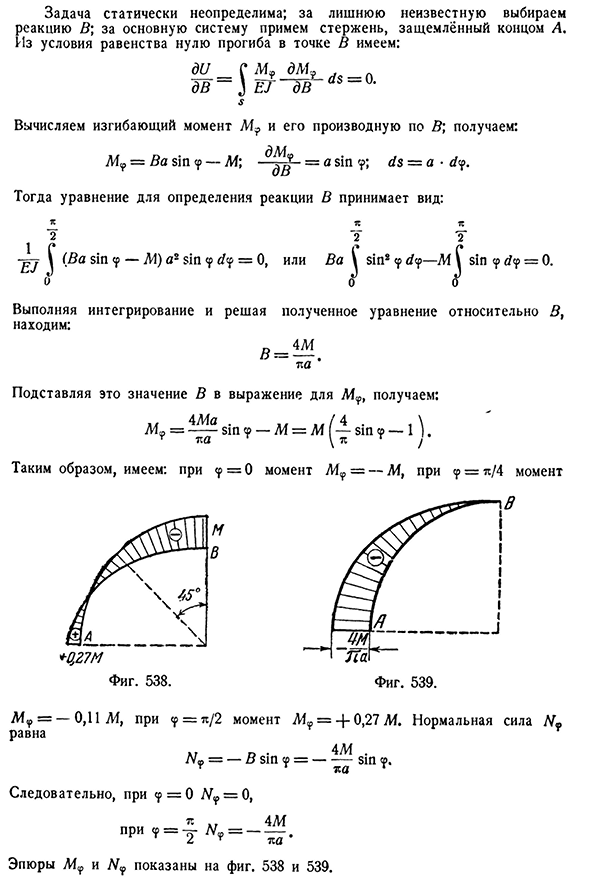
мы выбираем реакцию B; для основной системы мы берем зажатый стержень в конце D. Из условий, равных нулевому отклонению точки B, получаем: dU__с M<P DV-J EJ DV S ДС = б. Рассчитайте изгибающий момент A1? А по B его производным получим: M? =BA грех<п-Л4;ДВ= = в Sin<Р; ДС=а * г<п. После этого формула для определения реакции в принимает вид: Составьте Интеграл и решите найденное уравнение: Относительно, В Ссылка Присваиваете ли вы это значение выражению Af? , Получить: Следовательно, мы имеем:=0 момент L4? = — L4, CP = te / 4 момента Фигура. 538. АФ? = −0.11 Af,<P = te / 2 момент Af? =4 до 0,27 М. является нормальной силы в о•4Е1. Н= — грех СР в==——— грех Ф. г 7bea1 Следовательно, при<p=0^=0, p p и te kt4Af ? =у=^ — _ Участок A1<p и N? Показано на фиг. 538 и 539.

Смотрите также:

• Примеры решения задач по сопромату

Деформации кривых стержней	Расчёт толстостенных цилиндров
Вычисление деформаций с учётом кривизны стержня	Расчёт тонкостенных сосудов.