Оглавление:










Примеры расчетов при действии сосредоточенных сил
- Пример расчета Под действием концентрированной силы Рассмотрим некоторые проблемы, связанные с растяжением и сжатием. 1. Определите диаметр стержня с постоянной длиной поперечного сечения I=60 см(рис. 130). Материал стержня-сталь СТЗ, модуль упругости Е=2-106кгф/см2. Давайте также построим график X-смещения сечения стержня и определим изменение его общей длины. Этот стержень от продольных сил участка только 120преще. В крайних случаях наблюдается сила тяги A7=N / H=P-1200 КГС, в среднем сила сжатия L/n=2P=2400 кгс. Поскольку выступающий стержень должен иметь определенное поперечное сечение,
то последнее должно быть выбрано так, чтобы абсолютная величина силы, действующей на центральную часть, была больше. Представление напряжения в разделе этого раздела описывается следующим образом: «=F-F’P^1t2ic п*. 1___________ л ___ _ 1/3 1/3 — * X в SP X ППК Д Икс Или Откуда 2Р Ф Условия интенсивности просмотра Et Я p2R ^=0g0078cm СТЗ −0.0078 см рисунок. Сто тридцать. f> / oj * сталь [допустимое напряжение / SG] растяжение и сжатие одинаковы. Статическая нагрузка может быть под 10). Если подставить число, то получится площадь поперечного сечения стержня: Ф, ч. я…
я ж г г? Принимают равным 1600 кгс / см2(см. В- F>2 1S0 cm2=1>5cm2 И его Людмила Фирмаль
диаметр: д= Диаметр должен быть увеличен до ближайшего большого, принятого по ГОСТу. Вы должны взять D=14 мм (F=1.54cm2). Следует отметить, что расчет прочности на сжатие достаточен только для коротких стержней, особенно стальных круглых стержней менее 20. При сжатии же длинного стержня может произойти потеря сопротивления1. В нашем случае вышеуказанные условия для сжатой части маршрута выполняются. Давайте определим движение секции стержня. Например, мы условно фиксируем начало координат левого конца стержня (разрез а). Напомним, что смещение любого
поперечного сечения 1 отсчет сжатого стержня лампы указывается на CH, J9, 121 к исходной точке равно изменению длины стержневого участка между неподвижным и рассматриваемым участками. В первой секции переместите секцию, расположенную на расстоянии x от левого края стержня А-О; ОВ К(ч) — Когда Х= * О Я Когда X= — y На втором сайте Р4 — Она-3.2 • 106 • 1,54 см~0.0078 см. Я Икс= XW= п — =0,0078 см; Когда x= ~ g2~ / 1 С-1 К с=~эф Два. В третьем разделе-g-1<x< /, Схема перемещения показана на рисунке. 130 в этом случае длина
- всего стержня не изменяется. 2. Создайте график вертикальной силы, вертикального напряжения, относительной деформации и смещения ступенчатого сердечника (рис. 131). Стержень состоит из трех частей. В первом из них, на расстоянии x от неподвижного конца (0<x</), продольные силы, вертикальные напряжения и удлинение зависят не от координаты x, то есть положения сечения.: Рис сто тридцать один Перемещение сечения х от закрепленного конца стержня, Х(х) = ех== 4 пикселя Таким образом, смещение изменяется по линейному закону. В начале и в конце графика, если x=0, у вас есть следующие значения ^л= = 0; Когда x=Z 3.’ Аналогично, в следующих разделах(/<x<3Z) o _ _ _ _ _ _ e her’ Перемещение сечения
х от закрепленного конца стержня, 7L W EP • В начале второго раздела, x-I,. 4Р/ «3EF» L В конце раздела, x-31, Знак минус указывает, что рассматриваемый участок движется в направлении участка в начале координат. Третий сайт (31<x<4/) уу=р; о= Переместите участок, расположенный на расстоянии x от конуса D, P (x-31}ее В начале третьего раздела, В x-3/, В конце третьего раздела x=■41, Графики N, o, b и K показаны на рисунке. 131. График х позволяет определить изменение расстояния между любыми двумя
участками стержня, а следовательно, и изменение длины любой его части. Людмила Фирмаль
Определим, например, изменение длины второй части стержня. Для этого переместите последний раздел(раздел с) Лучший Солнце= п п 60, 60, 60. В начале раздела (Раздел B) вам нужно вычесть движение раздела. Результат,- 2P1, 4P1. 3EF3EF Знак минус рис 112 указывает на то, что длина рассматриваемого участка уменьшилась. 3. Проверим прочность ступенчатых стержней круглого сечения(рис. 132). Материал стержня твердеет из высокоуглеродистой стали с временным сопротивлением ov=9000kgf / cm2. Стержень растягивается с усилием P=8000kgf. Из-за резких изменений поперечного сечения стержня возникает концентрация напряжений. Поскольку закаленная сталь чувствительна к нему, испытание
на прочность следует проводить при самых высоких локальных напряжениях. Чтобы найти эти напряжения, необходимо знать коэффициент концентрации напряжений. Последнее зависит от отношения радиуса скругления к меньшему диаметру чернил 124g5 PJ в нашем случае-y — =0,25. Согласно таблице. 11 теоретический коэффициент концентрации напряжений a=1,2. Номинальное напряжение рассчитывается из меньшей площади поперечного сечения стержня: he= — F— = ——-= 2550 кгс / см2. * I. 2! Четыре. Максимальное локальное напряжение определяется по формуле (4.37): Дополнением=О0″=1.2 * 2550kgs/см2=3060kgs / см2. Прибыль Или °М<Х Для хрупких материалов при статических нагрузках, как уже говорилось, возьмем коэффициент / безопасность? Б=2.5 3. Запас прочности рассматриваемого стержня находится
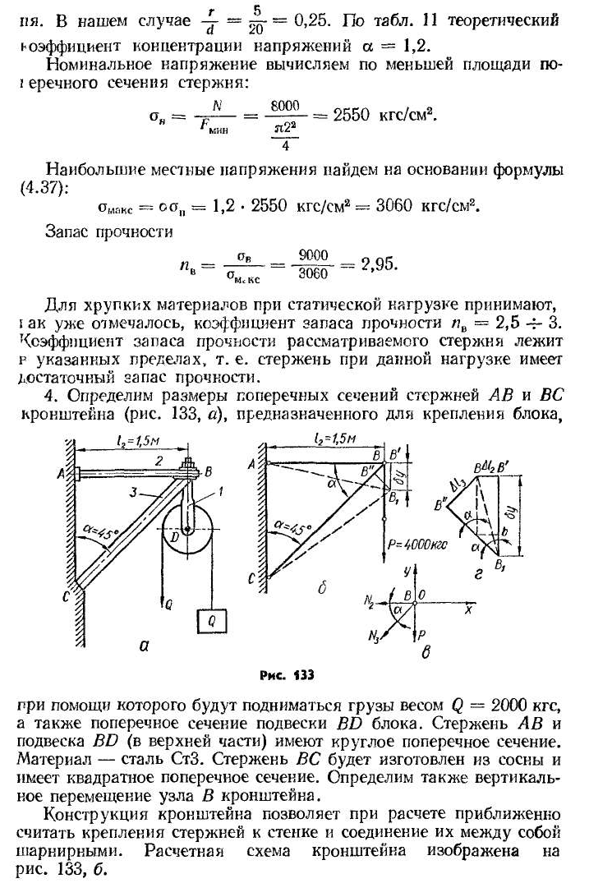
в заданных пределах*, то есть стержень при данной нагрузке имеет достаточный запас прочности. 4. Определите размеры поперечного сечения стержня AB и кронштейнов BC (рис. 133, а) для фиксации блока, С помощью которого груз весит Q-2000KGE, также поднимается поперечное сечение подвески блока BD. Стержни AB и подвески BD (выше) имеют круглое поперечное сечение. Материал-сталь СТЗ. Полюса Солнца сделаны из сосны и имеют квадратное сечение. Он также определяет вертикальное перемещение узлов в скобке. Конструкция кронштейна позволяет приблизительно рассчитать шарнирные их соединения друг с другом, учитывая стержни, закрепленные на стене. Конструктивная схема кронштейнов приведена на рисунке. 133, б. 125прежде просто определяет силу в узле подвески и равную ей силу, действующую на узел в — это
вторая ветвь троса, брошенная на блок. К узлу в кронштейне, и таким образом приложите усилие P=—4000kgs. Для стали СТЗ допустимое напряжение растяжения[о]= — 1600кгф/см2, для сосен допустимое напряжение сжатия fa_]=120кгф / см2. Модуль упругости для стали EO=2×10®кгс/см2,£d=10®кгс / см2 для сосны. Найти требуемую площадь поперечного сечения подвески BD. Нормальное напряжение подвески определяется по формуле Запишите условия прочности Где находится требуемая площадь поперечного сечения подвески п i_4000 м [о]1600′ =2. 5cm2. Определите диаметр подвески: dt=] L1,
13K2^=1,78 см=17,8 мм. Г Л Возьмем ближайший стандартный диаметр d=18 мм (F-2,5 4 см2). Поскольку предполагается, что стержни крепятся к стене, соединенной шарнирами, а нагрузка прикладывается к узлам (шарнирам), рассмотрим уравновешивание узлов (рис. 133, в), к которому приложены вертикальная нагрузка B и две неизвестные силы N2 11L^z, действующие соответственно на стороны стержней AB и BC и направленные вдоль их оси. При определении неизвестных сил в стержне обычно предполагается, что они растянуты и, соответственно, ведут вектор силы от узла. Знак плюс решения силы подтверждает правильность предположения о направлении силы, а знак минус должен заставить N2 и направить, как показано
на рисунке, предполагая, что на самом деле сила направлена в противоположную сторону и оба стержня сжимаются, а соответствующие стержни растягиваются. 133. Для равновесия узла B на плоскости сумма проекций всех сил, приложенных к узлам на координатных осях, достаточна, чтобы быть x 126II y был равен нулю. Направьте оси, как показано на рисунке. 133, ст. и далее… = — Az2-L’a cos a=0;= — P-JVgSin a-0. Следовательно, л^з=С-В — =- — — К Г с-5660kgf; Но У2 / 4000 • 2 / 2 п, п, п, п, п, п L; 2= — X3cosa=j кгс-4000 кгс, то есть стержень AB растягивается, а стержень BC сжимается. Из условий прочности стержня. о= — тг —
<Н G2 Определите необходимую площадь его поперечного сечения: P^9 4000 2O G. два. — 1600Х М» ■ S М • В этом случае она была равна площади поперечного сечения подвески. Так, диаметр стержня АВ должен быть равен диаметру подвески, то есть d=18 мм. Требуемая площадь поперечного сечения деревянных брусков. Г Г Ns5660 2 2Вт=[о_]=120С М=4 7С м • Квадратная сторона a-U с поперечным сечением 47 см=6,85 см. Округлите до ближайшего целого числа, возьмите== * 70 мм (F=49cm2). Определите вертикальное перемещение шарнира в кронштейне. Стержень AB удлиняется на величину ^2^2 ^С^2 4000 * 150 2 * 10E * 2.54 мм см=0,118 см. Бар сокращается на количество * 8/8 * Д * з 5660 • 1 5 0 /2 10 * * 49 см0. 245 сантиморганов
Смотрите также:
| Влияние различных факторов на механические свойства материалов | Учет собственного веса и сил инерции |
| Допускаемые напряжения | Статически неопределимые конструкции |

