Оглавление:




Примеры расчета статически неопределимых балок
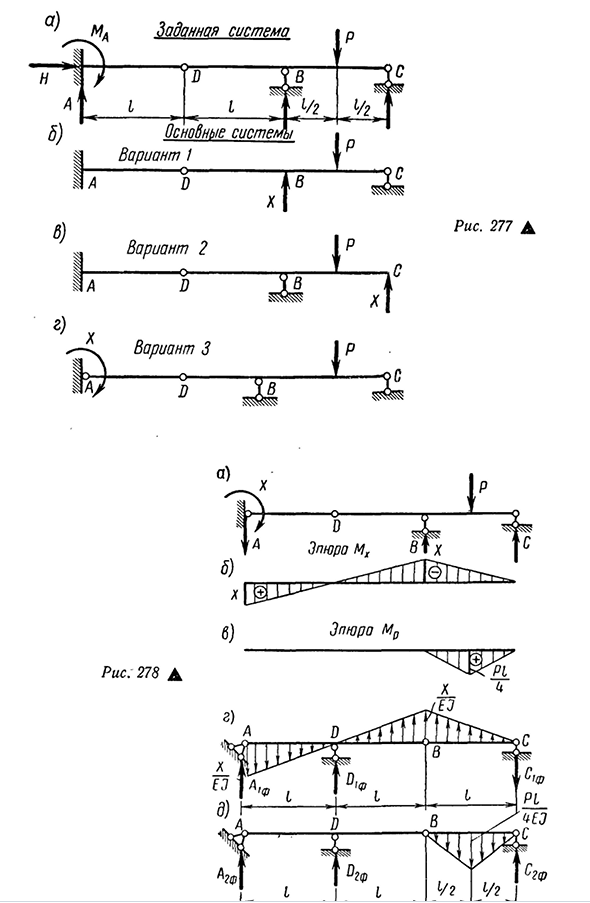
- Пример расчета статически определяемой балки Рассмотрим некоторые типичные примеры расчета статических неопределенных балок при изгибе. П р и М Е Р1. Статическая неопределенная балка с промежуточным шарниром O загружается в правый пролет концентрацией P(рис. 277.) Это требуется для построения участка M и (^. Эта система содержит пять компонентов реакции опоры. Для
определения этих реакций можно составить четыре уравнения статики: трехходовое уравнение статики (=0,=0 и=-0), которые являются общими и могут быть использованы для всей системы в целом. Таким образом, данная система некогда статически неопределима. Для риса. 277, b, C и
d представляют три варианта базовой системы. Вариант 3 принимается к вычислению. Уравнение Людмила Фирмаль
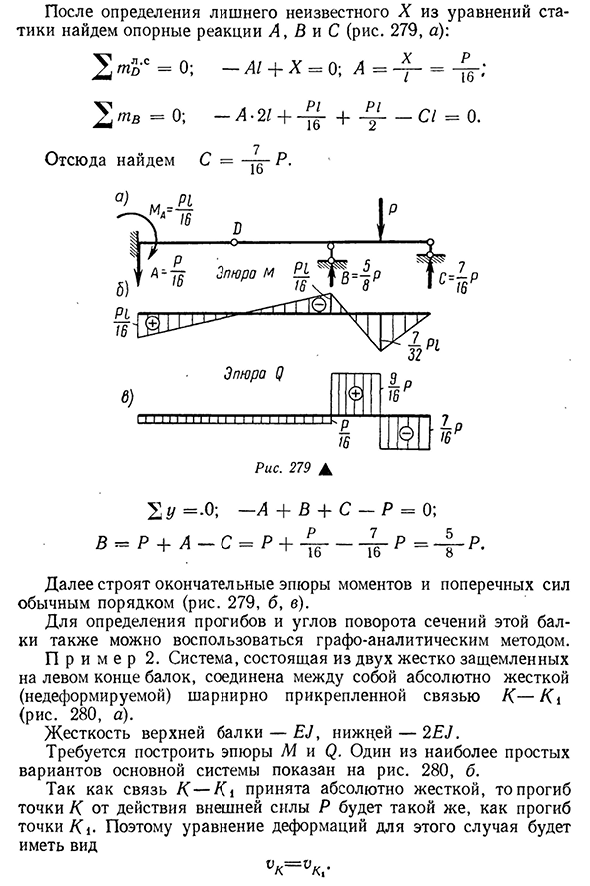
деформации в этом случае принимает вид 4>l=FDR+4>l l=0, (10.5).; 314fl l-то же самое, вызванное неизвестным моментом X. Для определения CPLP и Yax используется графоаналитический метод. Согласно этому способу угол поворота поперечного сечения действительной балки численно равен величине поперечной силы, найденной в том же поперечном сечении фиктивной балки. График основного момента
системы(рис. 278 от силы Р и неизвестного х, а) показано на рисунке. 278b C из этих результатов, накладные балки, подвергнутые накладной нагрузке, соответственно, могут быть показаны на рисунке. 278, г и Д. Чтобы определить мнимую боковую силу левого опорного сечения, значения L1F и a^f(рис. 278, г и г). Из уравнений статики мы имеем (см. диаграмму. 278, г.): . 1 / o s-E,] 3 » B1F-6E/’ ‘•- Т’ —
- }- S1f- 2/ — 0 я не уверен. Если вы присваиваете значение 1F, это выглядит следующим образом: — — Ми’/ ‘2 4Е / 2 ‘ 1t2W2 s=0; — S2f-/2>o = °>D2f. -о-с — ^2- 2Ф » 16E7″ / — С 2f-2 / = — 0. Подставляя значение C2F, находим(см. диаграмму. 278, д.) В Р12 ^ 2Ф-16Э/ • Поскольку угол поворота поперечного сечения действительной балки численно равен поперечной силе воображаемой балки, получаем: _d_XI. Ф л ч~l1F~е/ ‘ Я_ _ П12 U AR-L2F-1 6E / • Назначьте значения в выражении X1_o-X-P1 16Э/+Е/—16 • 315I Данная система —* Основная система/ Шесть.)
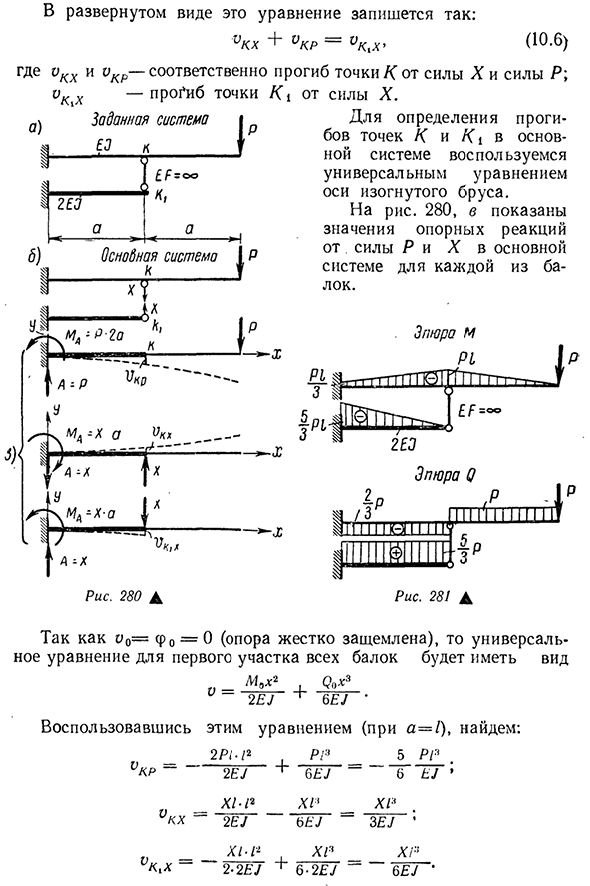
Вариант 1 Отчет- Ноль. ₽ ₽ / ₽ Два.) Икс Вариант 3 — … Отчет—— В Вариант 2 … Отчет—— В I » Рис. 277D Но) 1. Иды’ По< / П ; Участок MX W x / b — ^gtgp^Ggrtt^ Рис 278D После определения избыточного неизвестного X из уравнения B/2статики находим опорные реакции A, B и C(рис. 279, а): 2^=0; _L/+H=0; L=4″= 2 » >W=0; — L- 2 / + — 4 + — 4 — C1=0. 2У=.О; — Л+Б+В-Р=0; Б=Р+Л-С=Р+4—^Р=4-Р. Затем создайте окончательный график момента и боковых сил в нормальном порядке(рис. 279, б). Для определения угла отклонения и поворота сечения этой балки можно также использовать метод графического анализа. П р и М Е Р2.
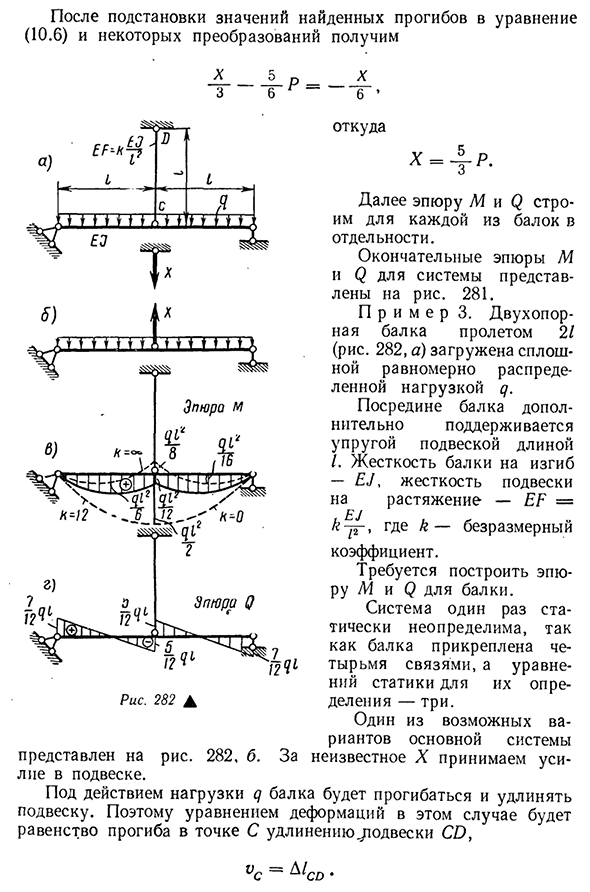
Эта система состоит из двух плотно защемленных на левом конце балки, абсолютно жестких Людмила Фирмаль
(недеформируемых) шарнирных соединений к — /С1 (рис. 280, а). Жесткость верхней балки-е^, нижней-2е/. Вам нужно построить участок M и F. один из простейших вариантов базовой системы показан на рисунке. 280, б. Поскольку связь / C-K предполагается абсолютно жесткой, то отклонение точки K вследствие действия внешней силы P будет таким же, как и отклонение точки/CP, поэтому уравнение деформации в этом случае не корректно. 317 это выражение записывается следующим образом: ^Ч■+■11CR==(10.6) Где AK x и^ — отклонение точки K от силы X и силы P соответственно. Для определения прогиба точек K и K1 основной системы используют
универсальное уравнение оси криволинейной балки. Для риса. 280, б показаны значения опорных реакций сил Р и Х в основной системе каждого пучка. Участок М Рис, 281а. ^0=384E7’s x48E/ ‘X ER’ П Подставив значения VC, VC x и D/x в уравнение (10.7), получим следующее уравнение: 4+т 16 / 4х * 8 / 3_X и3 384EL48E7 » Кэл Решение этого уравнения имеет вид Икс — 5d1 (10.8) 1. — Двадцать четыре Подумайте о 3 случаях:1)&=0. Тогда из Формулы(10.8) получим X=0.
Сюжет момента в этом случае показан на рисунке. 282, пунктиром; 2) K=OO. Из равенства (10.8) Х= — Н1. Четыре. В этом случае подвеска превращается в жесткую шарнирную опору. Сюжет момента такого луча состоит из цифр. 273, E. Этот участок обозначен пунктирной линией на рисунке. 282, в;3) к-12. Из равенства (10.8) Х= -<?/. Шесть. Мы построим эпюры M и F для простой поддержки Бол-5 Ки загружена нагрузки<7 и Х=-^ — д/. Графики M и f, когда K-12 показан на рисунке. 282, В и Д.
Смотрите также:

